通过文章主题做文本分类的理论依据
直观来讲,如果一篇文章有一个中心思想,那么一些特定词语会更频繁的出现。比方说,如果一篇文章是在讲猫的,那"猫"和"鱼"等词出现的频率会高些,如果一篇文章是在讲狗的,那"狗"和"骨头"等词出现的频率会高些。而有些词例如"这个"、"和"大概在两篇文章中出现的频率会大致相等。但真实的情况是,一篇文章通常包含多种主题,而且每个主题所占比例各不相同。因此,如果一篇文章10%和猫有关,90%和狗有关,那么和狗相关的关键字出现的次数大概会是和猫相关的关键字出现次数的9倍。
- 由于上面的理论基础,在文本分析中就有了基于文章主题的分类方法。
主题模型是用来在一系列文档中发现抽象主题(topic)的一种统计模型(在机器学习PAI平台,我们给PLDA组件设置topic参数值为50,表示让每篇文章抽象出50个主题)。
主题模型核心思想:数学框架(统计+概率)
主题模型试图用数学框架来体现文档的这种特点。主题模型自动分析每个文档,统计文档内的词语,根据统计的信息来断定当前文档含有哪些主题,以及每个主题所占的比例各为多少。
- 下面说一种最经典的主题模型-LDA(隐含狄利克雷分布)
LDA(Latent Dirichlet allocation),是一种主题模型,它可以将[文档集]中每篇文档的主题按照概率分布的形式给出,从而通过分析一些文档抽取出它们的主题,然后根据主题给文本分类。它是一种无监督学习算法,在训练时不需要手工标注的训练集,需要的仅仅是文档集以及指定主题的数量k(这个K就是PLDA参数topic)即可。
- 目前机器学习PAI平台文本分析组件PLDA,它是Google对LDA的开源实现。
语料生成过程(语料就是我们需要分析的所有文本,即文本集)
假设语料库中有M篇文档(在这里我们定义:z是主题, w是词, d是文档),其中W(m)表示第m篇文档中的词,Z(m)表示这些词对应的topic编号。所有的word和对应的topic如下表示:
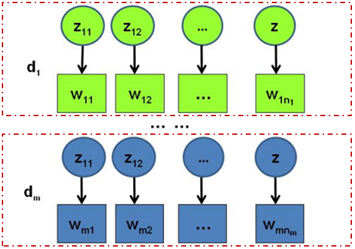
红色方框内即表示一篇文档是由若干个词组成的,每个词都对应一个主题。(就像一篇文章所有的词都是为了更好的表达主题而存在的)
- 下面我们思考当写一篇文章时你是怎么做的。
假设你要写一篇文章,首先想好了主题(一个或多个),然后围绕这几个主题(比如"Arts""Budgets""Children""Education")你会想到很多与之相关的词:
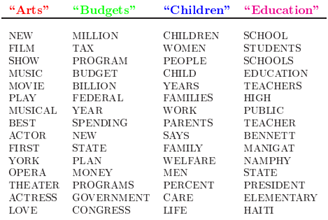
最后我们就是用这些和主题相关的词完成了一篇文章,就像下图一样,不同的颜色代表不同主题下的词,从颜色能看出每个主题的下面的词出现概率是不相同的:

上面的这个案例是我们在确定主题和词之后生成文章的步骤。然后伟大的数学家把这个过程抽象成了概率分布问题(关于如何抽象,当然是一大堆假设和公式推导,最后得出结论)
生成这篇文章可以看作如下过程:
首先以一定的概率在"Arts"、"Budgets"、"Children"、"Education"中选择一个主题
然后再以一定的概率在这个主题下选择某个单词
不断重复以上两个步骤,最终完成一篇文章
这里的两次"以一定的概率",后面会有解释。
- 通过上面的分析,我们知道了文章生成过程,下来来说LDA模型
《LDA数学八卦》中把文档生成过程抽象成了一个游戏,主要是为了解决刚才我们说的"以一定概率"的问题。上帝有两种类型骰子:

上面红框里面内容是说,每个doc-topic骰子是一篇文章的所有主题。
上帝在LDA模型中,玩文档生成游戏的规则是这样的:

这个文档生成规则可以看作如下过程:
首先上帝有两大坛骰子
第一坛装的是doc-topic骰子,就是和所有文档相关的所有主题;
第二坛装的是topic-word骰子,就是和所有主题相关的所有单词;
开始文档生成游戏
随机从topic-word坛子独立抽取K个骰子,编号为1,2,3…k
随机从doc-topic坛子抽取一个骰子,然后重复如下过程生成文档中的词:
投掷doc-topic骰子,得到一个topic编号z
投掷刚才K个骰子中选择编号为z的那个骰子,得到一个词
每次都是先生成一篇文档之后再生成第二篇,文档中每个词的生成都要投掷两次骰子,第一次投掷doc-topic骰子得到一个topic,第二次投掷topic-word骰子得到一个word,就是说生成文档中的一个词要投掷2次。如果语料中有N个词,那么上帝要抛2N次,轮换抛doc-topic和topic-word。实际上一些投掷顺序是可以交换的(这里有很多公式推导,最终得到这个顺序可以交换),我们可以等价交换这2N次投掷顺序,先抛N次doc-topic骰子,得到语料中所有词的topic,然后基于每个topic的编号,再抛N次topic-word骰子得到语料中所有word。
于是上帝的游戏规则就变成了这样:

这个过程是这样的:
随机从topic-word坛子独立抽取K个骰子,编号为1,2,3…k
随机抽取一个doc-topic骰子,然后抛出得到一个主题z,再次抽取doc-topic骰子,再抛出,得到一个主题z(注意:由于是再次抽取,所以不一定还是之前那篇文档的主题);重复这个步骤就能得到语料中所有文档主题
从头到尾抛我们抽到的doc-topic骰子,从最开始抽到的topic-word骰子中取相应编号(在1到k中拿)的骰子抛出,得到对应的word
以面的过程是先生成了语料中所有的topic,然后生成了所有的word。在topic生成的情况下word顺序是可以交换的,即如果确定了topic k,就算和它相关的word不在同一篇文章中,也是可以交换的。
...数学家们做了假设和分析,搞懂了原理,他们决定把这些用公式表示,于是就算啊算,用到了贝叶斯、Dirichlet-Multionmial共轭结构、Gibbs-Sampling采样(一堆公式)最终...
牛X的数学家(神)得到了一个公式:
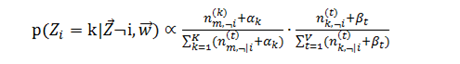
这里面z,i,k,t,v,m...只要知道都是一系列参数就行,比如文档编号、topic编号、word编号、第k个topic产生的词中word t的个数、文章数量...
这个公式右边就是p(topic|word)*p(word|topic),概率就是doc-->topic-->word的路径概率:
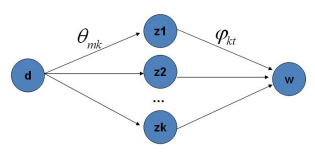
接下来任务有两个:

这里用到了Gibbs-Sampling公式,它的意义就是在k条路径中采样,基于语料训练LDA模型,模型中参数可以基于采集到的样本进行评估(我们做这些都是为了得到上面式子的参数)。
下面是训练过程:

由这个topic-word频率矩阵我们可以计算出每一个p(word|topic)概率。
Gibbs-Sampling收敛后统计每篇文档中topic的频率分布就可以计算出p(topic|doc)的概率。(PAI平台PLDA组件有六个输出桩后面会解释)
LDA的核心公式如下:
P(word|doc)=p(word|topic)*p(topic|doc)
通过计算可以得到任意一个topic对应文档d中单词w出现的概率,通过这个概率不断修正我们的参数。
- 有了模型,接下来做的就是对于新来的文档doc(new)计算topic语义分布。
下面是具体计算过程:

迭代过程即:首先产生一个均匀分布的随机数,然后根据上式计算每个转移主题的概率,通过累积概率判断随机数落在哪个new topic下,更新参数矩阵,如此迭代直至收敛。
-
回到我们机器学习PAI,先看下PLDA模块的6个输出桩
-
输出桩1:词频,算法内部抽样后每个词在主题出现次数
-
输出桩2:P(单词|主题)每个主题下词的概率
-
输出桩3:P(主题|单词)每个单词对应各个主题的概率
-
输出桩4:P(文档|主题)每个主题对应各个文档的概率
-
输出桩5:P(主题|文档)每个文档对应主题的概率
-
输出桩6:P(主题)每个主题的概率,表明在整个文档中的权重
通过上面的公式推导,计算出关键的几个概率,通过贝叶斯公式这几个值都是可以算出来的。
第5个是输出桩输出结果显示的是每篇文章对应的每个主题的概率,而这个概率在上面通过p(topic|doc)已经算出。
在实验中我们设置参数topic=50,这个主题数是相对整个语料库而言的,我们最后看到的结果是这50个主题在每一篇文章上的分布情况。其它默认即可。对于默认的几个参数给予功能性的说明:



我们将文章id列和主题概率分布列,得到每个主题在每篇文章的概率分布如下图所示:
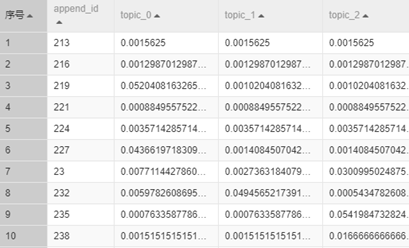
上面把文章从主题的维度表示成了一个向量。接下来就可以通过向量的距离实现聚类,从而实现文章分类。
关于是如何聚类的下一篇文章会给详细解释过程。