- 矩阵定义
1 Matrix<double, 3, 3> A; // A.定义3x3double 矩阵 2 Matrix<double, 3, Dynamic> A; //定义3xn double 矩阵,列为动态变化 3 Matrix<double, Dynamic, Dynamic> A; // 定义 double 矩阵,行、列为动态变化,由需要决定 4 MatrixXd A; // 定义 double 矩阵,行、列为动态变化,由需要决定 5 Matrix<double, 3, 3, RowMajor> A; // 定义3x3 double 矩阵,按行储存,默认按列储存效率较高。 6 Matrix3f A; // 定义3x3 float 矩阵A. 7 Vector3f A; // 定义3x1 float 列向量A. 8 VectorXd A; // 定义动态double列向量A 9 RowVector3f A; // 定义1x3 float 行向量A. 10 RowVectorXd A; // 定义动态double行向量A.
- 矩阵使用
- 赋值
Matrix<double, 3, 3> A; A << 1, 2, 3, 4, 5, 6, 7, 8, 9;
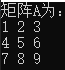
1 RowVectorXd vec1(3); 2 vec1 << 1, 2, 3; 3 4 RowVectorXd vec2(4); 5 vec2 << 1, 4, 9, 16; 6 7 RowVectorXd joined(7); 8 joined << vec1, vec2; 9
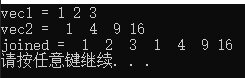
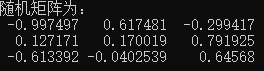
MatrixXd A = MatrixXd::Random(3, 3); //随机生成3*3的double型矩阵
1 Matrix3d A= Matrix3d::Zero(); //生成3*3的0矩阵
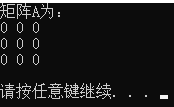
Matrix3d A; A.fill(3);//全部为3
Matrix3d A;
A.fill(3);
Matrix<double, 3,9> B;
B << A, A, A; //按块添加
- 操作元素
1 // Basic usage 2 // Eigen // Matlab // comments 3 x.size() // length(x) // vector size 4 C.rows() // size(C,1) // number of rows 5 C.cols() // size(C,2) // number of columns 6 x(i) // x(i+1) // Matlab is 1-based 7 C(i, j) // C(i+1,j+1) // 8 9 A.resize(4, 4); // Runtime error if assertions are on. 10 B.resize(4, 9); // Runtime error if assertions are on. 11 A.resize(3, 3); // Ok; size didn't change. 12 B.resize(3, 9); // Ok; only dynamic cols changed. 13 14 A << 1, 2, 3, // Initialize A. The elements can also be 15 4, 5, 6, // matrices, which are stacked along cols 16 7, 8, 9; // and then the rows are stacked. 17 B << A, A, A; // B is three horizontally stacked A's. 18 A.fill(10); // Fill A with all 10's.
1 Matrix<double, 3, 2> A; 2 A << 1, 2, 3 3, 7, 4 8, 9; 5 cout << "矩阵A为:" << endl << A << endl 6 << "矩阵A的元素个数为:" << A.size() << endl 7 << "矩阵A的行数为:" << A.rows() << endl 8 << "矩阵A的列数为:" << A.cols() << endl 9 << "矩阵A的第4个元素为:" << A(3) << endl //按列存储,左列为0-2右列为3-5 10 << "矩阵A的第2行第2列元素为:" << A(1, 1) << endl;//行列从0开始

-
- 特殊矩阵:
1 // Eigen // Matlab 2 MatrixXd::Identity(rows,cols) // eye(rows,cols) 3 C.setIdentity(rows,cols) // C = eye(rows,cols) 4 MatrixXd::Zero(rows,cols) // zeros(rows,cols) 5 C.setZero(rows,cols) // C = ones(rows,cols) 6 MatrixXd::Ones(rows,cols) // ones(rows,cols) 7 C.setOnes(rows,cols) // C = ones(rows,cols) 8 MatrixXd::Random(rows,cols) // rand(rows,cols)*2-1 // MatrixXd::Random returns uniform random numbers in (-1, 1). 9 C.setRandom(rows,cols) // C = rand(rows,cols)*2-1 10 VectorXd::LinSpaced(size,low,high) // linspace(low,high,size)' 11 v.setLinSpaced(size,low,high) // v = linspace(low,high,size)'
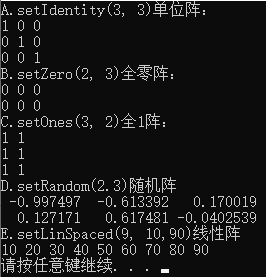
实例操作:
1 MatrixXd A,B,C,D; 2 Matrix<double, 1, 9> E; 3 cout << "A.setIdentity(3, 3)单位阵:" << endl << A.setIdentity(3, 3) << endl//单位阵 4 << "B.setZero(2, 3)全零阵:" << endl << B.setZero(2, 3) << endl//全零矩阵 5 << "C.setOnes(3, 2)全1阵:" << endl << C.setOnes(3, 2) << endl//全1矩阵 6 << "D.setRandom(2.3)随机阵" << endl << D.setRandom(2, 3) << endl//随机阵 7 << "E.setLinSpaced(9, 10,90)线性阵" << endl << E.setLinSpaced(9, 10,90) << endl;//线性阵9个数10-90均匀分布
矩阵分块:
// 下面x为列或行向量,P为矩阵 // Eigen // Matlab x.head(n) // x(1:n) x.head<n>() // x(1:n) x.tail(n) // x(end - n + 1: end) x.tail<n>() // x(end - n + 1: end) x.segment(i, n) // x(i+1 : i+n) x.segment<n>(i) // x(i+1 : i+n) P.block(i, j, rows, cols) // P(i+1 : i+rows, j+1 : j+cols) P.block<rows, cols>(i, j) // P(i+1 : i+rows, j+1 : j+cols) P.row(i) // P(i+1, :) P.col(j) // P(:, j+1) P.leftCols<cols>() // P(:, 1:cols) P.leftCols(cols) // P(:, 1:cols) P.middleCols<cols>(j) // P(:, j+1:j+cols)//取出从j+1列开始的cols列 P.middleCols(j, cols) // P(:, j+1:j+cols) P.rightCols<cols>() // P(:, end-cols+1:end) P.rightCols(cols) // P(:, end-cols+1:end) P.topRows<rows>() // P(1:rows, :) P.topRows(rows) // P(1:rows, :) P.middleRows<rows>(i) // P(i+1:i+rows, :) P.middleRows(i, rows) // P(i+1:i+rows, :) P.bottomRows<rows>() // P(end-rows+1:end, :) P.bottomRows(rows) // P(end-rows+1:end, :) P.topLeftCorner(rows, cols) // P(1:rows, 1:cols) P.topRightCorner(rows, cols) // P(1:rows, end-cols+1:end) P.bottomLeftCorner(rows, cols) // P(end-rows+1:end, 1:cols) P.bottomRightCorner(rows, cols) // P(end-rows+1:end, end-cols+1:end) P.topLeftCorner<rows,cols>() // P(1:rows, 1:cols) P.topRightCorner<rows,cols>() // P(1:rows, end-cols+1:end) P.bottomLeftCorner<rows,cols>() // P(end-rows+1:end, 1:cols) P.bottomRightCorner<rows,cols>() // P(end-rows+1:end, end-cols+1:end)
实例操作:
1 Matrix<double, 3, 3> A; 2 A << 1, 2, 3, 3 4, 5, 6, 4 7, 8, 9; 5 Vector4d B;//列向量 6 B << 1, 2, 3, 4; 7 RowVector4f C;//行向量 8 C << 0, 1, 2, 3; 9 cout << "矩阵A为:" << endl << A << endl 10 << "列向量B为:" << endl << B << endl 11 << "行向量C为:" << endl << C << endl 12 << "列向量B的前2个元素B.head(2)为:" << endl << B.head(2) << endl 13 << "行向量C的前2个元素C.head<2>()为:" << endl << C.head<2>() << endl 14 << "列向量B的倒数2个元素B.tail(2)为:" << endl << B.tail(2) << endl 15 << "行向量C的倒数2个元素C.tail<2>()为:" << endl << C.tail<2>() << endl 16 << "获取从列向量B的第0个元素开始的2个元素B.segment(0, 2):" << endl << B.segment(0, 2) << endl 17 << "获取从行向量C的第1个元素开始的3个元素C.segment<3>(1):" << endl << C.segment<3>(1) << endl 18 /* 分块矩阵 */ 19 << "矩阵A的前两行中间列元素A.block(0, 1, 2, 1):" << endl << A.block(0, 1, 2, 1) << endl 20 << "矩阵A的前两行中间列元素A.block<2, 1>(0, 1):" << endl << A.block<2, 1>(0, 1) << endl 21 << "矩阵A的第二行元素A.row(1):" << endl << A.row(1) << endl 22 << "矩阵A的第二列元素A.col(1):" << endl << A.col(1) << endl 23 << "矩阵A的左边两列元素A.leftCols<2>():" << endl << A.leftCols<2>() << endl 24 << "矩阵A的左边一列元素A.leftCols(1):" << endl << A.leftCols(1) << endl 25 << "矩阵A的第二列第三列元素A.middleCols<2>(1):" << endl << A.middleCols<2>(1) << endl 26 << "矩阵A的第二列元素A.middleCols(1, 1):" << endl << A.middleCols(1, 1) << endl 27 << "矩阵A的左上角两行两列元素A.topLeftCorner(2, 2):" << endl << A.topLeftCorner(2, 2) << endl;


矩阵元素交换:
// Eigen // Matlab R.row(i) = P.col(j); // R(i, :) = P(:, i) R.col(j1).swap(mat1.col(j2)); // R(:, [j1 j2]) = R(:, [j2, j1])
矩阵转置:
1 // Eigen // Matlab 2 R.adjoint() // R' 3 R.transpose() // R.' or conj(R') 4 R.diagonal() // diag(R) 5 x.asDiagonal() // diag(x) 6 R.transpose().colwise().reverse(); // rot90(R) 7 R.conjugate() // conj(R)
矩阵乘积:
// Matrix-vector. Matrix-matrix. Matrix-scalar. y = M*x; R = P*Q; R = P*s; a = b*M; R = P - Q; R = s*P; a *= M; R = P + Q; R = P/s; R *= Q; R = s*P; R += Q; R *= s; R -= Q; R /= s;
矩阵内部元素操作:
// Vectorized operations on each element independently // Eigen // Matlab R = P.cwiseProduct(Q); // R = P .* Q R = P.array() * s.array();// R = P .* s R = P.cwiseQuotient(Q); // R = P ./ Q R = P.array() / Q.array();// R = P ./ Q R = P.array() + s.array();// R = P + s R = P.array() - s.array();// R = P - s R.array() += s; // R = R + s R.array() -= s; // R = R - s R.array() < Q.array(); // R < Q R.array() <= Q.array(); // R <= Q R.cwiseInverse(); // 1 ./ P R.array().inverse(); // 1 ./ P R.array().sin() // sin(P) R.array().cos() // cos(P) R.array().pow(s) // P .^ s R.array().square() // P .^ 2 R.array().cube() // P .^ 3 R.cwiseSqrt() // sqrt(P) R.array().sqrt() // sqrt(P) R.array().exp() // exp(P) R.array().log() // log(P) R.cwiseMax(P) // max(R, P) R.array().max(P.array()) // max(R, P) R.cwiseMin(P) // min(R, P) R.array().min(P.array()) // min(R, P) R.cwiseAbs() // abs(P) R.array().abs() // abs(P) R.cwiseAbs2() // abs(P.^2) R.array().abs2() // abs(P.^2) (R.array() < s).select(P,Q); // (R < s ? P : Q)
矩阵化简:
// Reductions. int r, c; // Eigen // Matlab R.minCoeff() // min(R(:)) R.maxCoeff() // max(R(:)) s = R.minCoeff(&r, &c) // [s, i] = min(R(:)); [r, c] = ind2sub(size(R), i); s = R.maxCoeff(&r, &c) // [s, i] = max(R(:)); [r, c] = ind2sub(size(R), i); R.sum() // sum(R(:)) R.colwise().sum() // sum(R) R.rowwise().sum() // sum(R, 2) or sum(R')' R.prod() // prod(R(:)) R.colwise().prod() // prod(R) R.rowwise().prod() // prod(R, 2) or prod(R')' R.trace() // trace(R) R.all() // all(R(:)) R.colwise().all() // all(R) R.rowwise().all() // all(R, 2) R.any() // any(R(:)) R.colwise().any() // any(R) R.rowwise().any() // any(R, 2)
矩阵点乘
// Dot products, norms, etc. // Eigen // Matlab x.norm() // norm(x). Note that norm(R) doesn't work in Eigen. x.squaredNorm() // dot(x, x) Note the equivalence is not true for complex x.dot(y) // dot(x, y) x.cross(y) // cross(x, y) Requires #include <Eigen/Geometry>
矩阵类型转换:
//// Type conversion // Eigen // Matlab A.cast<double>(); // double(A) A.cast<float>(); // single(A) A.cast<int>(); // int32(A) A.real(); // real(A) A.imag(); // imag(A) // if the original type equals destination type, no work is done
求解线性方程组Ax=b
// Solve Ax = b. Result stored in x. Matlab: x = A b. x = A.ldlt().solve(b)); // A sym. p.s.d. #include <Eigen/Cholesky> x = A.llt() .solve(b)); // A sym. p.d. #include <Eigen/Cholesky> x = A.lu() .solve(b)); // Stable and fast. #include <Eigen/LU> x = A.qr() .solve(b)); // No pivoting. #include <Eigen/QR> x = A.svd() .solve(b)); // Stable, slowest. #include <Eigen/SVD> // .ldlt() -> .matrixL() and .matrixD() // .llt() -> .matrixL() // .lu() -> .matrixL() and .matrixU() // .qr() -> .matrixQ() and .matrixR() // .svd() -> .matrixU(), .singularValues(), and .matrixV()
矩阵特征值:
// Eigenvalue problems // Eigen // Matlab A.eigenvalues(); // eig(A); EigenSolver<Matrix3d> eig(A); // [vec val] = eig(A) eig.eigenvalues(); // diag(val) eig.eigenvectors(); // vec // For self-adjoint matrices use SelfAdjointEigenSolver<>