问题描述
给你一个非零整数,让你求这个数的n次方,每次相乘的结果可以在后面使用,求至少需要多少次乘。如24:2*2=22(第一次乘),22*22=24(第二次乘),所以最少共2次;
输入格式
第一行m表示有m(1<=m<=100)组测试数据;
每一组测试数据有一整数n(0<n<=100000000);
每一组测试数据有一整数n(0<n<=100000000);
输出格式
输出每组测试数据所需次数s;
样例输入
3
2
3
4
2
3
4
样例输出
1
2
2
2
2
看半天也没看明白"给你一个非零整数,让你求这个数的n次方",中的"这个数"是谁,不过好像没影响,暂定输入的数是"这个数",也是要求的次方数。
分析样例:
输入2时,求2^2从2由几步能得出:2 * 2 = 2^2,一步得出
输入3时,求3^3从3由几步能得出:3 * 3 = 3^2,3^2 * 3 = 3^3,两步得出
输入4时,求4^4从4由几步能得出:4 * 4 = 4^2,4^2 * 4^2 = 4^4,两步得出
先看代码再解释
1 #include <bits/stdc++.h> 2 using namespace std; 3 int main() { 4 int t; 5 cin >> t; 6 while (t--) { 7 int n; 8 cin >> n; 9 int ans = 0; 10 while (n != 1) { 11 if(n % 2 != 0) { //奇数,乘两次 12 ans += 2; 13 } else { //偶数,乘一次 14 ans++; 15 } 16 n /= 2; 17 } 18 cout << ans << endl; 19 } 20 return 0; 21 }
解释:从大向小递归分析,
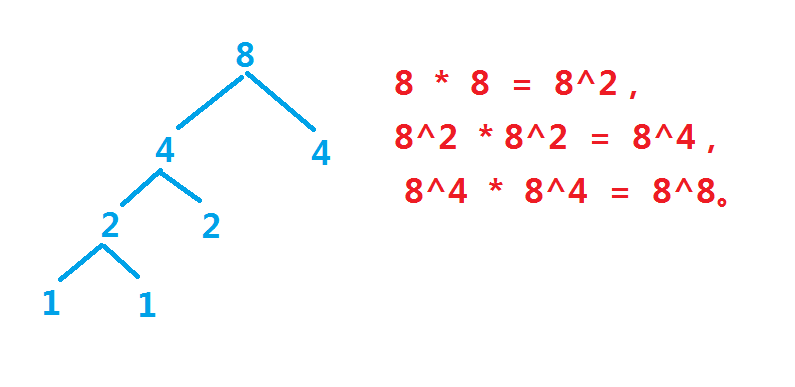
当n=8时,要求8次方能由几步乘法得出,8是偶数,n / 2 = 4,8次方可以由4次方乘4次方得出,需要一步
然后分析4次方能由几步乘法得出,相当于上一步中的n现在变为n=4了,n / 2 = 2,4次方可以由2次方乘2次方得出,又需要一步
然后分析2次方能由几步乘法得出,相当于上一步中的n现在变为n=2了,n / 2 = 1,2次方可以由1次方乘1次方得出,又需要一步
要求8^8,一共需要3步,8 * 8 = 8^2,8^2 * 8^2 = 8^4, 8^4 * 8^4 = 8^8。
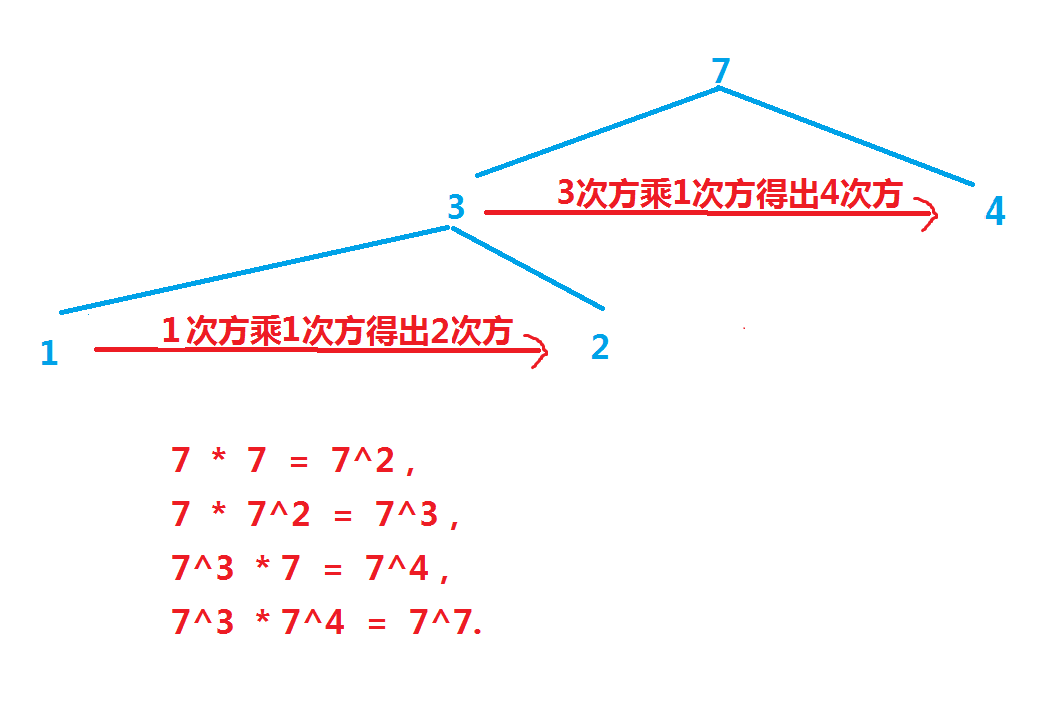
当n=7时,要求7次方能由几步乘法得出,7是奇数,n / 2 = 3(c++里除法向下取整),7次方可以由3次方乘4次方得出,就是说,我们先得出3次方,然后3次方乘以1次方,得出4次方。再拿3次方乘以4次方得出7次方,需要两步
然后分析3次方能由几步乘法得出(因为上一步中的4次方是由3次方乘以1次方得出的,这里只需要考虑得出3次方需要几步),相当于上一步中的n现在变为n=3了,n / 2 = 1,3次方可以由1次方乘2次方得出,2次方是由1次方乘以1次方得出,又需要两步
所以要求7^7,一共需要4步,7 * 7 = 7^2,7 * 7^2 = 7^3, 7 ^ 3 * 7 = 7^4,7^3 * 7^4 = 7^7.