
对应到c++容器是优先队列
优先队列做法
1 #include <bits/stdc++.h> 2 using namespace std; 3 int main() { 4 int n, m; 5 cin >> n >> m; 6 priority_queue<int, vector<int>, greater<int> > q; 7 //升序队列 8 //priority_queue <int,vector<int>,greater<int> > q; 9 //降序队列 10 //priority_queue <int,vector<int>,less<int> >q; 11 for (int i = 1; i <= n; i++) { 12 int t; 13 cin >> t; 14 q.push(t); 15 } 16 while (m--) { 17 cout << q.top() << " "; 18 q.pop(); 19 } 20 return 0; 21 }
手写堆做法:
前三个功能是stl里的堆支持的基本操作
后面两个操作是stl里的堆无法直接实现,也就是说没有一步到位的函数支持
先讲一下堆的基本结构
堆是一个完全二叉树, 除了最后一层,上面所有节点都是满的,最后一层的叶子节点是从左到右排列

堆又有大根堆和小根堆
以小根堆为例:每一个点都是小于等于左右儿子的,所以根节点就是整个树的最小值
堆的存储:用一维数组存储,1号点是根节点
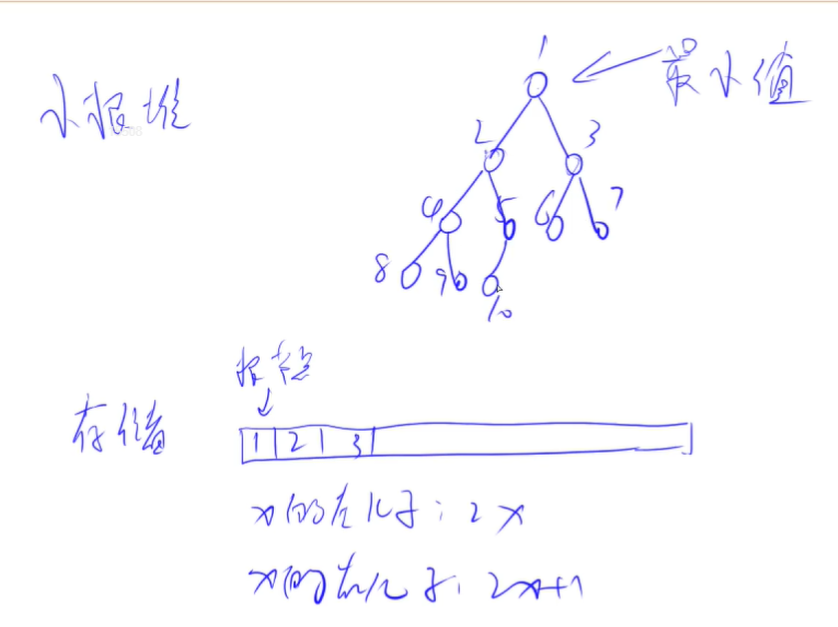
堆有两个基本操作
up():将一个节点往上移和down():将一个节点往下移
上面提到的5个操作都可以用这两个函数实现
down(x)函数 { //如果把某一个点变大了,需要把它往下移
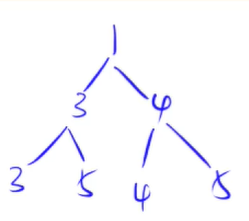
将最上面的1换为6之后,然后6应该咋样移动到它应该在的位置
在x点,和x点的两个儿子(如果有的话),一共最多三个点中找到一个最小值min
交换x和min的位置
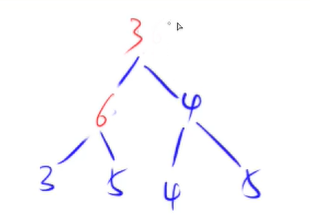
然后递归处理

当交换到不能交换时,整个树更新为一个新的堆
}
up() { //如果把某一个点变小了,需要把它往上移
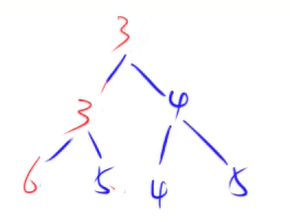
如果把右下角的5改为2

只需要把变的这个点和根节点进行比较

然后递归处理

}
用se表示当前堆的大小
用heap[]数组表示堆

up操作和down操作的时间复杂度和树的高度成正比,都是log n
在建堆操作时,我们是从下往上递归的,所以可以保证两个儿子都是堆
1 #include <bits/stdc++.h> 2 using namespace std; 3 const int N = 100010; 4 int h[N], se; 5 void down(int u) { 6 int t = u; //用t来表示这三个点的最小值 7 if (2 * u <= se && h[2 * u] < h[t]) { //如果有左儿子,并且左儿子更小的话 8 t = 2 * u; 9 } 10 if (2 * u + 1 <= se && h[2 * u + 1] < h[t]) { //如果有右儿子,并且右儿子更小的话 11 t = 2 * u + 1; 12 } 13 if (u != t) { //如果根节点不是最小值 14 swap(h[u], h[t]); 15 down(t); 16 } 17 } 18 void up(int u) { 19 while (u / 2 > 0 && h[u / 2] > h[u]) { //只要有父节点,并且父节点比我大 20 swap(h[u / 2], h[u]); 21 u /= 2; 22 } 23 } 24 int main() { 25 int n, m; 26 cin >> n >> m; 27 for (int i = 1; i <= n; i++) { 28 cin >> h[i]; 29 } 30 se = n; 31 for (int i = n / 2; i > 0; i--) { //O(n)的建堆方式 32 //cout << i << endl; 33 down(i); 34 } 35 while (m--) { 36 cout << h[1] << " "; 37 h[1] = h[se]; 38 se--; 39 down(1); 40 } 41 return 0; 42 }