16.字符串哈希 哈希表

 

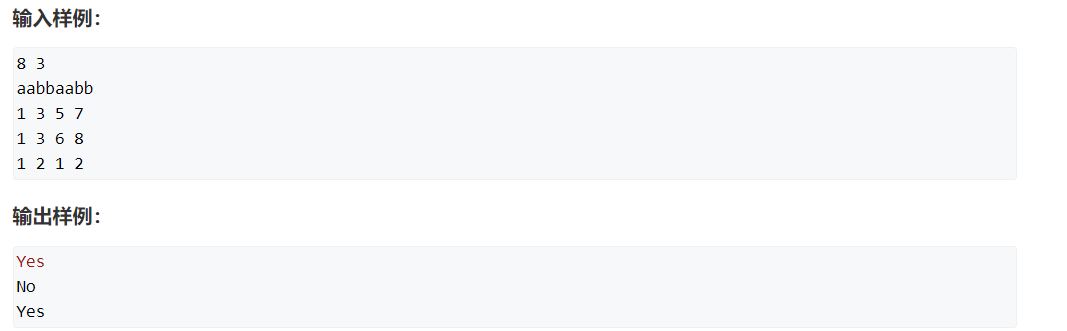
 这个方法叫做字符串前缀哈希法- -

先求出来每个前缀的哈希值

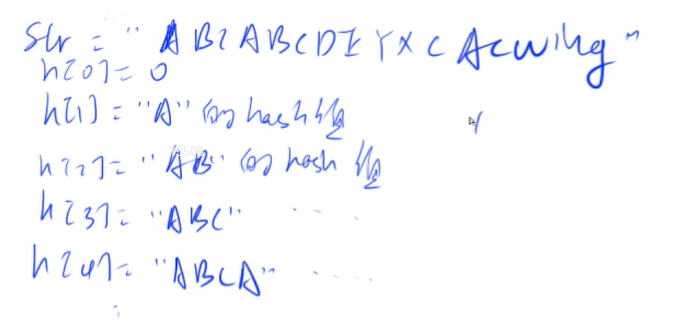
 问题1：如何来定义某一个前缀的哈希值

把这个字符串看成是一个P进制的数

每一位上的字母的ascii码，就是这一位上的数

 最后mod上一个很小的数，就映射到0 ~ Q - 1

这样就可以把一个字符串转换为一个数字

注意事项1：

一般情况下，不能把某个字母映射成0

比如把A映射成0

那A，AA，AAA都是0了。这样就把不同的字符串映射成同样的数字了，错误

注意事项2：

之前的哈希方式是有处理冲突的机制的

这里我们是假定不会有冲突的

 从数学结论上看，在P = 131 或13331，Q = 2 ^ 64的情况下

在99.99%的情况下，不会有冲突

至于为啥不会有冲突，这个就好比常见取模数是1000000001，1000000003，1000000007。可以直接记下来

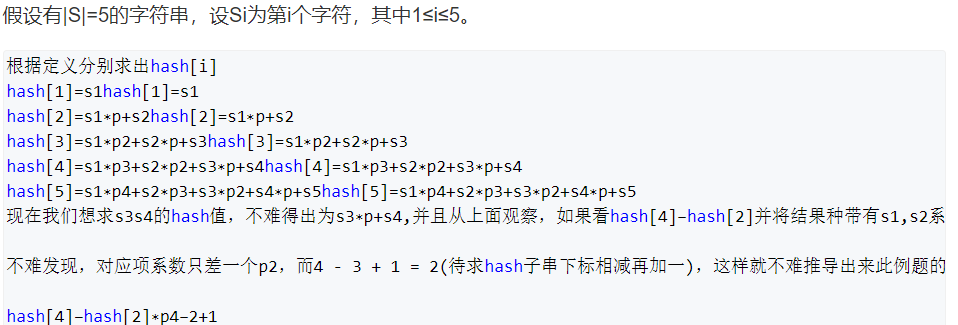
 问题2：这样的哈希方式再配合上前缀哈希，有啥好处

好处就是可以利用前缀哈希，计算出来每一个子串的哈希值。前缀和思想，万物皆可前缀和

 [L, R]的哈希值就可以用公式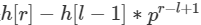计算出来

 我们直接用unsigned long long来存储所有的h[]

这样就不用对2 ^ 64取模了，溢出就等价于取模

预处理h[]数组直接用

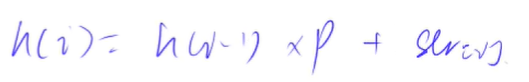
  只要s[i]不是0就可以

#include <bits/stdc++.h>
using namespace std;
const int N = 100010, P = 131;
char s[N];
typedef unsigned long long ULL;
ULL h[N], p[N];
//p数组用来存储p的多少次方
ULL get(int l, int r) {
    return h[r] - h[l - 1] * p[r - l + 1];
}
//哈希值是0 ~ 2 ^ 64 - 1之间的一个数
int main() {
    int n, m;
    cin >> n >> m >> s + 1;
    p[0] = 1; //p的0次方等于1
    for (int i = 1; i <= n; i++) { //从第一个字母开始
        p[i] = p[i - 1] * P;
        h[i] = h[i - 1] * P + s[i];
    }
    while (m--) {
        int l1, r1, l2, r2;
        cin >> l1 >> r1 >> l2 >> r2;
        if (get(l1, r1) == get(l2, r2)) {
            cout << "Yes" << endl;
        } else {
            cout << "No" << endl;
        }
    }
    return 0;
}