
树和图有两种存储方式,树是一种特殊的图,树是无环连通图
图分为有向图和无向图,无向图是一种特殊的有向图

所以就只需要考虑有向图怎样存储
有向图的存储有两大类
第一大类是用得比较少的邻接矩阵,就是开个二维数组g[a][b]存储a到b这条边的信息,这条边有权重就记录权重,没权重就记录这条边是否存在,0或1
邻接矩阵是不能存储重边的,只能存储一条(权重最小)的边
领接矩阵比较浪费空间,空间复杂度n ^ 2,适合存储稠密图
第二大类是用得最多的邻接表
邻接表就是之前的单链表。如果有n个点的话,就开n个单链表。
和拉链法的哈希表一样
每个点上的单链表存储这个点可以到哪个点去
举个例子
比如有一个这样的图
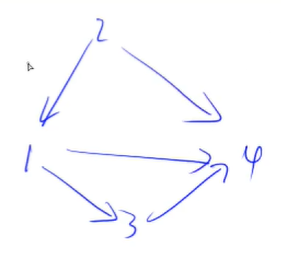
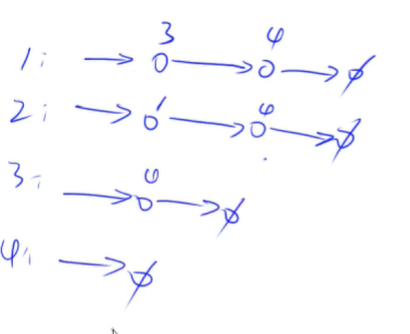
然后如何用单链表存储上面这个图呢
因为有4个点,所以就开4个单链表
单链表内部每个点的次序无所谓
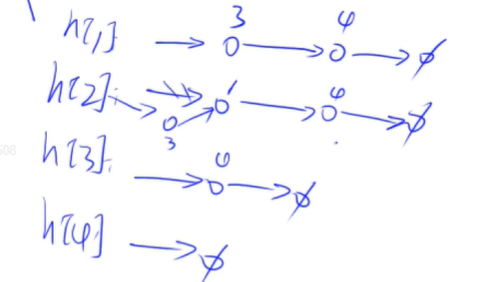
当想插入一条新的边时

先找到2这个点对应的单链表,然后把3插到里面去,一般用头插法
h[i]表示第i个点的头
树和图的遍历有两种方式,深度优先遍历和宽度优先遍历
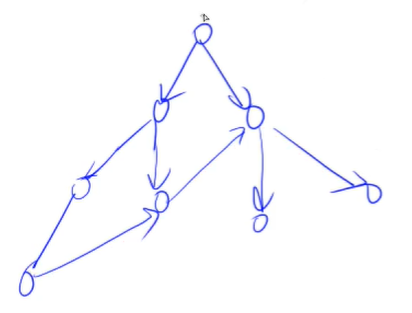
这个图的深度优先遍历是这样

宽度优先遍历是这样

注意一点,深度优先遍历和宽度优先遍历每一个点都只会遍历一次
树和图的深搜
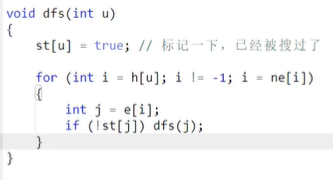
深度优先遍历可以算出来每一个子树中的点的数量
树和图的深度优先遍历和宽度优先遍历时间复杂度都是O(n + m)的,n是点,m是边
不一定非要从1开始搜,从哪个点开始都是一样的
1 #include <bits/stdc++.h> 2 using namespace std; 3 const int N = 100010, M = 2 * N; 4 int n; 5 int h[N], e[M], ne[M], idx; 6 //h[]数组存的是n个链表的链表头 7 //e[]数组存每一个节点的值是多少 8 //ne[]数组存每一个节点能next指针 9 bool st[N]; //存储哪些点已经遍历过了 10 int ans = N; 11 void add(int a, int b) { //插入一条a指向b的边 12 //在a对应的邻接表里插入一个节点b 13 e[idx] = b; 14 ne[idx] = h[a]; 15 h[a] = idx; 16 idx++; 17 } 18 //返回以u为根的子树的大小 19 int dfs(int u) { //u是当前已经遍历到的点 20 st[u] = true; //标记一下,当前这个点已经被搜过了 21 int sum = 1; //sum是当前这个子树的大小 22 int res = 0; //res是把这个点删除之后,剩下的每一个连通块的大小的最大值 23 for (int i = h[u]; i != -1; i = ne[i]) { //遍历一下u的所有出边 24 int j = e[i]; //当前这个链表里的节点对应于图中点的编号 25 if (!st[j]) { 26 int s = dfs(j); //s表示当前这个子树的大小 27 res = max(res, s); //当前这个子树也算是连通块 28 sum += s; //以这个儿子为根节点的子树是以u为根节点子树的一部分 29 } 30 } 31 //n - sum是上面连通块的数量 32 res = max(res, n - sum); 33 ans = min(ans, res); 34 return sum; 35 } 36 int main() { 37 cin >> n; 38 memset(h, -1, sizeof(h)); 39 for (int i = 0; i < n - 1; i++) { 40 int a, b; 41 cin >> a >> b; 42 add(a, b); 43 add(b, a); 44 } 45 dfs(1); //从第一个点开始搜 46 cout << ans << endl; 47 return 0; 48 }