9.筛法求欧拉函数

 按照线性筛法求质数的方法，用O(n)的时间，求出1 ~ n中每一个数的欧拉函数

在线性筛的过程中，顺便求欧拉函数

#include <bits/stdc++.h>
using namespace std;
const int N = 1e6 + 10;
typedef long long ll;
int primes[N], cnt;
bool st[N];
int phi[N]; //欧拉函数
ll get_eulers(int n) {
    phi[1] = 1;
    for (int i = 2; i <= n; i++) {
        if (!st[i]) {
            primes[cnt++] = i;
            //如果p这个数是质数的话，那么它的欧拉函数是p - 1
            phi[i] = i - 1;
        }
        for (int j = 0; primes[j] <= n / i; j++) {
            st[primes[j] * i] = true;
            if (i % primes[j] == 0) {
                //此时primes[j] * i这个数的欧拉函数是
                phi[primes[j] * i] = phi[i] * primes[j];
                break;
            }
            //pj一定是pj * i的最小质因子,而且pj还不包含在i的质因子当中
            phi[primes[j] * i] = phi[i] * (primes[j] - 1);
        }
    }
    ll res = 0;
    for (int i = 1; i <= n; i++) {
        res += phi[i];
    }
    return res;
}
int main() {
    int n;
    cin >> n;
    cout << get_eulers(n) << endl;
    return 0;
}

欧拉函数有什么用处

有一个欧拉定理：

 

 

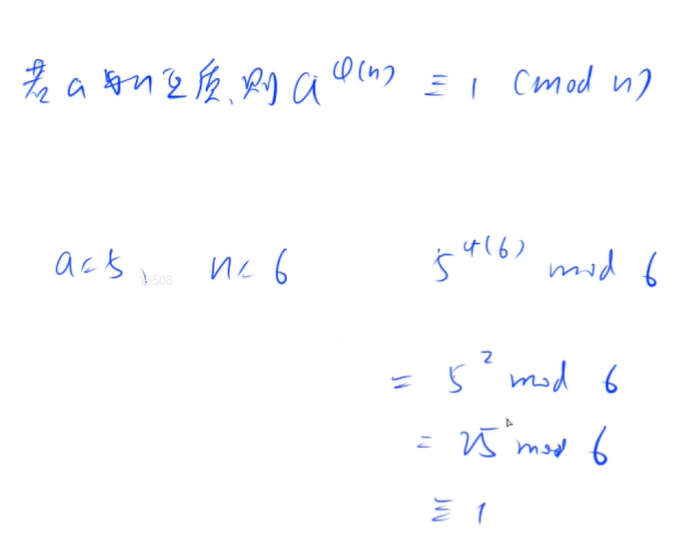
 欧拉定理有一个推论：当n是质数的时候，如果a和n互质，则有

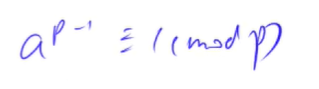
 这个就是费马小定理，也就是牛客暑期多校训练里卡了我们队三个小时的定理