中国剩余定理,又叫孙子定理

中国剩余定理是用来求解同余方程组的
给定一堆两两互质的数,m1, m2, ..., mk
用M表示所有mi的乘积
再定义Mi = 除了mi后,所有m的乘积。所以Mi和mi互质

这一步是用扩展欧几里德算法
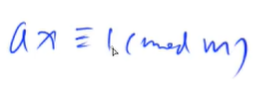
求逆等价于特殊的方程,右边不是b了,是1
由于m不一定是质数,所以用扩展欧几里德算法来求



先拿两个式子为例,分析一下



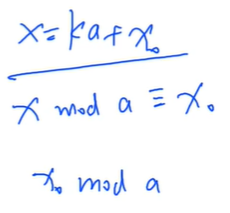
1 #include <bits/stdc++.h> 2 using namespace std; 3 typedef long long ll; 4 ll exgcd(ll a, ll b, ll &x, ll &y) { //扩展欧几里德算法模板 5 if (!b) { 6 x = 1; 7 y = 0; 8 return a; 9 } 10 ll d = exgcd(b, a % b, y, x); 11 y -= a / b * x; 12 return d; 13 } 14 int main() { 15 int n; 16 cin >> n; 17 bool has_answer = true; 18 ll a1, m1; //假设第一个方程是x mod a1 = m1 19 //要将两个式子合并成x = k * a1 + m1的形式 20 cin >> a1 >> m1; 21 for (int i = 0; i < n - 1; i++) { //然后把剩余方程合并入现有方程中 22 ll a2, m2; //假设新的方程是x mod a2 = m2 23 cin >> a2 >> m2; 24 //然后开始合并 25 //根据这个式子k1 * a1 - k2 * a2 = m2 - m1 (*) 26 ll k1, k2; //要求出来上式的系数 27 ll d = exgcd(a1, a2, k1, k2); //d = a1和a2的最大公约数 28 if ((m2 - m1) % d) { //若*式无解 29 has_answer = false; 30 break; 31 } 32 //能走到这说明有解 33 //上面用拓展欧几里德算法求出来的实际是 34 //k1 * a1 - k2 * a2 = d的系数 35 k1 *= (m2 - m1) / d; //等式两边同时乘以 36 ll t = a2 / d; //根据k1 + k * (a2 / d) 37 //只要求出一个k1,就能求出其通解 38 //k1 + k * (a2 / d) 39 k1 = (k1 % t + t) % t; //然后把k1变成最小的正整数解 40 //要将两个式子合并成x = k * a1 + m1的形式 41 m1 = a1 * k1 + m1; 42 a1 = abs(a1 / d * a2); //新式子的系数a1 43 44 } 45 if (has_answer) { 46 cout << (m1 % a1 + a1) % a1 << endl; 47 } else { 48 cout << -1 << endl; 49 } 50 return 0; 51 }