
高斯消元可以在O(n ^ 3)的时间复杂度内,求解一个包含n个方程和n个未知数的多元线性方程组

解有三种情况

预备知识:线性代数矩阵的初等行变换,转化成最短阶梯形矩阵
高斯消元就是把一个系数矩阵变换成上三角的形式
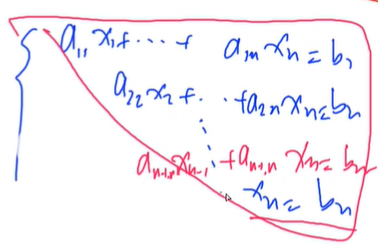
高斯消元涉及到的线代知识不多,秩之类的不涉及
只用最基础的线代知识
无解的情况:不完美阶梯形时,某一行出现了左边没有未知数,右边非零的情况。0 = ?这种情况,无解
无穷多解的情况:不完美阶梯形时,出现很多0 = 0的方程,无穷多组解
唯一解的情况:完美的上三角阶梯形矩阵,第一行n个未知数,第二行n - 1个,第n行1个未知数
 、
、
1 #include <bits/stdc++.h> 2 using namespace std; 3 const int N = 110; 4 const double eps = 1e-6; //判断是否是0 5 int n; 6 double a[N][N]; //用double存 7 int gauss() { 8 int c, r; 9 //c表示枚举的每一列 10 //r表示行 11 for (c = 0, r = 0; c < n; c++) { 12 int t = r; //t表示当前这一列绝对值最大的那一行 13 for (int i = r; i < n; i++) { //找到当前这一列,绝对值最大的那一行 14 if (fabs(a[i][c]) > fabs(a[t][c])) { 15 t = i; 16 } 17 } 18 if (fabs(a[t][c]) < eps) { //如果当前这一列是0了 19 continue; 20 } 21 for (int i = c; i <= n; i++) { //换到最上面 22 swap(a[t][i], a[r][i]); 23 } 24 for (int i = n; i >= c; i--) { //变成1,倒着来 25 a[r][i] /= a[r][c]; 26 } 27 for (int i = r + 1; i < n; i++) { //把下面的都变为0 28 if (fabs(a[i][c]) > eps) { //已经是0就不操作 29 for (int j = n; j >= c; j--) { 30 a[i][j] -= a[r][j] * a[i][c]; 31 } 32 } 33 } 34 r++; 35 } 36 //已经变好了 37 if (r < n) { //如果不到n个方程,不是唯一解 38 for (int i = r; i < n; i++) { 39 if (fabs(a[i][n]) > eps) { //如果出现了0 = ?的情况 40 return 2; //无解 41 } 42 } 43 return 1; //无穷多解 44 } 45 for (int i = n - 1; i >= 0; i--) { //最后一步,倒着把答案推出来 46 for (int j = i + 1; j < n; j++) { 47 a[i][n] -= a[j][n] * a[i][j]; 48 } 49 } 50 return 0; //唯一解 51 } 52 int main() { 53 cin >> n; 54 for (int i = 0; i < n; i++) { 55 for (int j = 0; j < n + 1; j++) { 56 cin >> a[i][j]; 57 } 58 } 59 int t = gauss(); 60 if (t == 0) { //唯一解 61 for (int i = 0; i < n; i++) { 62 cout << fixed << setprecision(2) << a[i][n] << endl; 63 } 64 } else if (t == 1) { //无穷多解 65 cout << "Infinite group solutions" << endl; 66 } else { //无解 67 cout << "No solution" << endl; 68 } 69 return 0; 70 }