16.高斯消元解异或线性方程组

 

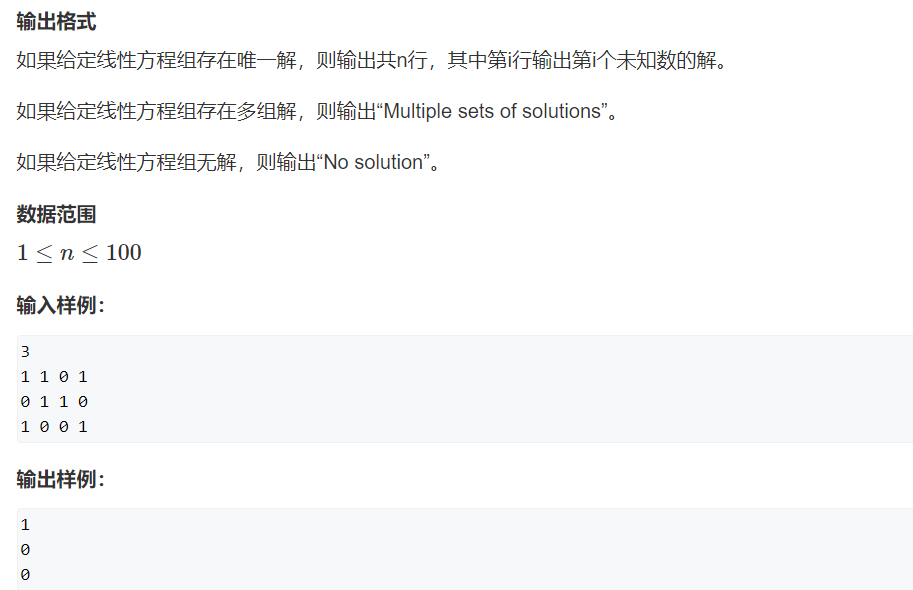
 样例解释：

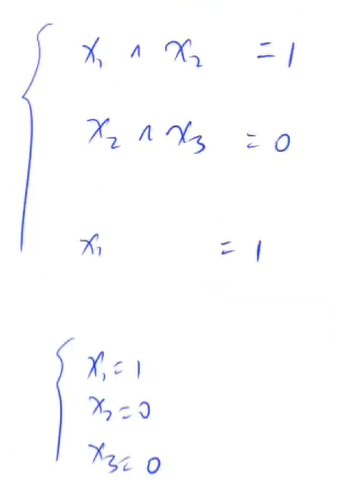
 异或又叫不进位加法

思路：

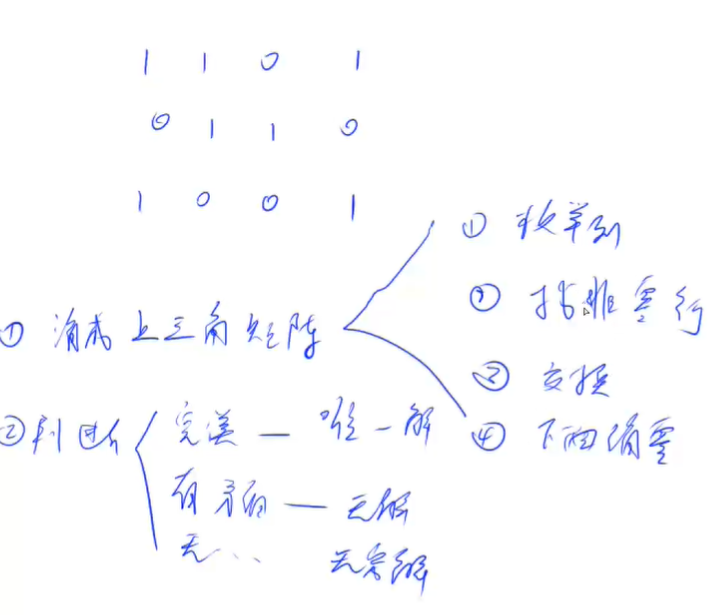
 原题样例转换为上三角矩阵后是这样

 有唯一解

求出唯一解后，反推一遍，就可以求出所有解

异或版的高斯消元，比普通版的高斯消元更容易。为数不多的衍生题比母题简单系列

#include <bits/stdc++.h>
using namespace std;
const int N = 110;
int n;
int a[N][N];
int gauss() {
    int c, r;
    //c表示枚举的每一列
    //r表示行
    for (c = 0, r = 0; c < n; c++) {
        int t = r;
        for (int i = r; i < n; i++) { 
            if (a[i][c]) {
                t = i;
                break;
            }
        }
        if (!a[t][c]) { 
            continue;
        }
        for (int i = c; i <= n; i++) { //换到最上面
            swap(a[t][i], a[r][i]);
        }
        for (int i = r + 1; i < n; i++) { //把下面的都变为0
            if (a[i][c]) { 
                for (int j = n; j >= c; j--) {
                    a[i][j] ^= a[r][j];
                }
            }
        }
        r++;
    }
    //已经变好了
    if (r < n) { //如果不到n个方程，不是唯一解
        for (int i = r; i < n; i++) {
            if (a[i][n]) { //如果出现了0 = ?的情况
                return 2; //无解
            }
        }
        return 1; //无穷多解
    }
    for (int i = n - 1; i >= 0; i--) { //最后一步，倒着把答案推出来
        for (int j = i + 1; j < n; j++) {
            a[i][n] ^= a[i][j] * a[j][n]; //*可以写成&
        }
    }
    return 0; //唯一解
}
int main() {
    cin >> n;
    for (int i = 0; i < n; i++) {
        for (int j = 0; j < n + 1; j++) {
            cin >> a[i][j];
        }
    }
    int t = gauss();
    if (t == 0) { //唯一解
        for (int i = 0; i < n; i++) {
            cout << a[i][n] << endl;
        }
    } else if (t == 1) { //无穷多解
        cout << "Multiple sets of solutions" << endl;
    } else { //无解
        cout << "No solution" << endl;
    }
    return 0;
}