18.求组合数 II

 

上一题是直接预处理出来了这个值是多少，这道题是预处理求值过程中间的一步

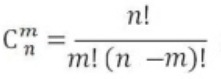
 根据这个公式，预处理出来fact[i] = i! % mod的结果

然后再用逆元运算，把除法变成乘法

再预处理一个infact[i] 

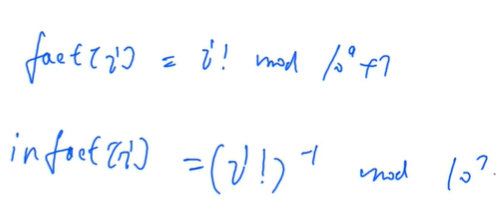
 预处理完之后，就可以计算了

 因为除以一个数对m取模等于乘以这个数的逆元对m取模

求逆元可以用快速幂，因为1e9 + 7是个质数，可以用费马小定理

#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
const int N = 100010, mod = 1e9 + 7;
ll fact[N], infact[N]; //存储的都是模上mod的值
ll qmi(ll a, ll k, ll p) {
    ll res = 1;
    while (k) {
        if (k & 1) {
            res = res * a % p;
        }
        a = a * a % p;
        k >>= 1;
    }
    return res;
}
int main() {
    fact[0] = infact[0] = 1; //边界情况，0! = 1
    for (int i = 1; i < N; i++) {
        fact[i] = fact[i - 1] * i % mod;
        infact[i] = infact[i - 1] * qmi(i, mod - 2, mod) % mod;
    }
    int n;
    cin >> n;
    while (n--) {
        int a, b;
        cin >> a >> b;
        cout << fact[a] * infact[a - b] % mod * infact[b] % mod << endl;
    }
    return 0;
}