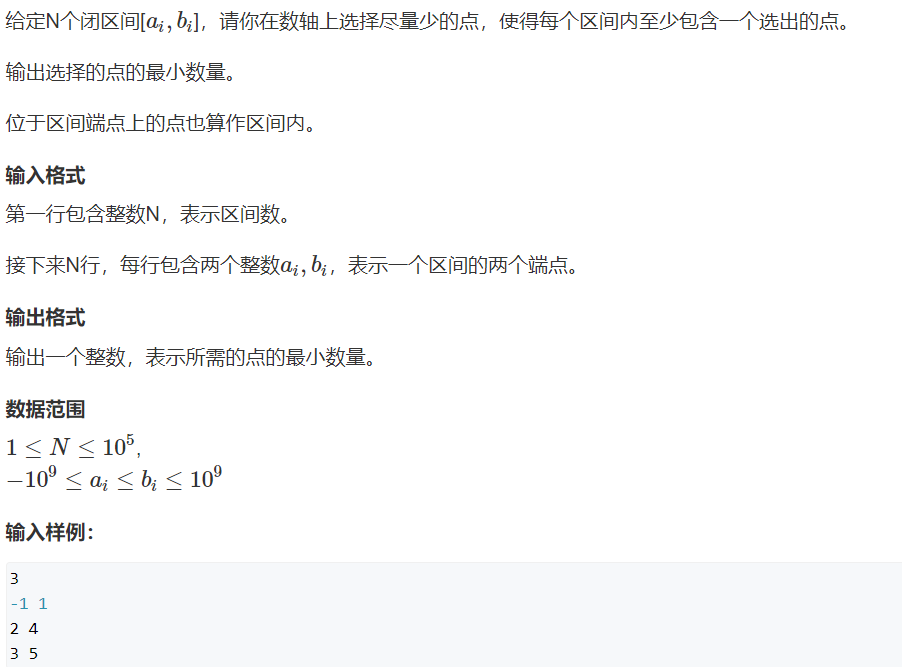

区间问题一般都需要对区间进行排序,对左端点排序,或对右端点排序,或双关键字排序
然后需要证明这样的选法选出来的点数一定是符合答案的,且是选点最少的
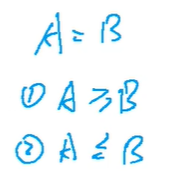
首先按照这个方法来选的话,每一个区间上一定选了一个点,所以这种选法是一种合法的方案
然后这道题的最优解是指所有合法方案中的选点最少的,所以

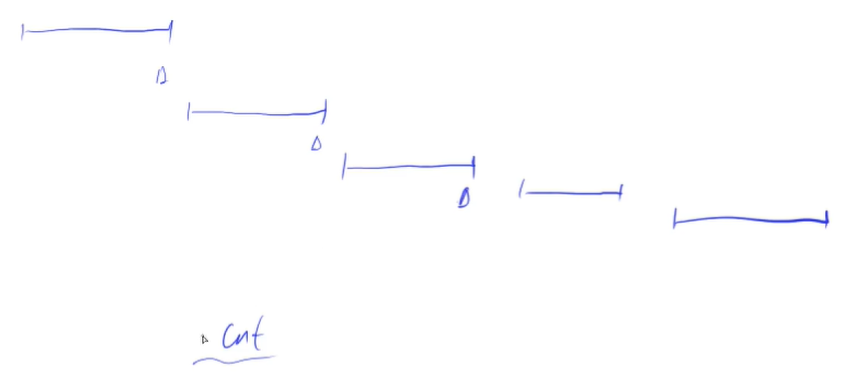

所以ans = cnt
1 #include <bits/stdc++.h> 2 using namespace std; 3 const int N = 100010; 4 struct Range { 5 int l, r; 6 } range[N]; 7 bool cmp(Range r1, Range r2) { 8 return r1.r < r2.r; 9 } 10 int main() { 11 int n; 12 cin >> n; 13 for (int i = 0; i < n; i++) { 14 int l, r; 15 cin >> l >> r; 16 range[i] = {l, r}; 17 } 18 sort(range, range + n, cmp); 19 int res = 0, ed = -2e9; 20 //ed表示上一个点的下标 21 for (int i = 0; i < n; i++) { 22 if (range[i].l > ed) { 23 res++; 24 ed = range[i].r; 25 } 26 } 27 cout << res << endl; 28 return 0; 29 }