题意
题目给出一个字符串,可能有P、A、T或其他字符。现在需要根据以下几个条件来判断该字符串能否输出“YES”。
条件1:如果出现P、A、T以外的字符,输出“NO”;初始状态下P和T必须各恰好有一个,且P在T左边,P和T之间至少有一个A,否则输出“NO”。
条件2:PAT、APATA、AAPATAA、AAAPATAAA、... 、xPATx都输出“YES",这里x为空或是任意数量的A。
条件3:假设有一个字符串的格式是aPbTc,这里a、b、c可以为空或是任意数量的A,例如PAT、APAAT、AAAPTA都满足这个格式。如果这个字符串aPbTc已知是YES,那么在b与T之间添加一个A、c后面添加字符串a之后形成的新字符串aPbATca也是YES。例如PAT是YES,那么PAAT也是YES;PAAT是YES,那么PAAAT也是YES;APATA是YES(因为满足条件2),那么APAATAA也是YES。
现在让你通过这三个条件来判断输入的字符串是否应该输出“YES”。
思路
思考这三个条件,可以注意到:条件2给出的字符串是最底层YES的,且条件2的P与T中间有且只有一个A,而由条件3得到的所有字符串一开始一 定是条件2中的字符串变形而来。
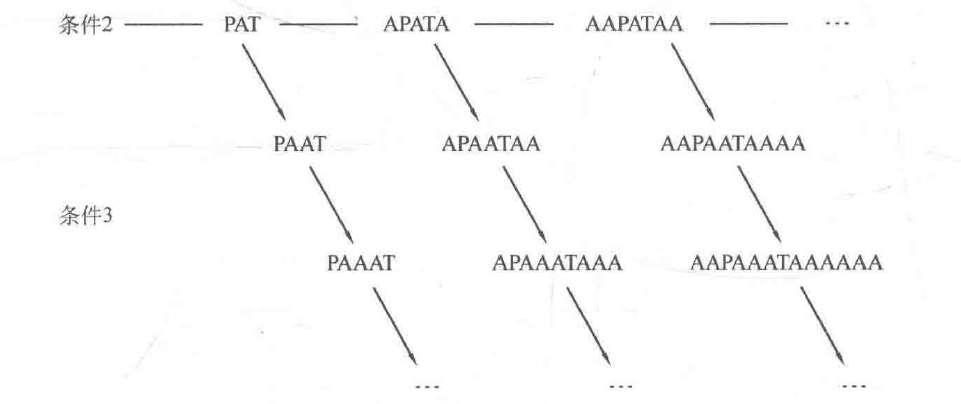
如图所示,所有YES最开始都源于条件2,条件3是在条件2的基础上进行的扩充。对每一个满足条件2的字符串,都可以由条件3一个接一个生成新的字符串,并且这也是生成新的YES字符串的唯一方法, 即在PT中间加一个A,在字符串后面加上P前面的所有A。
由此可以得到灵感:对给出的字符串,先判断其是否通过条件1的检验。之后,记录P左边A的个数为x、P和T中间A的个数为y. T右边A的个数为z。考虑到条件3得到新字符串的过程是在PT中间加一个A、字符串后面加上P前面的所有A,因此可以知道,每使用条件3一次,x不变、y变为y+ 1、z变为z+x。反过来,如果沿着箭头逆回去,每逆一次,x不变、y变为y-1、z变为z-x。这样可以一直逆回去,直到y==1时(即P和T中间只有一个A时)判断x和z是否相等:如果x=z。则输出“YES";否则,输出“NO”。
总的来说,就是对初始字符串通过条件3的逆运算不断回退,直到可以判断条件2是否成立。
讲到这里,这题已经很好做了。但是如果进一步分析可以发现一些规律,从而更快解出答案:
这里x、y、z的含义和上面一样,由于y每次回退的步骤中都减1,因此从初始字符串回退到PT之间只剩一个A,需要进行y-1次回退。而T右边A的个数z在经过y-1次回退后(z每次减x)将变为z-x * (y-1)。这时,判断条件2成立的条件是z-x * (y-1)是否等于P左边A的个数x(因为条件2中P左边和T右边的A的个数是相等的,且在回退的过程中x不发生变化):如果z-x * (y-1) == x,则输出“YES";否则,输出“NO”。
所以一句话总结字符串的要求:只能有一个P一个T,中间末尾和开头可以随便插入A。但是必须满足开头的A的个数 * 中间的A的个数 = 结尾的A的个数,而且P和T中间不能没有A。
bool check(string s)
{
int cntp=0,cnta=0,cntt=0,other=0;
int posp=0,post=0;
for(int i=0;i<s.size();i++)
if(s[i] == 'P')
{
cntp++;
posp=i;
}
else if(s[i] == 'A') cnta++;
else if(s[i] == 'T')
{
cntt++;
post=i;
}
else other++;
if(cntp != 1 || cntt != 1 || other || post-posp <= 1)
return false;
int x=posp,y=post-posp-1,z=s.size()-1-post;
if(z != x*y)
return false;
return true;
}
int main()
{
int T;
cin>>T;
while(T--)
{
string s;
cin>>s;
if(check(s)) puts("YES");
else puts("NO");
}
//system("pause");
return 0;
}