在前面一篇blog中 (http://www.cnblogs.com/fxjwind/archive/2011/07/05/2098642.html), 我记录了相关的海量文档查同问题, 这儿就系统的来记录一下对于大规模数据挖掘技术而言, 怎样finding similar items……
1 Applications of Near-Neighbor Search
The Jaccard similarity of sets S and T is |S ∩ T |/|S ∪ T |, that is, the ratio of the size of the intersection of S and T to the size of their union. We shall denote the Jaccard similarity of S and T by SIM(S, T ).
Similarity of Documents, finding textually similar documents in a large corpus such as the Web or a collection of news articles.
Collaborative filtering, a process whereby we recommend to users items that were liked by other users who have exhibited similar tastes.
On-Line Purchases, Amazon.com has millions of customers and sells millions of items. Its database records which items have been bought by which customers. We can say two customers are similar if their sets of purchased items have a high Jaccard similarity.
2 Shingling of Documents
2.1 k-Shingles
A document is a string of characters. Define a k-shingle for a document to be any substring of length k found within the document.
Example 3.3 : Suppose our document D is the string abcdabd, and we pick k = 2. Then the set of 2-shingles for D is {ab, bc, cd, da, bd}.
2.2 Choosing the Shingle Size
Thus, if our corpus of documents is emails, picking k = 5 should be fine.
275=14,348,907 possible shingles. Since the typical email is much smaller than 14 million characters long, we would expect k = 5 to work well, and indeed it does.
For large documents, such as research articles, choice k = 9 is considered safe.
2.3 Hashing Shingles
Instead of using substrings directly as shingles, we can pick a hash function that maps strings of length k to some number of buckets and treat the resulting bucket number as the shingle. The set representing a document is then the
Not only has the data been compacted, but we can now manipulate (hashed) shingles by single-word machine operations.
2.4 Shingles Built from Words
An alternative form of shingle has proved effective for the problem of identifying similar news articles.
News articles, and most prose, have a lot of stop words, the most common words such as “and,” “you,” “to,” and so on.
Defining a shingle to be a stop word followed by the next two words, regardless of whether or not they were stop words, formed a useful set of shingles.
Example 3.5 : An ad might have the simple text “Buy Sudzo.” However, a news article with the same idea might read something like “A spokesperson for the Sudzo Corporation revealed today that studies have shown it is good for people to buy Sudzo products.”
The first three shingles made from a stop word and the next two following are:
A spokesperson for
for the Sudzo
the Sudzo Corporation
3 Similarity-Preserving Summaries of Sets
Sets of shingles are large. Even if we hash them to four bytes each, the space needed to store a set is still roughly four times the space taken by the document. If we have millions of documents, it may well not be possible to store all the shingle-sets in main memory.
Our goal in this section is to replace large sets by much smaller representations called “signatures.”
3.1 Matrix Representation of Sets

Example 3.6 : An example of a matrix representing sets chosen from the universal set {a, b, c, d, e}. Here, S1 = {a, d}, S2 = {c}, S3 = {b, d, e}, and S4 = {a, c, d}.
这儿可以直接将每一列作为该集合的signature, 不过由于element往往会非常多, 所以会导致signature太长, 下面就介绍用minhashing来压缩signature.
3.2 Minhashing

Example 3.7 : Let us suppose we pick the order of rows ‘beadc’ for the matrix of Example 3.6. This permutation defines a minhash function h that maps sets to rows. In this matrix, we can read off the values of h by scanning from the top until we come to a 1. Thus, we see that h(S1) = a, h(S2) = c, h(S3) = b, and h(S4) = a.
3.3 Minhashing and Jaccard Similarity
The probability that the minhash function for a random permutation of rows produces the same value for two sets equals the Jaccard similarity of those sets.
对于一个随机的行排列(permutation), 两个集合minhash得到的相同值的概率就是他们的Jaccard similarity.
如上图的S1和S4, minhash值都为a, 就是这两个集合都包含a, 这个概率就应该和Jaccard similarity相同.
这保证了使用Minhashing的正确性, Jaccard similarity作为判断两个sets是否相似的基本原理, 越高说明两个集合越相似
通过这个定理, 转化为当两个集合的minhashing越相似, 则说明两个集合越相似
3.4 Minhash Signatures
Perhaps 100 permutations or several hundred permutations will do. Call the minhash functions determined by these permutations h1, h2, . . . , hn. From the column representing set S, construct the minhash signature for S, the vector [h1(S), h2(S), . . . , hn(S)].
对于一种排列可以算出一个minhash值, 对于n中随机排列, 就可以算出n个minhash值, 把这n个值组合作为集合的签名. 原理就是特征抽样, 从而达到签名大小的大大压缩. 这儿签名大小是由选取的permutations 个数决定的.
3.5 Computing Minhash Signatures
It is not feasible to permute a large characteristicmatrix explicitly. Even picking a random permutation of millions or billions of rows is time-consuming, and the necessary sorting of the rows would take even more time.
实际去permuate矩阵是低效的, 我们就去模拟这种permuate, 思路也很简单,
a random hash function that maps row numbers to as many buckets as there are rows.
Thus, instead of picking n random permutations of rows, we pick n randomly chosen hash functions h1, h2, . . . , hn on the rows.
用random hash函数来随机化行号的排列来模拟矩阵的随机化排列.
4 Locality-Sensitive Hashing for Documents
Even though we can use minhashing to compress large documents into small signatures, it still may be impossible to find the pairs with greatest similarity efficiently. The reason is that the number of pairs of documents may be too large, even if there are not too many documents.
虽然通过minhashing可以将大文本压缩成较小的signature, 从而大大优化了文档两两比较的速度, 但是再快也抗不住多, 如果要在billion级别的文档集合里面找出duplicated文档, 还需要其他的技术.
If our goal is to compute the similarity of every pair, there is nothing we can do to reduce the work, although parallelism can reduce the elapsed time. However, often we want only the most similar pairs or all pairs that are above some lower bound in similarity. If so, then we need to focus our attention only on pairs that are likely to be similar, without investigating every pair. There is a general theory of how to provide such focus, called locality-sensitive hashing (LSH) or near-neighbor search.
基本的思路还是, 不能每个都比, 那样肯定很慢, 必须先进行筛选, 只比较那些有可能duplicated或similiar的
4.1 LSH for Minhash Signatures
One general approach to LSH is to “hash” items several times, in such a way that similar items are more likely to be hashed to the same bucket than dissimilar items are. We then consider any pair that hashed to the same bucket for any of the hashings to be a candidate pair. We check only the candidate pairs for similarity.
我们应该尽量避免不同的items被hash到同一个bucket, 而被误认为成candidate (false positives), 尽量保证相同的items至少一次被hash到同一个bucket, 从而避免candidat被漏掉 (false negatives)
个人认为, 对于一般的任务, 应该在保证一定的false positives的同时, 尽量减少false negatives, 因为发生false negatives是无法弥补的.
If we have minhash signatures for the items, an effective way to choose the hashings is to divide the signature matrix into b bands consisting of r rows each.
上面说的方法是hash多次, 这儿的方法是, 如果对于每个文档都已经有n位的minhash signatures, 可以将其分成b段, 每段r位(b*r = n).
For each band, there is a hash function that takes vectors of r integers (the portion of one column within that band) and hashes them to some large number of buckets.
将每个文档的第i段(1<i<b), 单独进行hash. 只有在任一段上, 两个文档的hash值相同, 就认为这两个文档有相同的可能.
The more similar two columns are, the more likely it is that they will be identical in some band. Thus, intuitively the banding strategy
makes similar columns much more likely to be candidate pairs than dissimilar pairs.
4.2 Analysis of the Banding Technique
Suppose we use b bands of r rows each, and suppose that a particular pair of documents have Jaccard similarity s.
根据前面的定理,
the probability the minhash signatures for these documents agree in any one particular row of the signature matrix is s.
那么, 一段中r位都相同的概率为, sr
一段中r位至少有一位不同的概率, 1-sr
b段中r位都至少有一位不同的概率, (1 - sr)b
所以, b段中有至少一段完全相同的概率为, 1- (1 - sr)b
Example 3.11 : b = 20 and r = 5, s = 0.8, 则 1- (1 - sr)b = 0.99965
可以证明, 这个分段技术是可行的.
4.3 Combining the Techniques
We can now give an approach to finding the set of candidate pairs for similar documents and then discovering the truly similar documents among them.
1. Pick a value of k and construct from each document the set of k-shingles. Optionally, hash the k-shingles to shorter bucket numbers.
2. Sort the document-shingle pairs to order them by shingle.
3. Pick a length n for the minhash signatures. Feed the sorted list to the algorithm of Section 3.3.5 to compute the minhash signatures for all the documents.
4. Choose a threshold t that defines how similar documents have to be in order for them to be regarded as a desired “similar pair.” Pick a number of bands b and a number of rows r such that br = n, and the threshold t is approximately (1/b)1/r. If avoidance of false negatives is important, you may wish to select b and r to produce a threshold lower than t; if speed is important and you wish to limit false positives, select b and r to produce a higher threshold.
5. Construct candidate pairs by applying the LSH technique of Section 3.4.1.6. Examine each candidate pair’s signatures and determine whether the fraction of components in which they agree is at least t.
7. Optionally, if the signatures are sufficiently similar, go to the documents themselves and check that they are truly similar, rather than documents that, by luck, had similar signatures.
这其中解决了两个问题, 文档本身不利于相互比较和在海量文档中怎样挑选需要比较的candidate
1~3步解决了第一个问题, 把文档->shingles->shingles hash –> minhash signature, 这是个逐渐压缩的过程, 到最后变成minhash signature时, 已经很适合相互比较了, 并且重要的是minhash signature的相似形可以直接反映出文档间的相似度(Jaccard similarity).
4~7步解决了第二个问题, 通过LSH来筛选需要比较的candidate, 从而达到对海量文档的高效比较.
5 Distance Measures
We now take a short detour to study the general notion of distance measures.
5.1 Definition of a Distance Measure
A distance measure on this space is a function d(x, y) that takes two points in the space as arguments and produces a real number, and satisfies the following axioms:
1. d(x,y) >= 0
2. d(x,y) == 0 当且仅当x=y
3. d(x,y) == d(y,x)
4. d(x,y) <= d(x,z) + d(z,y)
5.2 Euclidean Distances
The most familiar distance measure is the one we normally think of as “distance.” 两点间的绝对距离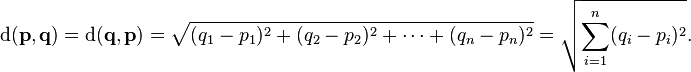
5.3 Jaccard Distance
Jaccard distance of sets by d(x, y) = 1 − SIM(x, y). That is, the Jaccard distance is 1 minus the ratio of the sizes of the intersection and union of sets x and y.
用来表示两个集合间的相似度.
5.4 Cosine Distance
The cosine distance between two points is the angle that the vectors to those points make. This angle will be in the range 0 to 180 degrees.
The dot product can be defined for two vectors ![]() and
and ![]() by
by ![]() So
So
不同于欧氏距离, 计算的不是两点间绝对距离, 是两点向量间的夹角的大小. 所以和欧氏距离适用于不同的场景, 在实际中更为常用.
5.5 Edit Distance
This distance makes sense when points are strings. The distance between two strings x = x1x2 · · · xn and y = y1y2 · · · ym is the smallest number of insertions and deletions of single characters that will convert x to y.
Example 3.14 : The edit distance between the strings x = abcde and y = acfdeg is 3. To convert x to y:
1. Delete b.
2. Insert f after c.
3. Insert g after e.
The way to calculate the edit distance d(x, y) is to compute a longest common subsequence (LCS) of x and y.
The edit distance d(x, y) can be calculated as the length of x plus the length of y minus twice the length of their LCS.
LCS(最长公共子序列)通过动态规划来实现, 参见(http://www.cnblogs.com/fxjwind/archive/2011/07/04/2097752.html)
Example 3.15 : The strings x = abcde and y = acfdeg from Example 3.14 have a unique LCS, which is acde.
The edit distance is thus 5 + 6 − 2 × 4 = 3
5.6 Hamming Distance
Given a space of vectors, we define the Hamming distance between two vectors to be the number of components in which they differ.
Example 3.16 : The Hamming distance between the vectors 10101 and 11110 is 3.
6 The Theory of Locality-Sensitive Functions
We shall explore other families of functions, besides the minhash functions, that can serve to produce candidate pairs efficiently.
Our first step is to define “locality-sensitive functions” generally.
6.1 Locality-Sensitive Functions
We shall consider functions that take two items and render a decision about whether these items should be a candidate pair.
A collection of functions of this form will be called a family of functions.
Let d1 < d2 be two distances according to some distance measure d. A family F of functions is said to be (d1, d2, p1, p2)-sensitive if for every f in F:
1. If d(x, y) ≤ d1, then the probability that f(x) = f(y) is at least p1.
2. If d(x, y) ≥ d2, then the probability that f(x) = f(y) is at most p2.
一组函数族(families of functions), 对于族内的任一函数,
当两点距离相近时, d(x, y) ≤ d1, 那么这个两点的由该函数产生的hash值相等的概率至少是p1
当两点距离比较远时, d(x, y) ≥ d2, 那么这个两点的由该函数产生的hash值相等的概率最多是p2
简单的说就是, 越相近, 产生的hash值相等的概率就越大, 这样这个函数族F就是Locality-Sensitive Functions, 并且是(d1, d2, p1, p2)-sensitive
6.2 Locality-Sensitive Families for Jaccard Distance
下面根据上面general的locality-sensitive functions的定义, 先来定义一下基于Jaccard Distance的Locality-Sensitive Families , minhash functions,
Use the family of minhash functions, and assume that the distance measure is the Jaccard distance.
The family of minhash functions is a (d1, d2, 1−d1, 1−d2)-sensitive family for any d1 and d2, where 0 ≤ d1 < d2 ≤ 1.
由下面这个定理,不难证明这个定义,
Jaccard similarity of x and y is equal to the probability that a minhash function will hash x and y to the same value.
6.3 Amplifying a Locality-Sensitive Family
怎样扩展Locality-Sensitive Family?
Suppose we are given a (d1, d2, p1, p2)-sensitive family F. can we construct a new family F′?
方法就是用先有family F中的r个functions来组合成新的function
Each member of F′ consists of r members of F for some fixed r. If f is in F′, and f is constructed from the set {f1, f2, . . . , fr} of members of F, we say f(x) = f(y) if and only if fi(x) = fi(y) for all i = 1, 2, . . . , r.
组合的方式有两种, And, OR, 所得到的famliy也是不同的
AND-construction
F′ is a (d1, d2, (p1)r, (p2)r)-sensitive family
OR-construction
F′ is a (d1, d2, 1 − (1 − p1)b, 1 − (1 − p2)b) -sensitive family
AND-construction lowers all probabilities, but if we choose F and r judiciously, we can make the small probability p2 get very close to 0, while the higher probability p1 stays significantly away from 0.
OR-construction makes all probabilities rise, but by choosing F and b judiciously, we can make the larger probability p1 approach 1 while the smaller probability p2 remains bounded away from 1.
We can cascade AND- and OR-constructions in any order to make the low probability close to 0 and the high probability close
to 1. 这儿需要一个balance来达到比较合理的false positives and false negatives.
这个牛了, 通过一个Locality-Sensitive Family, 可以扩展出无数的Locality-Sensitive Family, 并通过不同的And, Or组合达到更好的效果.
7 LSH Families for Other Distance Measures
除了Jaccard Distance, 下面会介绍基于其他距离的LSH Families
7.1 LSH Families for Hamming Distance
Suppose we have a space of d-dimensional vectors, and h(x, y) denotes the Hamming distance between vectors x and y. If we take any one position of the vectors, say the ith position, we can define the function fi(x) to be the ith bit of vector x. Then fi(x) = fi(y) if and only if vectors x and y agree in the ith position.
Then the probability that fi(x) = fi(y) for a randomly chosen i is exactly 1 − h(x, y)/d.
如果理解Hamming距离的话, 这个不难理解, 只有h(x, y)位需要改, 排除了这h(x, y)位, 其他位都是相等的.
The family F consisting of the functions {f1, f2, . . . , fd} is a (d1, d2, 1 − d1/d, 1 − d2/d)-sensitive family of hash functions, for any d1 < d2.
这儿给出了定义但没有给出具体什么样的functions famliy可以满足这样的条件.
而对于Jaccard Distance, 给出了具体的functions famliy, MinHash.
7.2 Random Hyperplanes and the Cosine Distance
Each hash function f in our locality-sensitive family F is built from a randomly chosen vector vf . Given two vectors x and y, say f(x) = f(y) if and only if the dot products vf .x and vf .y have the same sign. Then F is a locality-sensitive family for the cosine distance.
That is, F is a (d1, d2, (180 − d1)/180, d2/180)-sensitive family of hash functions.
前面文章介绍的Charikar's simhash就应该是一种Cosine Distance的LSH Families .
7.4 LSH Families for Euclidean Distance
也是基于一种投影的方式...不详细说了