Machine Learning in Action – PCA和SVD

降维技术，
首先举的例子觉得很好，因为不知不觉中天天都在做着降维的工作

对于显示器显示一个图片是通过像素点0，1，比如对于分辨率1024×768的显示器，就需要1024×768个像素点的0，1来表示，这里每个像素点都是一维，即是个1024×768维的数据。而其实眼睛真正看到的只是一副二维的图片，这里眼睛其实在不知不觉中做了降维的工作，把1024×768维的数据降到2维

降维的好处，显而易见，数据更易于显示和使用，去噪音，减少计算量，更容易理解数据
主流的降维技术，包含：
主成分分析，principal component analysis(PCA)
因子分析，factor analysis
独立成分分析，independent component nalysis (ICA)

这些技术参考NG的课程笔记，这里给出PCA的python实现

PCA的实现很简单，求协方差矩阵的特征值和特征向量，并取特征值top的那些特征向量作为新的坐标轴（原因参考NG讲义）

from numpy import *
def loadDataSet(fileName, delim='	'):
    fr = open(fileName)
    stringArr = [line.strip().split(delim) for line in fr.readlines()]
    datArr = [map(float,line) for line in stringArr]
    return mat(datArr)
def pca(dataMat, topNfeat=9999999):
    meanVals = mean(dataMat, axis=0)
    meanRemoved = dataMat - meanVals  #Normalization
    covMat = cov(meanRemoved, rowvar=0) #生成协方差矩阵
    eigVals,eigVects = linalg.eig(mat(covMat)) #求解协方差矩阵的特征值，特征向量
    eigValInd = argsort(eigVals)
    eigValInd = eigValInd[:-(topNfeat+1):-1] #选取top特征值
    redEigVects = eigVects[:,eigValInd] #找到对应的特征向量
    lowDDataMat = meanRemoved * redEigVects #用特征向量生成新的数据
    reconMat = (lowDDataMat * redEigVects.T) + meanVals #为了调试恢复原始数据
    return lowDDataMat, reconMat

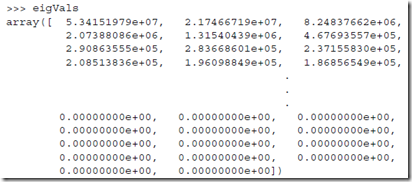
至于topNfeat取值，即选取多少个top的特征值，其实看到实际数据就可以决定，因为往往从某个特征值开始会和前面的相差几个数量级

比如底下的例子，

 

参考NG的讲义，对于高维的数据，算出协方差矩阵本身就是很耗的，所以其实可以用SVD分解来进行PCA，当然这个只是SVD的一个用法

但是理解singular value decomposition (SVD)还是看看SVD最经典的应用latent semantic indexing (LSI)
文档是由词组成，所以在比较文章的相似性时，比如分类或聚类时，会以词作为特征
这样的问题是，无法处理同义词，比如learn和study，或拼错的词

而如果此时对于m篇文章，n个词的矩阵做奇异值分解，就可以自动将词和文章进行分类

并将维数从词数降到分类树，即从n降到r

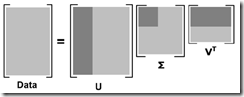
听上去很神奇，其实原理和PCA是一样的，因为SVD分解后
U是 的特征向量(eigenvector)矩阵，而 是词之间的协方差矩阵
并且U是m×r而不是m×n，已经进行了降维，U是取top r的特征向量，和PCA的过程是一样的
所以看上去是给词做了分类，其实只是将坐标轴旋转到特征向量，并取top进行降维

同理V是DataT*Data的特征向量矩阵，而DataT*Data是文本之间的协方差矩阵

所有SVD分解后，得到

U，每行表示该文本和每个词类的关系
V，每行表示该词和每个文本类的关系
奇异矩阵，表示词类和文本类之间的关系

个人理解，SVD其实是在自变量x和因变量y上同时进行了PCA降维
而普通PCA只是会降低x的维度
比如上面的例子，同时对于词和文章，进行特征向量的旋转和降维，得到词类和文章类

现在SVD分解更多的用在推荐系统，推荐系统最经典的就是协同过滤(Collaborative filtering)，item-base或user-base
用SVD可以达到更有效的推荐的效果
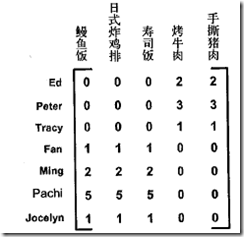
比如底下是用户对各个菜评分表，0表示没吃过

如果对这个做SVD分解，会得到两个奇异值
你会发现可以分别对应到美食BBQ和日式食品两类食品上
同时得到的结论，一拨人喜欢美食BBQ， 一拨人喜欢日式食品，这样推荐就很简单

python中实现svd很简单，有现成的函数，

输入，

def loadExData():
    return[[1, 1, 1, 0, 0],
        [2, 2, 2, 0, 0],
        [1, 1, 1, 0, 0],
        [5, 5, 5, 0, 0],
        [1, 1, 0, 2, 2],
        [0, 0, 0, 3, 3],
        [0, 0, 0, 1, 1]]

SVD分解，

>>> import svdRec
>>> Data=svdRec.loadExData()
>>> U,Sigma,VT=linalg.svd(Data)
>>> Sigma
array([ 9.72140007e+00, 5.29397912e+00, 6.84226362e-01,
7.16251492e-16, 4.85169600e-32])

可以看到奇异值中，最后两个的量级很小，可以忽略，所以取前3个值

所以r=3，做下面的近似

重新构造一个3×3的奇异矩阵，

>>> Sig3=mat([[Sigma[0], 0, 0],[0, Sigma[1], 0], [0, 0, Sigma[2]]])

截取特征值，产生新的数据，这步只是为了验证确实是能得到近似结果

>>> U[:,:3]*Sig3*VT[:3,:]
    array([[ 1., 1., 1., 0., 0.],
        [ 2., 2., 2., -0., -0.],
        [ 1., 1., 1., -0., -0.],
        [ 5., 5., 5., 0., 0.],
        [ 1., 1., -0., 2., 2.],
        [ 0., 0., -0., 3., 3.],
        [ 0., 0., -0., 1., 1.]])

 

下面实际看个推荐的例子，

经典的item-based的协同过滤，

#计算user和item之间的相似度
#simMeas，给出相似度计算方法，比如欧几里德距离，pearson相关系数，余弦法
def standEst(dataMat, user, simMeas, item):
    n = shape(dataMat)[1]
    simTotal = 0.0; ratSimTotal = 0.0
    for j in range(n): #遍历所有的item
        userRating = dataMat[user,j]
        if userRating == 0: continue #如果这个item，user没有评过，没有相关性
        #找出item和j都有评论的user的index
        overLap = nonzero(logical_and(dataMat[:,item].A>0, dataMat[:,j].A>0))[0]
        if len(overLap) == 0: similarity = 0 #没有交集没有相关性
        else: similarity = simMeas(dataMat[overLap,item], dataMat[overLap,j]) #算出item和j的相似度
        #print 'the %d and %d similarity is: %f' % (item, j, similarity)
        simTotal += similarity
        ratSimTotal += similarity * userRating #加权，因为每个item用户的rating是不一样的
    if simTotal == 0: return 0
    else: return ratSimTotal/simTotal

def recommend(dataMat, user, N=3, simMeas=cosSim, estMethod=standEst):
    unratedItems = nonzero(dataMat[user,:].A==0)[1]
    if len(unratedItems) == 0: return 'you rated everything'
    itemScores = []
    for item in unratedItems: #找出每个item和user的关系
        estimatedScore = estMethod(dataMat, user, simMeas, item)
        itemScores.append((item, estimatedScore))
    return sorted(itemScores,key=lambda jj: jj[1], reverse=True)[:N] #取出topN，最相关的

其中求overLap的逻辑比较晦涩，

其中dataMat[:,item].A，找出item列，因为是matrix，用.A转成array

logical_and，其实就是找出最item列和j列都>0，只有都大于0才会是true

nonzero会给出其中不为0的index，对于二维的

>>> b2 = np.array([[True, False, True], [True, False, False]])
>>> np.nonzero(b2)
    (array([0, 0, 1]), array([0, 2, 0]))

所以知道b2[0,0]、b[0,2]和b2[1,0]的值不为0

最终取[0]，即取出user的index，哪些user同时评了item和j

因为是item-based，所以比较item的时候，维度就取决于user的个数，如果user很多，计算起来就比较麻烦

所以这里可以用SVD来降维，

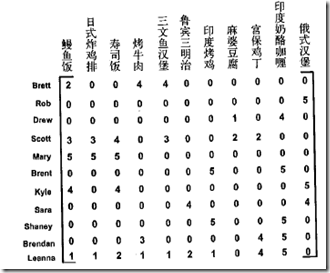
比如对如下的数据，

进行SVD分解，

>>>from numpy import linalg as la
>>> U,Sigma,VT=la.svd(mat(svdRec.loadExData2()))
>>> Sigma
array([ 1.38487021e+01, 1.15944583e+01, 1.10219767e+01,
        5.31737732e+00, 4.55477815e+00, 2.69935136e+00,
        1.53799905e+00, 6.46087828e-01, 4.45444850e-01,
        9.86019201e-02, 9.96558169e-17])

如何决定r？有个定量的方法是看多少个奇异值可以达到90%的能量

其实和PCA一样，由于奇异值其实是等于data×dataT特征值的平方根，所以总能量就是特征值的和

>>> Sig2=Sigma**2
>>> sum(Sig2)
541.99999999999932

而取到前4个时，发现超过90%，所以r=4

>>> sum(Sig2[:3])
500.50028912757909

所以SVD分解的版本的关键不同在于，降低了user的纬度，从n变为4

def svdEst(dataMat, user, simMeas, item):
    n = shape(dataMat)[1]
    simTotal = 0.0; ratSimTotal = 0.0
    U,Sigma,VT = la.svd(dataMat) #SVD分解
    Sig4 = mat(eye(4)*Sigma[:4]) #重构奇异矩阵
    xformedItems = dataMat.T * U[:,:4] * Sig4.I #构造item和user类的关系
    for j in range(n):
        userRating = dataMat[user,j]
        if userRating == 0 or j==item: continue
        similarity = simMeas(xformedItems[item,:].T,xformedItems[j,:].T)
        print 'the %d and %d similarity is: %f' % (item, j, similarity)
        simTotal += similarity
        ratSimTotal += similarity * userRating
    if simTotal == 0: return 0
    else: return ratSimTotal/simTotal

其中关键一步，

dataMat.T * U[:,:4] * Sig4.I

将dataMat基于特征向量旋转，再用特征值缩放，所以dataMat，m×n，转换为n×4的item和user类的矩阵

 

最后一个SVD的应用是图像压缩，

对于32×32，1024个像素的图片，进行SVD分解，如果取top 2的特征值，最终只需要保存32×2×2 +2 一共130个byte，比1024小了10倍