数字图像处理之傅里叶变换
by方阳
版权声明:本文为博主原创文章,转载请指明转载地址
http://www.cnblogs.com/fydeblog/p/7070055.html
1. 前言
这篇博客主要介绍常见的噪声及其概率密度函数,并用MATLAB复原函数对退化图像进行复原处理。这里复原是指在图像已经有噪声污染的情况下复原,与直接用傅里叶正反变换不一样!
2. 原理说明
(1) 常见噪声:椒盐噪声和高斯噪声
椒盐噪声是指两种噪声,一种是盐噪声,另一种是胡椒噪声。盐=白色,椒=黑色。前者是高灰度噪声,后者属于低灰度噪声。一般两种噪声同时出现,呈现在图像上就是黑白杂点。概率函数两极分化;
高斯噪声是指它的概率密度函数服从高斯分布(即正态分布)的一类噪声;
(2)图像复原是用去卷积函数实现的,用原图像卷积点扩散函数(点扩散函数即是一种运动模糊的算子),然后加入高斯噪声。然后用去卷积来恢复图像,有两种,一种不加入噪声估计,一种加入噪声估计,得到不同的恢复效果;
3. 实现内容
(1) 构造一个矩形方块图像,对其分别加入高斯和椒盐噪声,显示原始图像和噪声图像,及每个图片相对应的直方图。
(2) 任意选择一幅图像,对其使用运动模糊处理,再在模糊图像中加入高斯噪声,使用逆滤波和winner滤波对其进行去退化处理,比较效果,显示原始图像和复原图像。
4. 程序实现及实验结果
(1)噪声对图像直方图的影响
f(1000,1000)=0;
f=mat2gray(f);
[Y,X]=meshgrid(1:1000,1:1000);
f(1:500,1:500)=1;
f(500:1000,500:1000)=1;
I=f;
I1=imnoise(I,'salt & pepper',0.02);
I2=imnoise(I,'gaussian',0,0.01);
figure;
subplot(2,3,1);
imshow(I);
title('原图');
subplot(2,3,2);
imshow(I1);
title('椒盐噪声后的图像');
subplot(2,3,3);
imshow(I2);
title('高斯噪声后的图像');
subplot(2,3,4);
imhist(I);
title('原图直方图');
subplot(2,3,5);
imhist(I1);
title('椒盐噪声图像的直方图');
subplot(2,3,6);
imhist(I2);
title('高斯噪声图像的直方图');
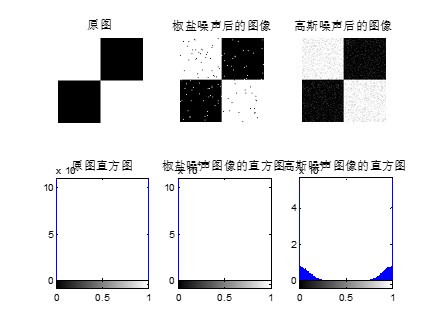
运行结果:
(2)逆滤波与winner滤波
I_1=imread('cameraman.tif');
PSF=fspecial('motion',21,11);
I3=imfilter(I_1,PSF,'conv','circular');
I3=imnoise(I3,'gaussian',0,0.0001);
I4=deconvwnr(I3,PSF);
I_1=im2double(I_1);
estimated_nsr=0.0001/var(I_1(:));
I5=deconvwnr(I3,PSF,estimated_nsr);
figure;
subplot(2,2,1);
imshow(I_1);
title('原图');
subplot(2,2,2);
imshow(I3);
title('模糊+噪声');
subplot(2,2,3);
imshow(I4);
title('逆滤波');
subplot(2,2,4);
imshow(I5);
title('winner滤波');
运行结果:

五. 结果分析
(1)从图1可以看出,原图(黑白图)直接是两极分化,加入椒盐噪声后直方图没有变化,因为椒盐噪声也是两极分化,加入高斯噪声可以看出直方图有高斯形状;
(2)从图2可以看出,用逆滤波出来的图像很不理想,用winner滤波出来的图像还行,看出图像恢复,信噪比是不可忽略的因素啊!