leedcode—problem861
rank:medium
1.问题
给定一个二维的矩阵(矩阵的数全由1和0组成),任意反转矩阵的每一行和每一列(0反转成1,1反转成0),求出最大矩阵分数,矩阵分数的求法是矩阵每一行代表二进制数,首位是最高位,根据二进制求出十进制,计算出每一行的十进制后,将所有十进制相加,返回结果,详细描述如图所示
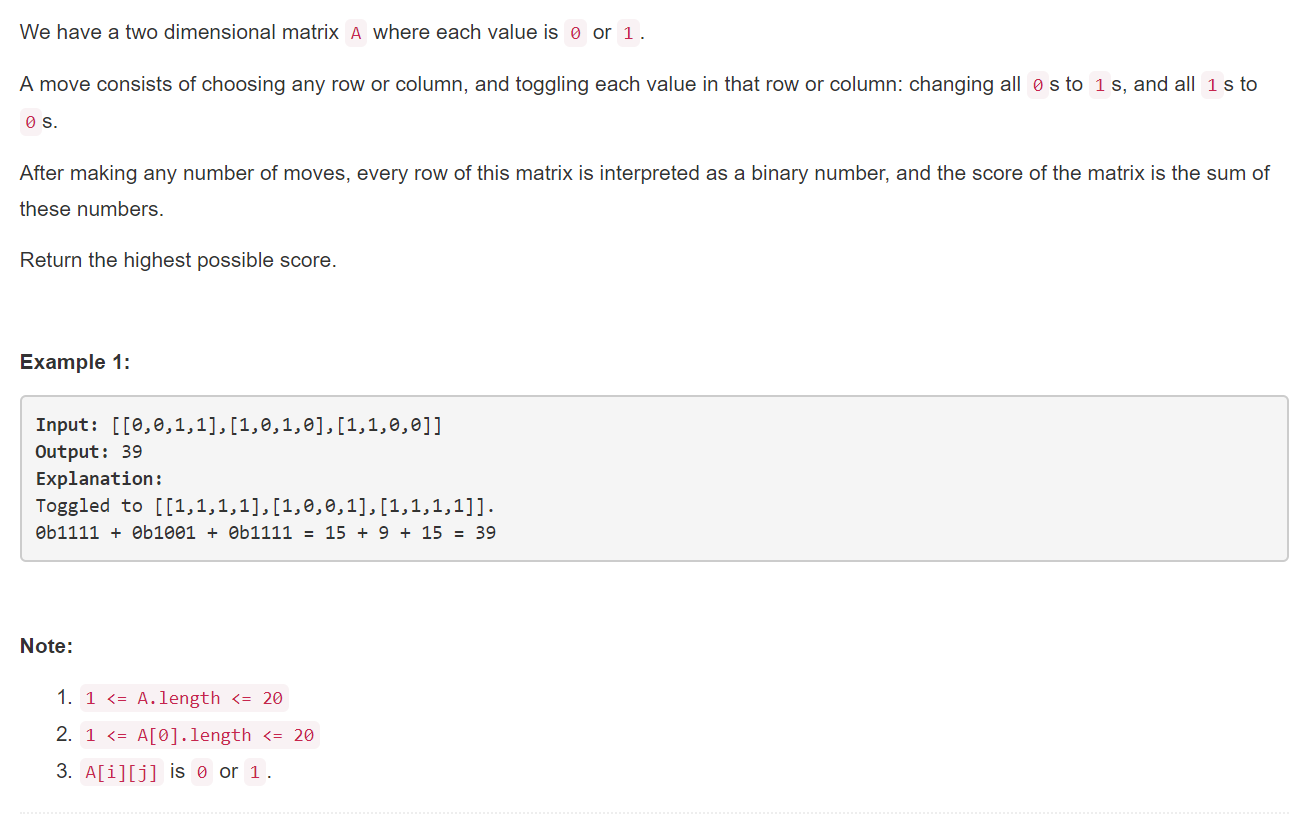
2.解决方案
1 class Solution: 2 def matrixScore(self, A): 3 """ 4 :type A: List[List[int]] 5 :rtype: int 6 """ 7 height = len(A) 8 width = len(A[0]) 9 10 def toggle_row(A, row): 11 for j in range(width): 12 if A[row][j]: 13 A[row][j] = 0 14 else: 15 A[row][j] = 1 16 return A 17 18 def toggle_column(A, column): 19 for i in range(height): 20 if A[i][column]: 21 A[i][column] = 0 22 else: 23 A[i][column] = 1 24 return A 25 26 def count_column_one(A, column): 27 num = 0 28 for i in range(height): 29 if A[i][column] == 1: 30 num += 1 31 return num 32 33 for i in range(height): 34 if A[i][0] == 0: 35 A = toggle_row(A, i) 36 37 for j in range(width-1): 38 num = count_column_one(A, j+1) 39 if num < height/2: 40 A = toggle_column(A,j+1) 41 from functools import reduce 42 result = 0 43 for i in range(height): 44 result += reduce(lambda x,y: x*2+y, A[i]) 45 return result
具体思路:首先我们要知道怎么能求出最大矩阵分数,一个二进制数,它的值大小,最高位是贡献最大(1/2值),比后面低位加起来贡献还大,所以要使这个二进制数尽可能大,最高位必须为1,也就是矩阵所有的行的第一位需置1,所以这里有一个toggle_row函数,用来反转行让首位置1。然后再是列反转,列反转的条件是在当前列,数字1的个数小于矩阵行数的1/2,则说明0的个数较多,反转列(使用toggle_column)将增大结果,依次循环第二列到最后一列即可。最后利用reduce函数求出每一行的结果并进行求和即可。
参考
1.https://leetcode.com/contest/weekly-contest-91/problems/score-after-flipping-matrix/