题目链接:
https://vjudge.net/problem/POJ-3041
题目大意:
给一个N*N的矩阵,有些格子有障碍,要求我们消除这些障碍,问每次消除一行或一列的障碍,
最少要几次。
解题思路:
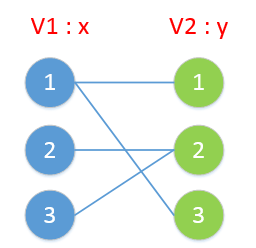
将每行、每列分别看作一个点,对于case的每一个行星坐标(x,y),将第x行和第y列连接起来,例如对于输入:
(1,1)、(1,3)、(2,2)、(3,2)4点构造图G:
这样,每个点就相当于图G的一条边,消灭所有点=消灭图G的所有边,又要求代价最少,即找到图G上的最少的点使得这些点覆盖了所有边。
根据定理吗, 最小点覆盖数=最大匹配数,所以本题转化为二分图的最大匹配问题——用匈牙利算法来解决。
1 #include<iostream> 2 #include<cstring> 3 using namespace std; 4 const int maxn = 500 + 10; 5 int n, m; 6 int Map[maxn][maxn];//map[i][j]=1表示X部的i和Y部的j存在路径 7 int cx[maxn], cy[maxn]; 8 bool vis[maxn]; 9 //cx[i]表示X部i点匹配的Y部顶点的编号 10 //cy[i]表示Y部i点匹配的X部顶点的编号 11 12 bool dfs(int u)//dfs进入的都是X部的点 13 { 14 for(int v = 1; v <= n; v++)//枚举Y部的点,判断X部的u和Y部的v是否存在路径 15 { 16 //如果存在路径并且还没被标记加入增广路 17 if(Map[u][v] && !vis[v])//vis数组只标记Y组 18 { 19 vis[v] = 1;//标记加入增广路 20 21 //如果Y部的点v还未被匹配 22 //或者已经被匹配了,但是可以从v点原来匹配的cy[v]找到一条增广路 23 //说明这条路就可是一个正确的匹配 24 if(cy[v] == -1 || dfs(cy[v])) 25 { 26 cx[u] = v;//可以匹配,进行匹配 27 cy[v] = u; 28 return 1; 29 } 30 } 31 } 32 return 0;//不能匹配 33 } 34 int maxmatch()//匈牙利算法主函数 35 { 36 int ans = 0; 37 memset(cx, -1, sizeof(cx)); 38 memset(cy, -1, sizeof(cy)); 39 for(int i = 1; i <= n; i++) 40 { 41 if(cx[i] == -1)//如果X部的i还未匹配 42 { 43 memset(vis, 0, sizeof(vis));//每次找增广路的时候清空vis 44 ans += dfs(i); 45 } 46 } 47 return ans; 48 } 49 int main() 50 { 51 cin >> n >> m; 52 int x, y; 53 for(int i = 0; i < m; i++) 54 { 55 cin >> x >> y; 56 Map[x][y] = 1; 57 } 58 cout<<maxmatch()<<endl; 59 }