A:最小排列
给定一个长度为m的序列b[1..m],再给定一个n,求一个字典序最小的1~n的排列A,使得b是A的子序列。
贪心即可,b是A的子序列,把不在b中的元素,从小到大放在队列中,再把b按顺序放入另一个队列中,每次取出两队列中较小值即可。
1 #include<bits/stdc++.h> 2 using namespace std; 3 typedef long long ll; 4 bool vis[100005]; 5 queue<int>q1, q2; 6 vector<int>ans; 7 int main() 8 { 9 int n, m, x; 10 cin >> n >> m; 11 for(int i = 0; i < m; i++)scanf("%d", &x), vis[x] = 1, q1.push(x); 12 for(int i = 1; i <= n; i++)if(!vis[i])q2.push(i); 13 while(!q1.empty() && !q2.empty()) 14 { 15 if(q1.front() > q2.front()) 16 { 17 ans.push_back(q2.front()); 18 q2.pop(); 19 } 20 else ans.push_back(q1.front()), q1.pop(); 21 } 22 while(!q1.empty())ans.push_back(q1.front()), q1.pop(); 23 while(!q2.empty())ans.push_back(q2.front()), q2.pop(); 24 for(int i = 0; i < ans.size(); i++) 25 printf("%d ", ans[i]); 26 return 0; 27 }
B:最大前缀和
给定一个长度为n的序列a[1..n],现在你可以进行最多k次操作,每次操作能交换序列中任意两个数,要求最大化最大前缀和的值。
最大前缀和的定义:

k最大为3
思路:
先求出前缀和,比如对于样例:
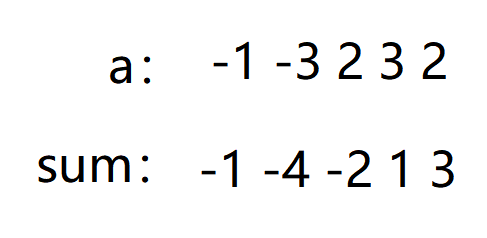
如果交换两个值a[l]和a[r],那么[l, r)的前缀和就加上a[r] - a[l]
如果要枚举l和r的话就达到n平方的复杂度,所以可以直接枚举sum数组
每次枚举一个前缀和,那么在前缀和包括的数字中选取一个最小值,不包括的数字中选取一个最大值,那么就可以直接求出该前缀和经过转化可以达到的最大值,可以用线段树查询区间最小值和最大值,时间复杂度O(nlog(n))
对于k=2的情况,一开始我以为是在k=1的解的情况下,交换那两个值,更新前缀和,再重新模拟一次,但是这样是错误的。
反例:
10 3
-10 9 -8 7 -6 5 -4 3 2 1
前缀和:-10 -1 -9 -2 -8 -3 -7 -4 -2 -1
在第一次循环找最大的前缀和时,找到交换的点是-10 和 7
7 9 -8 -10 -6 5 -4 3 2 1
前缀和 7 16 8 -2 -8 -3 -7 -4 -2 -1
最大前缀和为16
在此基础上第二次找到的最大前缀和是,交换-8 5
7 9 5 -10 -6 -8 -4 3 2 1
前缀和:7 16 21 11 5 -3 -7 -4 -2 -1
最大前缀和:21
在此基础上,第三次找最大前缀和,交换 -10 3
7 9 5 3 -6 -8 -4 -10 2 1
前缀和 7 16 21 24 18 10 6 -4 -2 -1
最大前缀和:24
但是正解应该是在最开始基础上用-10 -8 -6交换3 2 1
最开始:-10 9 -8 7 -6 5 -4 3 2 1
前缀和:-10 -1 -9 -2 -8 -3 -7 -4 -2 -1
正解:3 9 2 7 1 5 -4 -10 -8 -6
最大前缀和:27
那么之前的方法就不适用了吗?
不是的。
在k=1的时候,枚举每个前缀和,求出在前缀和中的数字最小值,和不在前缀和中数字的最大值。
那么k=2的时候,枚举每个前缀和,求出在前缀和中数字的最小和次小,和不在前缀的最大和次大,k=3时同理
那么还可以用线段树吗?
当然可以,在取出最小值时,把最小值的那个点更改成INF,再求最小值就是次小值了,同理可以求出。
线段树不熟练,代码啰嗦,这道题也可以直接用set模拟。
1 #include<bits/stdc++.h> 2 using namespace std; 3 typedef long long ll; 4 const int maxn = 1000000+10; 5 #define MID(l, r) ((l) + ((r) - (l)) / 2) 6 #define lc ((o)<<1) 7 #define rc ((o)<<1|1) 8 ll a[maxn]; 9 struct node 10 { 11 ll l, r, mmax, mmin, idmin, idmax; 12 }tree[maxn]; 13 void pushup(int o) 14 { 15 if(tree[lc].mmax > tree[rc].mmax) 16 { 17 tree[o].mmax = tree[lc].mmax; 18 tree[o].idmax = tree[lc].idmax; 19 } 20 else 21 { 22 tree[o].mmax = tree[rc].mmax; 23 tree[o].idmax = tree[rc].idmax; 24 } 25 if(tree[lc].mmin > tree[rc].mmin) 26 { 27 tree[o].mmin = tree[rc].mmin; 28 tree[o].idmin = tree[rc].idmin; 29 } 30 else 31 { 32 tree[o].mmin = tree[lc].mmin; 33 tree[o].idmin = tree[lc].idmin; 34 } 35 } 36 void build(ll o, ll l, ll r) 37 { 38 tree[o].l = l, tree[o].r = r; 39 if(l == r) 40 { 41 tree[o].mmax = tree[o].mmin = a[l]; 42 tree[o].idmin = tree[o].idmax = l; 43 return; 44 } 45 ll m = MID(l, r); 46 build(lc, l, m); 47 build(rc, m + 1, r); 48 pushup(o); 49 //cout<<o<<" "<<l<<" "<<r<<" "<<tree[o].mmax<<" "<<tree[o].mmin<<endl; 50 } 51 ll ql, qr;//查询区间[ql, qr]中的max,min 52 ll ans_max, ans_min; 53 ll max_id, min_id; 54 void query(int o) 55 { 56 if(ql <= tree[o].l && qr >= tree[o].r)//[L, R]包含在[ql, qr]区间内,直接用该节点的信息,达到线段树查询快的操作 57 { 58 if(ans_max < tree[o].mmax) 59 { 60 ans_max = tree[o].mmax; 61 max_id = tree[o].idmax; 62 } 63 if(ans_min > tree[o].mmin) 64 { 65 ans_min = tree[o].mmin; 66 min_id = tree[o].idmin; 67 } 68 return; 69 } 70 int m = MID(tree[o].l, tree[o].r); 71 if(ql <= m)query(lc); 72 if(qr > m)query(rc); 73 } 74 //单点更新,a[p] = v; 75 ll p, v; 76 void update(ll o) 77 { 78 if(tree[o].l == tree[o].r) 79 { 80 tree[o].mmax = v; 81 tree[o].mmin = v; 82 return; 83 } 84 ll m = MID(tree[o].l, tree[o].r); 85 if(p <= m)update(lc); 86 else update(rc); 87 pushup(o); 88 } 89 90 ll sum[maxn]; 91 ll INF = 1e18 + 7; 92 int main() 93 { 94 ll n, k; 95 scanf("%lld%lld", &n, &k); 96 97 ll MAX = -INF, L = 0, R = 0, c = 0; 98 for(int i = 1; i <= n; i++) 99 { 100 scanf("%lld", &a[i]); 101 sum[i] = sum[i - 1] + a[i]; 102 MAX = max(MAX, sum[i]); 103 } 104 build(1, 1, n); 105 106 ll lid[4], lmin[4], rid[4], rmax[4]; 107 for(int i = k; i < n - k + 1; i++) 108 { 109 for(int j = 1; j <= k; j++) 110 { 111 ans_min = INF; 112 ql = 1, qr = i, query(1); 113 lid[j] = min_id, lmin[j] = ans_min; 114 p = min_id, v = INF, update(1); 115 116 ans_max = -INF; 117 ql = i + 1, qr = n, query(1); 118 rid[j] = max_id, rmax[j] = ans_max; 119 p = max_id, v = -INF, update(1); 120 //cout<<i<<endl; 121 //cout<<lid<<" "<<lmin<<" "<<rid<<" "<<rmax<<endl; 122 } 123 ll l = 0, r = 0; 124 for(int j = 1; j <= k; j++) 125 { 126 l += lmin[j]; 127 r += rmax[j]; 128 p = lid[j], v = lmin[j], update(1); 129 p = rid[j], v = rmax[j], update(1); 130 } 131 if(sum[i] + r - l > MAX) 132 { 133 MAX = sum[i] + r - l; 134 } 135 } 136 cout<<MAX<<endl; 137 return 0; 138 }
集合的写法:
1 #include<bits/stdc++.h> 2 using namespace std; 3 typedef long long ll; 4 const int maxn = 1e6 + 10; 5 const int mod = 1e9 + 7; 6 7 set<int>lmin, rmax; 8 map<int, int>lnum, rnum; 9 void add(set<int>&a, map<int, int>&b, int x)//在可重复集合中加入x 10 { 11 a.insert(x); 12 b[x]++; 13 } 14 void sub(set<int>&a, map<int, int>&b, int x)//在可重复集合中删除x 15 { 16 b[x]--; 17 if(b[x] == 0)a.erase(a.find(x)); 18 } 19 int Find(set<int>&a, map<int, int>&b, bool flag)//在可重复集合中取出最小值 最大值 20 { 21 set<int>::iterator it; 22 int ans; 23 if(flag)//取出最小值 24 { 25 it = a.begin(); 26 ans = *it; 27 b[ans]--; 28 if(b[ans] == 0)a.erase(it); 29 } 30 else 31 { 32 it = a.end(); 33 it--; 34 ans = *it; 35 b[ans]--; 36 if(b[ans] == 0)a.erase(it); 37 } 38 return ans; 39 } 40 int a[50005], b[10], c[10]; 41 int main() 42 { 43 int n, k; 44 cin >> n >> k; 45 for(int i = 1; i <= n; i++) 46 cin >> a[i]; 47 ll sum = 0, ans = 0; 48 for(int i = 1; i <= k; i++)add(lmin, lnum, a[i]), sum += a[i]; 49 ans = sum; 50 for(int i = k + 1; i <= n; i++)add(rmax, rnum, a[i]); 51 for(int i = k + 1; i <= n - k + 1; i++) 52 { 53 ll tot = 0; 54 for(int j = 1; j <= k; j++)b[j] = Find(lmin, lnum, 1);//在前缀集合中取出前k小 55 for(int j = 1; j <= k; j++)c[j] = Find(rmax, rnum, 0);//在非前缀集合中取出前k大 56 for(int j = 1; j <= k; j++)tot = tot + c[j] - b[j];//计算差值 57 ans = max(ans, sum + tot);//更新答案 58 sum += a[i];//更新答案 59 for(int j = 1; j <= k; j++)//将取出的数字放回去 60 { 61 add(lmin, lnum, b[j]); 62 add(rmax, rnum, c[j]); 63 } 64 add(lmin, lnum, a[i]);//前缀加上该点 65 sub(rmax, rnum, a[i]);//非前缀删除该点 66 } 67 cout<<ans<<endl; 68 return 0; 69 }
C:质数
我们称一个数是好的数,当且仅当他可以写成质数个质数的乘积。
现在给定l,r,求[l,r]内有几个好的数。第一行两个正整数l,r,满足1 ≤ l ≤ r ≤ 109,且0 ≤ r-l ≤ 106。
思路:
直接用素数线性筛法,筛选小素数的时候,把l-r区间中该素数的倍数过一遍,求出每个数的分解式中该素数的指数,最后就可以求出这个区间中的每一个数字由x个素数相乘,再判断这个x是不是素数即可
1 #include<bits/stdc++.h> 2 using namespace std; 3 typedef long long ll; 4 const int maxn = 1000000+10; 5 int is_prime[maxn], tot[maxn];//这是ab区间上的素数 6 bool is_prime_small[maxn];//这是(2,根号b)区间的素数 7 int sum_prime(ll a, ll b)//[a, b]区间内素数筛选 8 { 9 for(ll i = 0; i * i <= b; i++)is_prime_small[i] = 1; 10 is_prime_small[0] = is_prime_small[1] = 0; 11 for(ll i = 0; i <= b - a; i++)is_prime[i] = i + a; 12 for(ll i = 2; i * i <= b; i++) 13 { 14 if(is_prime_small[i])//如果是小区间上的素数那就直接筛选小区间和大区间 15 { 16 for(ll j = 2 * i; j * j <= b; j += i)is_prime_small[j] = 0;//筛选小区间 17 18 for(ll j = max(2LL, (a + i - 1) / i) * i; j <= b; j += i)//j初始化的时候是ab区间中第一个i的倍数 19 { 20 //cout<<j<<" "<<i<<" "<<is_prime[j - a]<<endl; 21 while(is_prime[j - a] % i == 0) 22 { 23 is_prime[j - a] /= i; 24 tot[j - a]++; 25 } 26 } 27 } 28 } 29 int sum = 0; 30 for(ll i = 0; i <= b - a; i++)if(is_prime[i] != 1)tot[i]++; 31 for(ll i = 0; i <= b - a; i++)if(is_prime_small[tot[i]])sum++; 32 return sum; 33 } 34 35 int main() 36 { 37 //freopen("out.txt", "w", stdout); 38 int a, b; 39 cin >> a >> b; 40 cout<<sum_prime(a, b)<<endl;; 41 return 0; 42 }
D: 随机排列2
一个长度为n的排列p[1..n]的价值是这样定义的:一开始你有一个数x,x的值一开始为0,然后对于1 ≤ i ≤ n,如果p[i] > x,则令x=p[i];排列p[1..n]的价值就是x的值的改变次数。
求对于所有长度为n的[1,2…n]的排列,他们的价值之和,答案对109+7取模。
找规律:
n比较小的时候先算出答案
n = 1 ans = 1
n = 2 ans = 3
n = 3 ans = 11
n = 4 ans = 50
感觉没什么规律。
首先对于1-n的排列中,如果n是第一个,那么x值的改变次数就是1,这种情况有(n - 1)!种情况
那就把答案先加上n - 1的阶乘
用上面的总数减去(n - 1)!看看还差多少
n = 1 ans = 0! + 0 = 1
n = 2 ans = 1! + 2 = 3
n = 3 ans = 2! + 9 = 11
n = 4 ans = 3! + 44 = 50
感觉有点规律:
上述同色的数字中:
2 = 2 * 1
9 = 3 * 3
44 = 4 * 11
可以推出规律:a[n] = (n - 1)! + n * a[n - 1]
下面来解释一下这个式子
首先对于(n - 1)!这个没什么好说的,就是n为首位的排列数目
那么n*a[n - 1]是怎么来的呢,其实这里我也证明不了,只是找规律发现的
下面举个例子
a[3] = 9
那么3的全排列为 1 2 3 、1 3 2 、2 1 3、2 3 1、3 1 2、3 2 1
那么在这个基础上放4,这里4不放在首位,因为放在首位的已经在(n - 1)!计算过了。(请看下图)
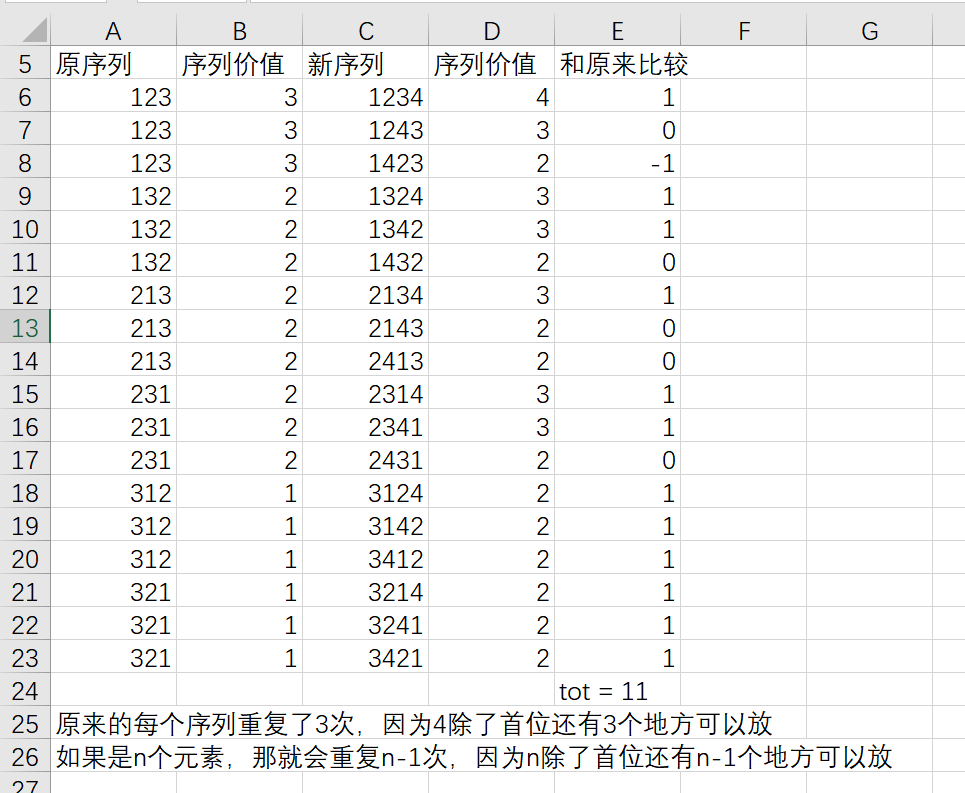
首先找到规律发现,加入4之后,序列和原来序列相比多了11,就等于a[3]
而且原来的序列重复了3次,那么价值就是3*a[3]
上面两个加起来就是4*a[3]
所以a[4] = 3! + 4 * a[3]
对于a[n]的话也是这样的,n-1的序列会重复n-1次,这里就加上了(n - 1) * a[n - 1]
而且最终的每个序列和原来相比总增加量也为a[i](这里只是发现的规律,至于为什么增加这么多我也不知道)
a[n] = (n - 1)! + n * a[n - 1]
知道了这个规律就可以直接写代码了
1 #include<bits/stdc++.h> 2 using namespace std; 3 typedef long long ll; 4 const int maxn = 1e6 + 10; 5 const int mod = 1e9 + 7; 6 ll a[maxn]; 7 int main() 8 { 9 ll p = 1; 10 a[1] = 1; 11 for(int i = 2; i < maxn; i++) 12 { 13 p = p * (i - 1) % mod;//p表示(i - 1)的阶乘 14 a[i] = p + i * a[i - 1]; 15 a[i] %= mod; 16 } 17 int n; 18 cin >> n; 19 cout<<a[n]<<endl; 20 return 0; 21 }