hOmewOrk 第三单元 总结
JML理论基础梳理
JML是用于对Java程序进行规格化设计的一种表示语言。
1. 注释结构
JML表示规格的内容包含在注释之中。可以使用行注释和块注释。行注释的表示方式为 //@annotation ,块注释的方式为 /* @ annotation @*/ 。
2. JML表达式
JML表达式是在基于JAVA语法基础上,新增了一些操作符和和原子表达式组成的。
2.1 原子表达式
esult表达式:表示方法执行后的返回值。
old( expr )表达式:用来表示一个表达式 expr 在相应方法执行前的取值。
ot_assigned(x,y,...)表达式:用来表示括号中的变量是否在方法执行过程中被赋值。
ot_modified(x,y,...)表达式:与上面的 ot_assigned表达式类似,该表达式限制括号中的变量在方法执行期间的取 值未发生变化。
onnullelements( container )表达式:表示 container 对象中存储的对象不会有 null。
ype(type)表达式:返回类型type对应的类型(Class)。
ypeof(expr)表达式:该表达式返回expr对应的准确类型。
2.2 量化表达式
forall表达式:全称量词修饰的表达式,表示对于给定范围内的元素,每个元素都满足相应的约束。
exists表达式:存在量词修饰的表达式,表示对于给定范围内的元素,存在某个元素满足相应的约束。
sum表达式:返回给定范围内的表达式的和。
product表达式:返回给定范围内的表达式的连乘结果。
max表达式:返回给定范围内的表达式的最大值。
min表达式:返回给定范围内的表达式的最小值。
um_of表达式:返回指定变量中满足相应条件的取值个数。
2.3 集合表达式
集合构造表达式:可以在JML规格中构造一个局部的集合(容器),明确集合中可以包含的元素。
2.4 操作符
(1) 子类型关系操作符: E1<:E2 ,如果类型E1是类型E2的子类型(sub type),则该表达式的结果为真,否则为假。
(2) 等价关系操作符: b_expr1<==>b_expr2 或者 b_expr1<=!=>b_expr2 ,其中b_expr1和b_expr2都是布尔表达 式,这两个表达式的意思是 b_expr1==b_expr2 或者 b_expr1!=b_expr2 。
(3) 推理操作符: b_expr1==>b_expr2 或者 b_expr2<==b_expr1 。对于表达式 b_expr1==>b_expr2 而言,当 b_expr1==false ,或者 b_expr1==true 且 b_expr2==true 时,整个表达式的值为 true
3. 方法规格
前置条件(pre-condition):前置条件通过requires子句来表示: requires P; 。其中requires是JML关键词,表达的意思是“要求调用者确保P为 真”。
后置条件(post-condition):后置条件通过ensures子句来表示: ensures P; 。其中ensures是JML关键词,表达的意思是“方法实现者确保方法执 行返回结果一定满足谓词P的要求,即确保P为真”。
副作用范围限定(side-effects):副作用指方法在执行过程中会修改对象的属性数据或者类的静态成员数据,从而给后续方法的执行带来影响。从方法 规格的角度,必须要明确给出副作用范围。
4. 类型规格
类型规格指针对Java程序中定义的数据类型所设计的限制规则。
不变式invariant:不变式(invariant)是要求在所有可见状态下都必须满足的特性。
状态变化约束constraint:对前序可见状态和当前可见状态的关系进行约束。
JML应用工具链
openJML:检测JML的语法和规格
JUnit4:对于类进行检测
openJML自动生成测试用例
测试代码如下
public class fu:
{
/*@ public normal_behaviour
@ ensures
esult == lhs - rhs;
*/
public int c(int lhs, int rhs)
{
return lhs - rhs;
}
public static void main(String args)
{
c(114514,1919810);
}
}
测试显示正确:

代码中把JML的减号改为加号:
public class fu
{
/*@ public normal_behaviour
@ ensures
esult == lhs + rhs;
*/
public int c(int lhs, int rhs)
{
return lhs - rhs;
}
public static void main(String args)
{
c(114514,1919810);
}
}
测试结果如下:
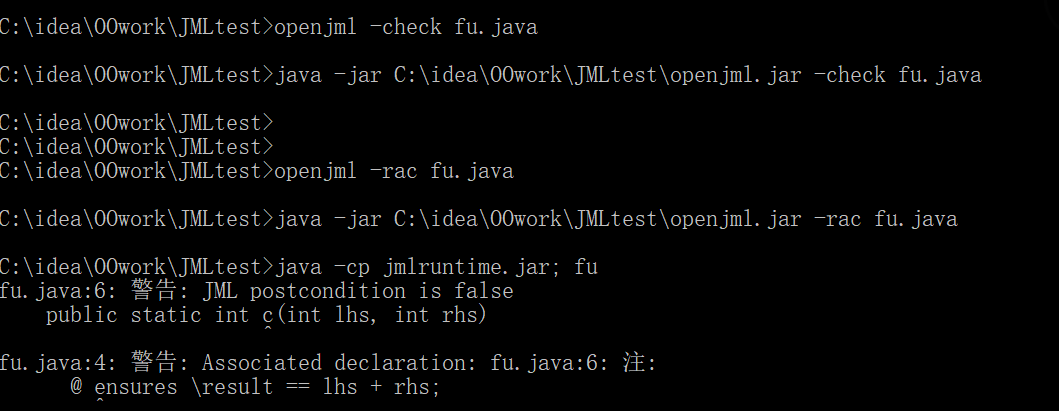
openJML检测出了JML的问题。
架构设计分析
第一次作业
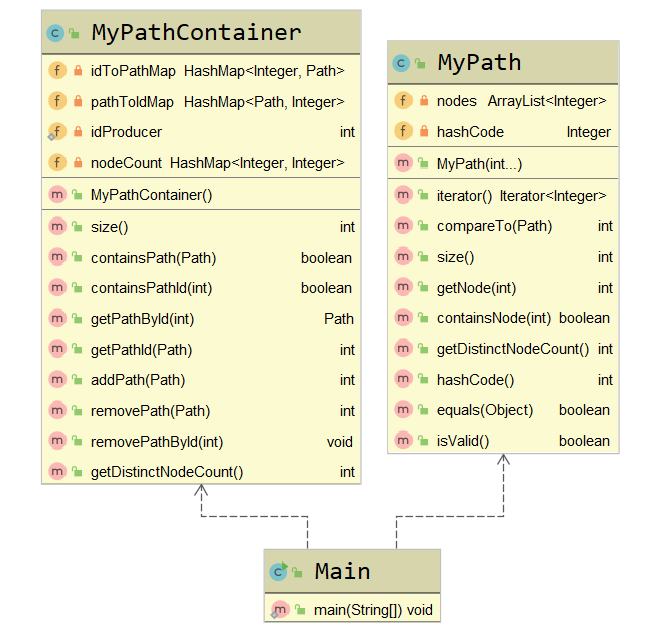
MyPath类中适用一个ArrayList,保存所有的节点编号。
值得注意的是,我重写了hashCode方法:
@Override
public int hashCode()
{
if (hashCode == null)
{
hashCode = nodes.hashCode();
}
return hashCode;
}
其中的nodes,是类中nodes的hashCode。这个设计避免了原有的hashcode的O(n),又可以不自己编写哈希码的生成算法。
MyPathContainer类没有适用JML中给的静态数组的数据结构,而是使用了idToPathMap和pathToIdMap这两个HashMap,分别储存路径id到路径,路径到路径id。这样的好处是,从一者查询另一者就不需要遍历查询,而是直接O(1),提升了效率。
其中nodeCount这个hashmap数据结构,储存了Node到路径出现次数,是专门为实现查询容器全局范围内不同节点的数量的。在add和remove维护nodeCount,在调用getDistinctNodeCount方式时候就可以直接O(1)查询,大大减少了非变更性指令的执行时间。
public /*@pure@*/int getDistinctNodeCount() //在容器全局范围内查找不同的节点数
{
return nodeCount.size();
}
第二次作业
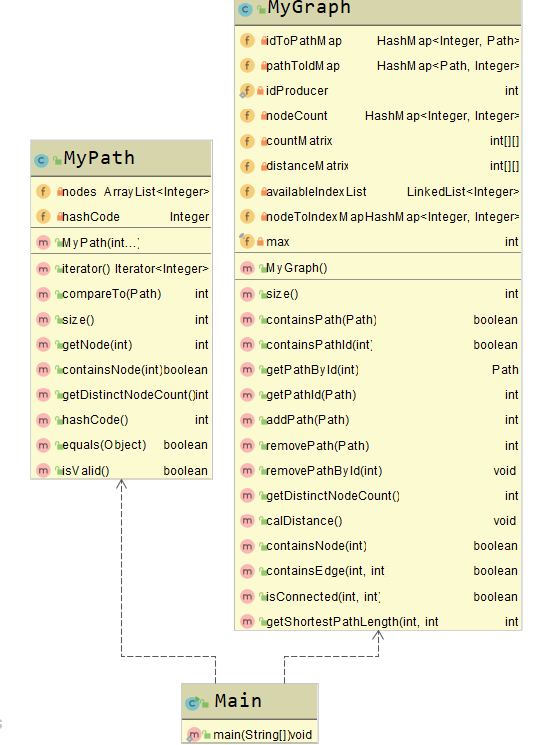
本次作业中MyPath类没有变化,在MyPathContainer类基础上写了MyGraph类。为什么不继承呢?因为checkstyle不允许适用protected权限的变量,所以继承就无从谈起!这个为了规范代码风格的插件居然影响了OOP最重要的继承特性,真是让人失望。
言归正传,本次作业最核心也是最困难的函数就是计算最短路径,可以计算最短路径,也就容易判断是否连通了。
所以,我设计了两个静态二维数组:countMatrix用来记录每条边出现的次数,disatanceMatrix用来记录点和点之间的最短路径。每次增/删边的时候,更新countMatrix,再根据countMatrix,适用Floyd计算各个点之间距离,写入disatanceMatrix(对于不连通的点赋值为999999)。
在判断是否连通时,判断路径长度是否>250,>250就是不连通。
在计算最短路径时,直接读取disatanceMatrix,复杂度为O(1).
此方案中还有一个有意思的设计。读入的nodeId和disatanceMatrix,countMatrix中数组下标并不一致,但是存在一一映射关系。所以,我借鉴OS中空闲物理页表和虚拟页表分配的想法,建立了“空闲数组下标链表”:availbleIndexList。当增加新Node时从中poll一个空闲数组下标,删除Node时候又将其释放后放入availbleIndexList。
第三次作业
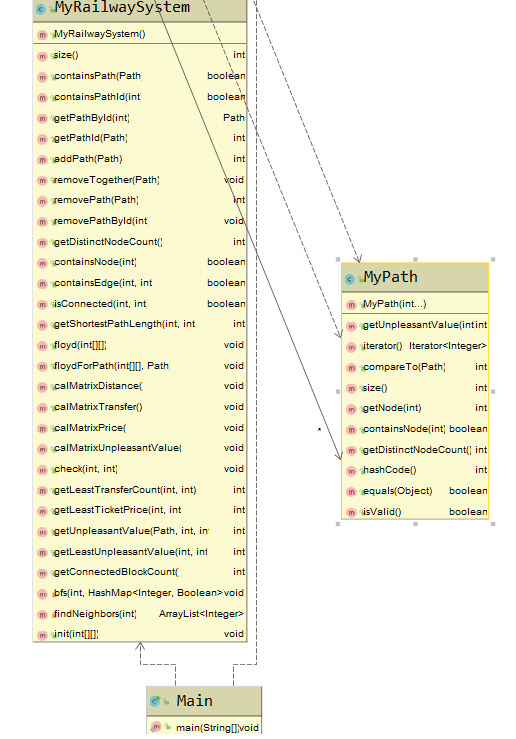
这次作业的依然没有采用继承的良好设计(还是因为checkstyle)。所以在图中可以看出,MyRailwaySystem类异常冗长。这确实非常无奈。
此次作业我采用了讨论区中”权转换“的方法(完全相同)
方法参见:https://course.buaaoo.top/assignment/75/discussion/213
这位老哥的方法非常之强,把动态权图问题转化为静态权图问题。所以依然可以用Floyd快乐暴力解决。与第二次作业中记录最短路径的数组类似,本次作业新增了这三个数据结构:
private int[][] matrixTransfer = new int[120][120]; //记录最短换乘
private int[][] matrixPrice = new int[120][120]; //记录最少票价
private int[][] matrixUnpleasantValue = new int[120][120]; //记录最少不满意度
对于matrixTransfer的更新十分简单:直接遍历现有的所有path,每条path都赋值。一条path上赋值为1,注意其中相同节点赋值为0。
对于matrixPrice和matrixUnpleasantValue的更新比较麻烦:对于所有path,先要在本path内赋值完相邻节点后Floyd。最后所有path赋值完成后,再次全图Floyd。
对于计算连通块getConnectedBlockCount(),我用了BFS:从一个节点出发广度优先遍历,能找到的点都设置为“已访问”,计数器+1。再在未访问的点中选一个点,重复以上过程,直到所有点都已经被访问过。计数器的值即为连通块数。
bug修复情况
很遗憾,这三次作业中在强测和互测中都没有出现bug。
关于规格撰写和理解的心得体会
1.JML提供了契约式编程的良好方式,让设计和代码实现分离开来。这样一来,就迫使设计者在工程一开始就想明白应该如何设计,而不是在之后修修补补。JML也让debug更加容易:在各个方法的层次上就可以进行验证正确性,最后整个工程的正确性检验又可以转变为各个方法互相调用的正确性检验。
2.JML的检测使用起来不容易,对于一个方法的检测需要的精力甚至要高于编写这个方法的精力。从效用比上来说,传统的调试方法更加高效。
3.JML不便于阅读和编写。课程组在JML的编写上尚会出现失误,那对我们这样水平的初学者来说更是困难。而且JML阅读也十分晦涩,第三次作业我甚至没有看JML,直接根据指导书描述写了作业。JML虽然精确,但是对于相对复杂的方法而言,自然语言也不失为一个选择。