深度优先搜索

深度优先搜索（DFS：Depth-First Search）是一种图搜索策略，其将搜索限制到 2 种操作：

• (a) 访问图中的一个节点；
• (b) 访问该节点的子节点；

在深度优先搜索中，对于最新发现的顶点，如果它还有以此为起点而未探测到的边，就沿此边继续探测下去。当顶点 v 的所有边都已被探寻过后，搜索将回溯到发现顶点 v 有起始点的那些边。这一过程一直进行到已发现从源顶点可达的所有顶点为止。实际上深度优先搜索最初的探究也是为了解决迷宫问题。

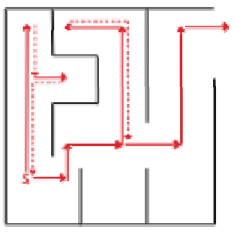
对图的深度优先搜索与对树（Tree）的深度优先遍历（Depth First Traversal）是类似的，区别在于图中可能存在环，所以可能会遍历到已经遍历的节点。

例如，下面的图中，从顶点 2 开始遍历，当遍历到顶点 0 时，子顶点为 1 和 2，而顶点 2 已经遍历过，如果不做标记，遍历过程将陷入死循环。所以，在 DFS 的算法实现中需要对顶点是否访问过做标记。

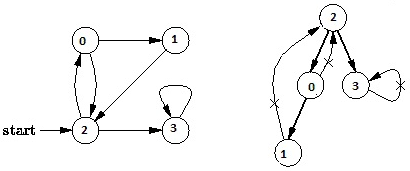
上图的 DFS 遍历结果为 2, 0, 1, 3。

DFS 算法可以通过不同方式来实现：

• 递归方式
• 非递归方式：使用栈（Stack）数据结构来存储遍历图中节点的中间状态；

DFS 算法的递归方式伪码如下：

procedure DFS(G,v):
    label v as discovered
    for all edges from v to w in G.adjacentEdges(v) do
        if vertex w is not labeled as discovered then
            recursively call DFS(G,w)

DFS 算法的非递归方式伪码如下：

procedure DFS-iterative(G,v):
    let S be a stack
    S.push(v)
    while S is not empty
          v ← S.pop() 
          if v is not labeled as discovered:
              label v as discovered
              for all edges from v to w in G.adjacentEdges(v) do
                  S.push(w)

深度优先搜索（DFS）的时间复杂度为 O(V+E)，V 即 Vertex 顶点数量，E 即 Edge 边数量。

DFS 算法实现代码如下：

using System;
using System.Linq;
using System.Collections.Generic;

namespace GraphAlgorithmTesting
{
  class Program
  {
    static void Main(string[] args)
    {
      Graph g = new Graph(4);
      g.AddEdge(0, 1);
      g.AddEdge(0, 2);
      g.AddEdge(1, 2);
      g.AddEdge(2, 0);
      g.AddEdge(2, 3);
      g.AddEdge(3, 3);

      foreach (var vertex in g.DFS(2))
      {
        Console.WriteLine(vertex);
      }
      foreach (var vertex in g.RecursiveDFS(2))
      {
        Console.WriteLine(vertex);
      }

      Console.ReadKey();
    }

    class Edge
    {
      public Edge(int begin, int end)
      {
        this.Begin = begin;
        this.End = end;
      }

      public int Begin { get; private set; }
      public int End { get; private set; }
    }

    class Graph
    {
      private Dictionary<int, List<Edge>> _adjacentEdges
        = new Dictionary<int, List<Edge>>();

      public Graph(int vertexCount)
      {
        this.VertexCount = vertexCount;
      }

      public int VertexCount { get; private set; }

      public void AddEdge(int begin, int end)
      {
        if (!_adjacentEdges.ContainsKey(begin))
        {
          var edges = new List<Edge>();
          _adjacentEdges.Add(begin, edges);
        }

        _adjacentEdges[begin].Add(new Edge(begin, end));
      }

      public List<int> DFS(int start)
      {
        List<int> traversal = new List<int>();
        int current = start;

        // mark all the vertices as not visited
        bool[] visited = new bool[VertexCount];
        for (int i = 0; i < VertexCount; i++)
        {
          visited[i] = false;
        }

        // create a stack for DFS
        Stack<int> stack = new Stack<int>();

        // mark the current node as visited and push it
        visited[current] = true;
        stack.Push(current);

        while (stack.Count > 0)
        {
          current = stack.Pop();

          // if this is what we are looking for
          traversal.Add(current);

          // get all child vertices of the popped vertex,
          // if a child has not been visited, 
          // then mark it visited and push it
          if (_adjacentEdges.ContainsKey(current))
          {
            foreach (var edge in _adjacentEdges[current].OrderByDescending(e => e.End))
            {
              if (!visited[edge.End])
              {
                visited[edge.End] = true;
                stack.Push(edge.End);
              }
            }
          }
        }

        return traversal;
      }

      public List<int> RecursiveDFS(int start)
      {
        List<int> traversal = new List<int>();
        int current = start;

        // mark all the vertices as not visited
        bool[] visited = new bool[VertexCount];
        for (int i = 0; i < VertexCount; i++)
        {
          visited[i] = false;
        }

        // traversal
        RecursiveDFSTraversal(current, visited, traversal);

        return traversal;
      }

      private void RecursiveDFSTraversal(int current, bool[] visited, List<int> traversal)
      {
        visited[current] = true;
        traversal.Add(current);

        if (_adjacentEdges.ContainsKey(current))
        {
          foreach (var edge in _adjacentEdges[current].OrderBy(e => e.End))
          {
            if (!visited[edge.End])
            {
              RecursiveDFSTraversal(edge.End, visited, traversal);
            }
          }
        }
      }
    }
  }
}

参考资料

• 广度优先搜索
• 深度优先搜索
• Breadth First Traversal for a Graph
• Depth First Traversal for a Graph
• 深度优先搜索 广度优先搜索类训练题
• Introduction to Algorithms 6.006 - Lecture 13
• 深度优先搜索 DFS
• 算法与数据结构

本篇文章《深度优先搜索》由 Dennis Gao 发表自博客园，未经作者本人同意禁止任何形式的转载，任何自动或人为的爬虫转载行为均为耍流氓。