八皇后问题

八皇后问题是数学家高斯于1850年提出的，这是一个典型的回溯算法的问题。八皇后问题的大意如下：

　　国际象棋的棋盘有8行8列共64个单元格，在棋盘上摆放8个皇后，使其不能互相攻击，也就是说任意两个皇后都不能处于同一行、同一列或同一斜线上。问总共共有多少种摆放方法，每一种摆放方式是怎样的。

　　目前，数学上可以证明八皇后问题总共有92种解。

1. 八皇后问题算法

首先来分析八皇后问题，这个问题的关键是，8个皇后中任意两个皇后都不能处于同一行、同一列或同一斜线上。可以采用递归的思想来求解八皇后问题，算法的设计思路如下：

（1）首先在棋盘的某个位置放置一个皇后。

（2）然后，放置下一个皇后。

（3）此时，判断该皇后是否与前面已有皇后形成互相攻击，若不形成互相攻击，则重复第二个步骤，继续放置下一列的皇后。

（4）当放置完8个不形成攻击的皇后，就找到一个解，将其输出。

这里可以使用递归的方式来实现。可以按照此思路来编写相应的八皇后问题的求解算法，代码示例如下：

    static int iCount=0;    //全局变量
    static int[] WeiZhi=new int[8];    //全局数组
    static void Output(){
        int i,j,flag=1;
        System.out.printf("第%2d种方案(★表示皇后):
", ++iCount);    //输出序号
        System.out.printf("     ");
        for(i=1;i<=8;i++){
            System.out.print("▁");
        }
        System.out.println();
        for(i=0;i<8;i++){
            System.out.print("▕");
            for(j=0;j<8;j++){
                if(WeiZhi[i]-1==j){
                    System.out.print("★");    //皇后的位置
                }else{
                    if(flag<0){
                        System.out.print("     ");    //棋格
                    }else{
                        System.out.print("■");    //棋格
                    }
                }
                flag=-1*flag;
            }
            System.out.println("▏ " );
            flag=-1*flag;
        }
        System.out.print("     ");
        for(i=1;i<=8;i++){
            System.out.print("▔");
        }
        System.out.println();
    }
    
    //算法
    static void eightQueen(int n){
        int i,j;
        int ct;    //用于判断是否冲突
        if(n==8){
            Output();    //输出求解结果
            return;
        }
        for(i=1;i<=8;i++){    //试探
            WeiZhi[n]=i;    //在该列的第i行上放置
            //判断第n个皇后是否与前面的皇后形成攻击
            ct=1;
            for(j=0;j<n;j++){
                if(WeiZhi[n]==WeiZhi[j]){    //形成攻击
                    ct=0;
                }else if(Math.abs(WeiZhi[j]-WeiZhi[n])==(n-j)){    //形成攻击
                    ct=0;
                }else{
                    
                }
            }
            if(ct==1)    //没有冲突，就开始下一列的试探
                eightQueen(n+1);    //递归调用
        }
    }

2. 八皇后问题求解

完整的八皇后求解程序代码如下：

package com.cn.suanfaquti;

public class EightQueen {
    static int iCount=0;    //全局变量
    static int[] WeiZhi=new int[8];    //全局数组
    static void Output(){
        int i,j,flag=1;
        System.out.printf("第%2d种方案(★表示皇后):
", ++iCount);    //输出序号
        System.out.printf("     ");
        for(i=1;i<=8;i++){
            System.out.print("▁");
        }
        System.out.println();
        for(i=0;i<8;i++){
            System.out.print("▕");
            for(j=0;j<8;j++){
                if(WeiZhi[i]-1==j){
                    System.out.print("★");    //皇后的位置
                }else{
                    if(flag<0){
                        System.out.print("     ");    //棋格
                    }else{
                        System.out.print("■");    //棋格
                    }
                }
                flag=-1*flag;
            }
            System.out.println("▏ " );
            flag=-1*flag;
        }
        System.out.print("     ");
        for(i=1;i<=8;i++){
            System.out.print("▔");
        }
        System.out.println();
    }
    
    //算法
    static void eightQueen(int n){
        int i,j;
        int ct;    //用于判断是否冲突
        if(n==8){
            Output();    //输出求解结果
            return;
        }
        for(i=1;i<=8;i++){    //试探
            WeiZhi[n]=i;    //在该列的第i行上放置
            //判断第n个皇后是否与前面的皇后形成攻击
            ct=1;
            for(j=0;j<n;j++){
                if(WeiZhi[n]==WeiZhi[j]){    //形成攻击
                    ct=0;
                }else if(Math.abs(WeiZhi[j]-WeiZhi[n])==(n-j)){    //形成攻击
                    ct=0;
                }else{
                    
                }
            }
            if(ct==1)    //没有冲突，就开始下一列的试探
                eightQueen(n+1);    //递归调用
        }
    }
    
    public static void main(String[] args) {
        System.out.println("八皇后问题求解！");
        System.out.println("八皇后问题排列方案：");
        eightQueen(0);    //求解

    }

}

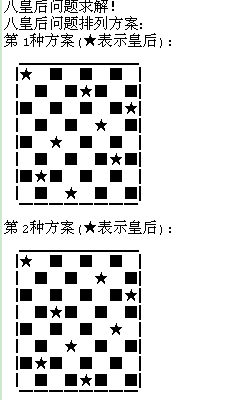
部分输出结果如下：