2.A star

2021-05-15 19:18:59

A*就不赘述，比较关键的地方需要注意。

下边内容参考自：

• 高飞--深蓝学院
• pathfinding.js
• https://www.redblobgames.com/

1.关于admisible

一个一定要明白的概念，就是admissible。

定义：h <= h*，则h就是admissible heuristic。其中h*到终点最小的真实cost。

只要h是admissible，那A*结果一定是最优的，否则就是次优的（换来的是计算速度提升）。

2.三种heuristic

先介绍代码中会用到的eigen中的几种范数，老是记不住：

• squaredNorm():  等价于vector自身点积，即所有元素平方和。
• norm(): 返回squaredNorm()的开方根，注意不管是几维的vector，都是开平方根。
• lpNorm< p >(): p取Infinity，就表示L∞范数，p取1就表示L1范数，p取2就表示L2范数

范数的概念：

• 1范数：即向量元素绝对值之和
• 2范数：Euclid范数（欧几里得范数，常用计算向量长度），即向量元素绝对值的平方和再开方
• ∞范数：即所有向量元素绝对值中的最大值

2.1 Euclidean Distance

double Astar::getEuclHeu(Eigen::Vector3d x1, Eigen::Vector3d x2)
{
  return tie_breaker_ * (x2 - x1).norm(); //norm = sqrt(squaredNorm())
}

理想结果是（PathFinding.js） VS 实际结果，正确！

        

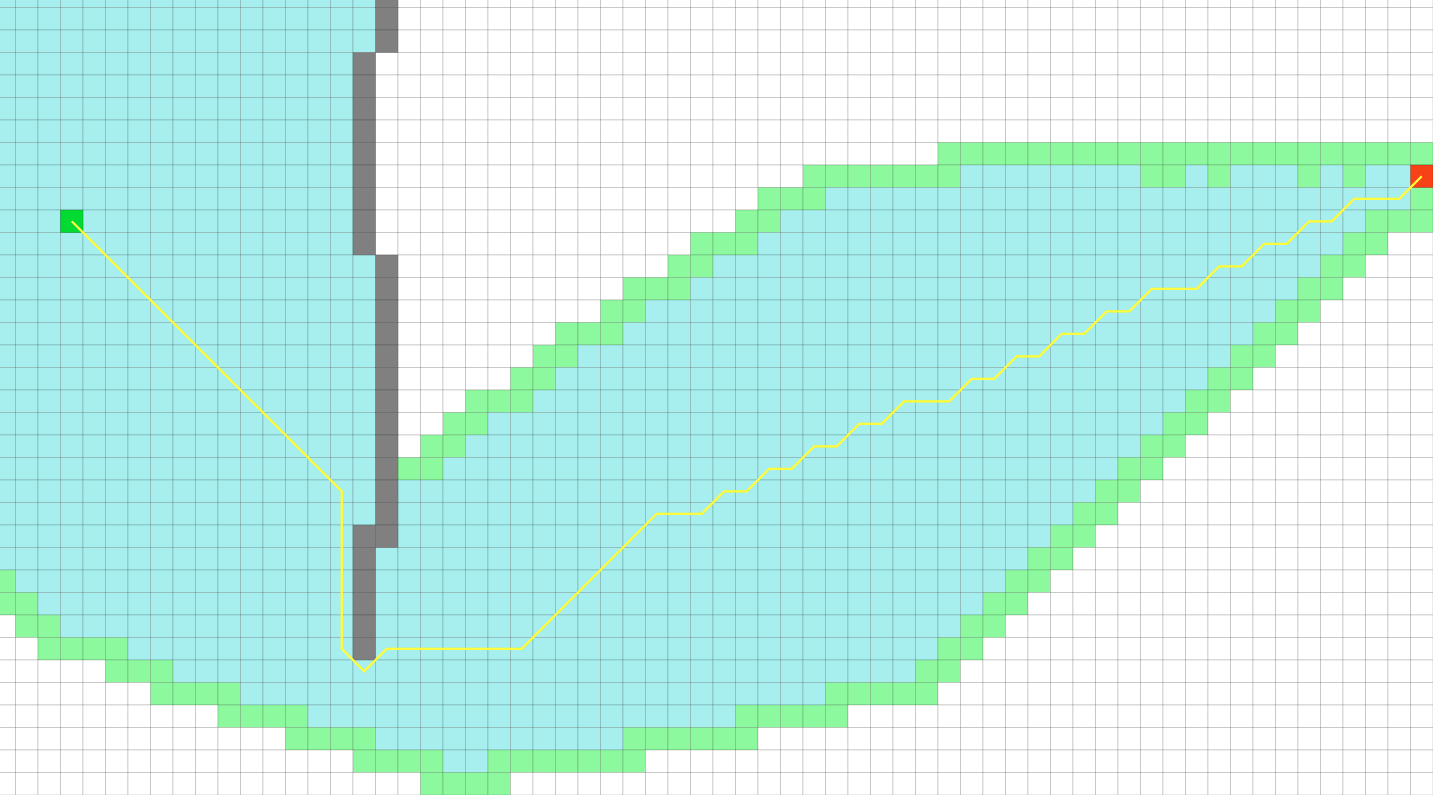
2.2 Manhattan Distance

引用：

在该网站的介绍中，有一个系数D，该如何理解。

文中定义D:两个相邻栅格之间的最小距离。

我的理解：这里之所以有D，是因为node是用的栅格索引，而不是物理上的位置，所以需要D，而我代码中，用的就是物理上的坐标，所以不需要D

function heuristic(node) =
    dx = abs(node.x - goal.x)
    dy = abs(node.y - goal.y)
    return D * (dx + dy)

double Astar::getManhHeu(Eigen::Vector3d x1, Eigen::Vector3d x2)
{
  double dx = fabs(x1(0) - x2(0));
  double dy = fabs(x1(1) - x2(1));return tie_breaker_ * (dx + dy);
}

理想结果是（PathFinding.js） VS 实际结果，正确！

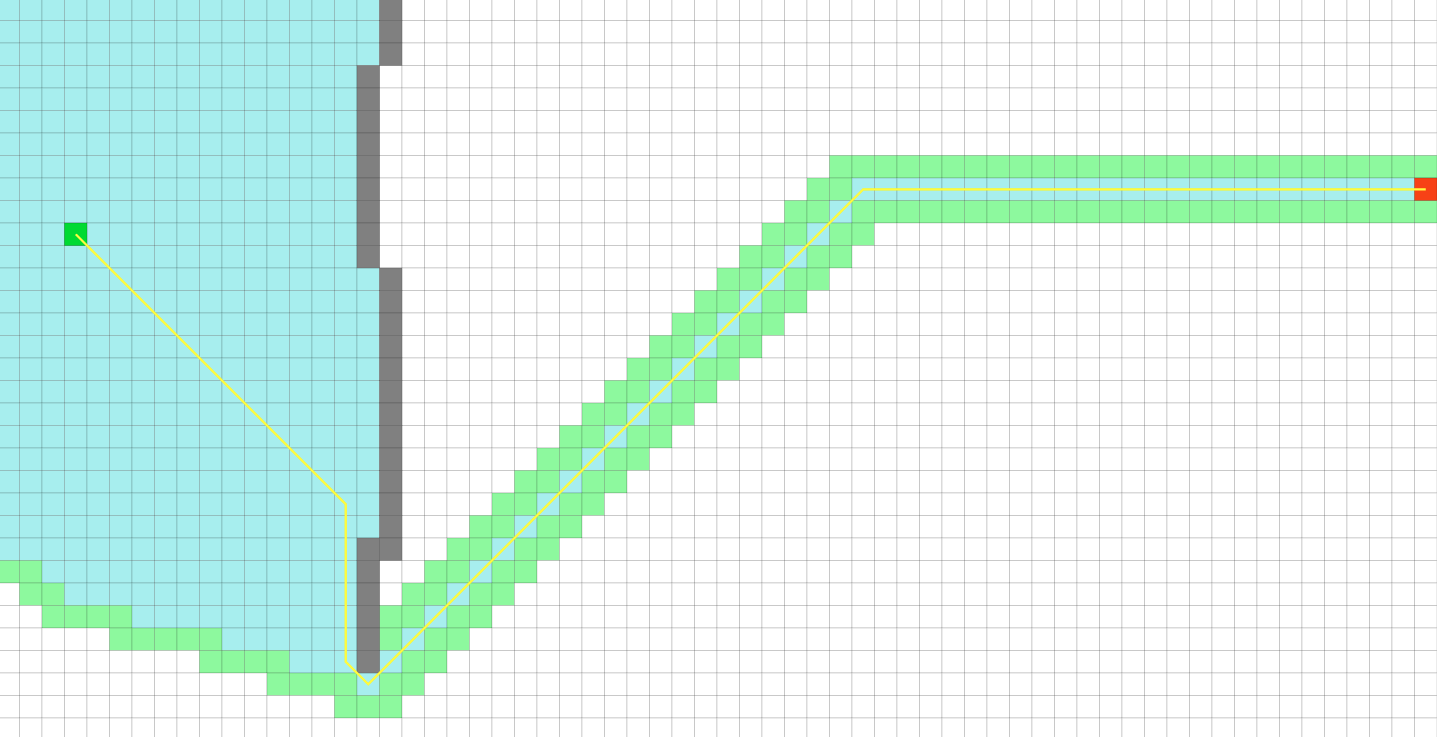
2.3 Diagonal Distance

引用：

如果曼哈顿需要上移4，右移4，共8*D，(D代表两个栅格的距离)

那Diagonal需要斜着移动4*D2。(D2代表一个栅格的对角线距离)

When D = 1 and D2 = 1, this is called the Chebyshev distance. When D = 1 and D2 = sqrt(2), this is called the octile distance.

我这里采用octile distance。

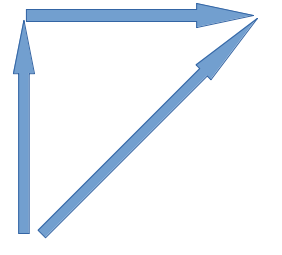
function heuristic(node) =
    dx = abs(node.x - goal.x)
    dy = abs(node.y - goal.y)
    return D * (dx + dy) + (D2 - 2 * D) * min(dx, dy)

代码里是不是有问题，没起作用呢？确实有问题，代码中对应sqrt(2)是D2，2是2*D，很明显我把栅格间距认为是1了，

但其实应该用自己的栅格地图的间距才行，我这里用的是0.05, 也就是说一个栅格的边长是0.05米。

double Astar::getDiagHeu(Eigen::Vector3d x1, Eigen::Vector3d x2)
{
  double dx = fabs(x1(0) - x2(0));
  double dy = fabs(x1(1) - x2(1));
  double h = (dx + dy) + 0.05 * (sqrt(2) - 2) * min(dx, dy);
  //double h = (dx + dy) + (sqrt(2) - 2) * min(dx, dy);
  return tie_breaker_ * h;
}

      理想结果是（PathFinding.js） VS 实际结果，正确！                                                         

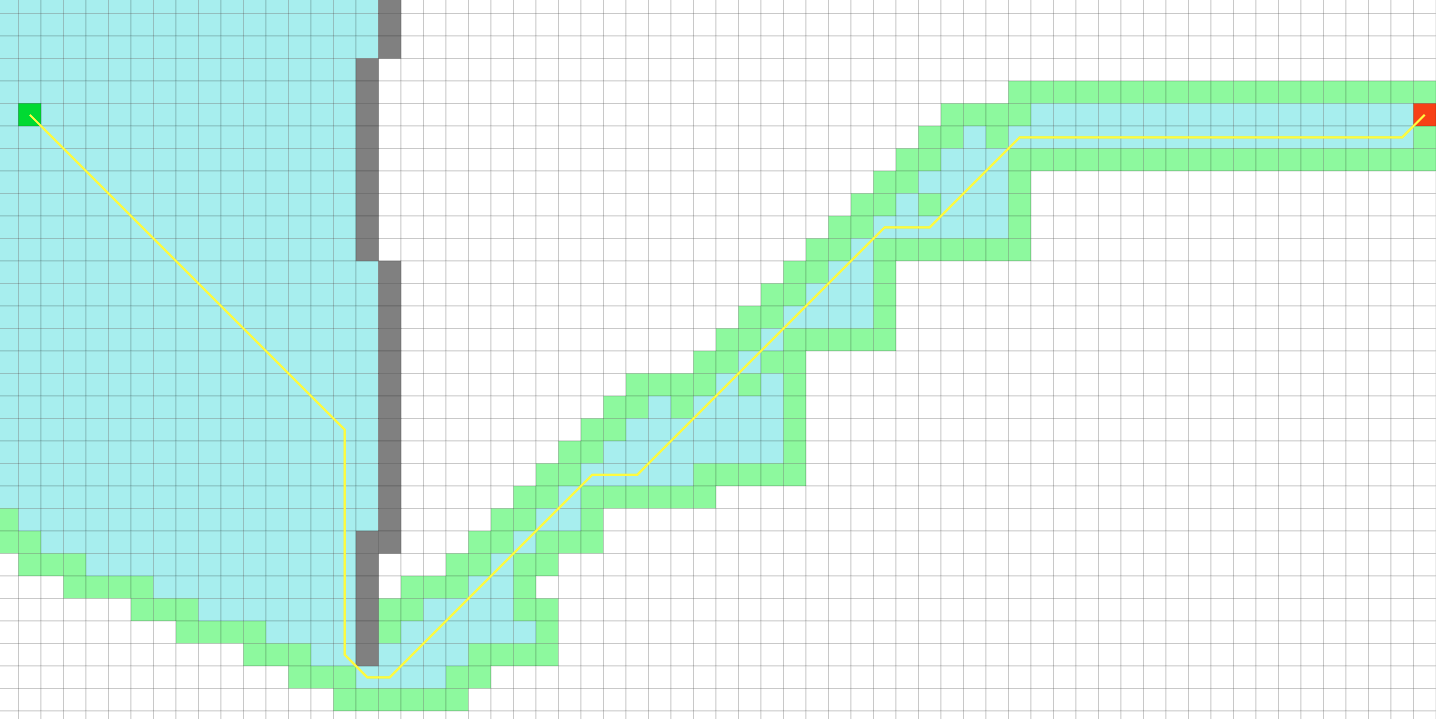
2.4 其他

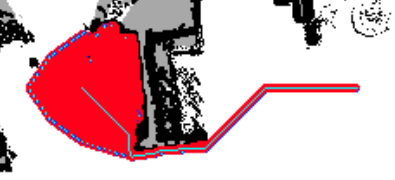
下边这个启发值，可以使得路径尽量保持起点到终点连接的直线，对于洗地车来说，是比较合适的，但是代码里哪里有问题，没起作用。

double Astar::getCrossHeu(Eigen::Vector3d s, Eigen::Vector3d c, Eigen::Vector3d e)
{
  double dx1 = (c(0) - e(0));
  double dy1 = (c(1) - e(1));
  double dx2 = (s(0) - e(0));
  double dy2 = (s(1) - e(1));
  double cross = fabs(dx1*dy2 - dx2*dy1);
  double h = (c-e).norm();
  h = h + cross*0.001;
  return h; //norm = sqrt(squaredNorm())
}

dx1 = current.x - goal.x
dy1 = current.y - goal.y
dx2 = start.x - goal.x
dy2 = start.y - goal.y
cross = abs(dx1*dy2 - dx2*dy1)
heuristic += cross*0.001
理想效果是这样的：

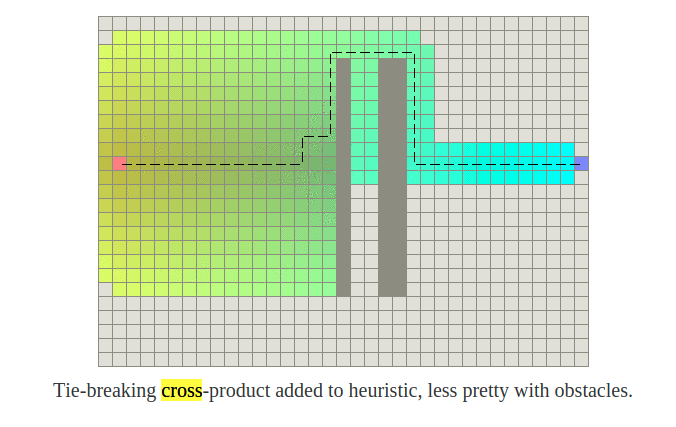
2.4 如何选用

引用http://theory.stanford.edu/~amitp/GameProgramming/Heuristics.html#heuristics-for-grid-maps中的内容：

　　四联通地图，用曼哈顿；

　　八联通地图，用对角线距离；

　　任意方向联通，用欧氏距离；

• On a square grid that allows 4 directions of movement, use Manhattan distance (L1).
• On a square grid that allows 8 directions of movement, use Diagonal distance (L∞).
• On a square grid that allows any direction of movement, you might or might not want Euclidean distance (L2). If A* is finding paths on the grid but you are allowing movement not on the grid, you may want to consider other representations of the map.
• On a hexagon grid that allows 6 directions of movement, use Manhattan distance adapted to hexagonal grids.

3.tie break

tie_break在代码里怎么不起作用呢？？

4. over-estimate heuristic

如果将a*用于lattice中计算启发值，那速度绝对要非常快才行，所以感觉次有解是很有必要的；

但是尝试过将h调大，有可能使得轨迹曲曲折折，这里应该需要cost function调整了。