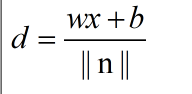点到空间中面的距离
有些时候我们在看计算机一些书籍的时候经常会涉及到空间中点与面之间的关系,书中会突然出现一些公式,可能很多时候我们会忘了证明的方法。
今天来谈谈点到空间中面的公式。
下面先给出空间中面的表示公式:
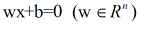
w是超平面的法向量,其维数不定。
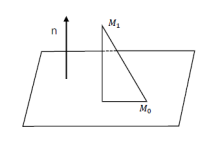
先假设我们有这样一个超平面,其法向量是n,现有一点M1,求M1到空间中面的距离。其实给出了这个图可能很多人已经想到了证明的方法,我们只要在平面上任取一个点顺水推舟就可以推导出来点到面的距离公式,可很多时候我们恰巧忽略了这个方法。
现在平面中任取一点M0,连接M0,M1,假设M01M1为一个向量。则M0M1在法向量n上的投影长度即为M1到超平面的距离。
且投影距离d为
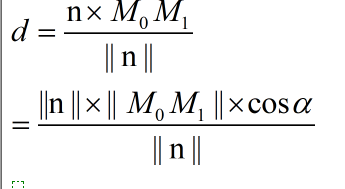
其中阿尔法即为M0M1与平面的夹角,有
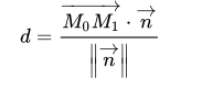
且知设OM0在空间中表示为向量为x0,OM1在空间中表示为向量为x,则M0M1=x-x0。且x0*w+b=0.
M0M1.n=(x-x0).n
则可得