python应用-scipy,numpy,sympy计算微积分

python应用-scipy,numpy,sympy计算微积分

今天来讲一下使用python进行微积分运算，python有很多科学计算库都可以进行微积分运算，当然如果知晓微积分计算的原理也可以自己编程实现。

下面我们用三种方式进行积分运算圆周率pi

numpy计算pi

import os
import numpy as np
#pi=4(1-1/3+1/5-1/7+1/9-.......)

n = 100000 
print(np.sum(4.0 / np.r_[1:n:4, -3:-n:-4]))
#3.141572693

讲解一下上面的代码
首先，这里的编程思路来源于一个公司，代码中也有注解

pi=4((1-1/3+1/5-1/7+1/9-1/11+1/13…)
这个公式怎么来的，实话说我也不知道
上面的代码思路就是，不可能说按照上面的公式计算无数项从1-1/3+1/5…到无穷项，所以我们就尽可能地去计算，去逼近真实结果，事实上，别的微积分计算函数也不能说就能计算无穷多项，其实也只是一种尽可能地逼近。上面的代码是取了1-1/3…1/99999。取到这个范围。
还要提到一个方法np.r_[]是指按行连接两个矩阵

所以如果我们呢自己去编程其实也是这样的一个思路

下面我给大家举一个很典型的例子。

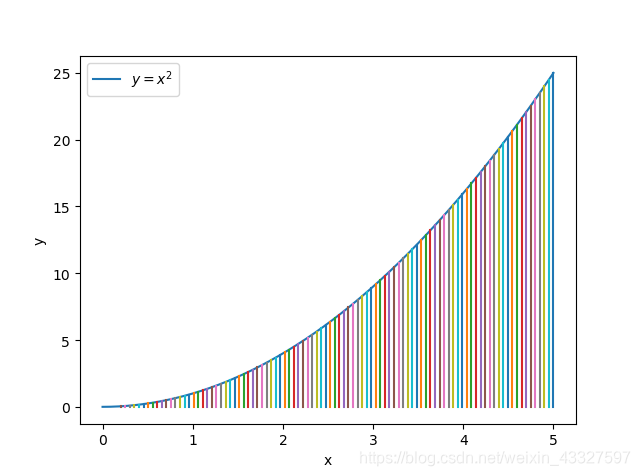
计算微函数$y=x^2$从0-5的积分，积分思路：将0-5的$y=x^2$图像进行切分，切成1000000个小矩形再求他们的面积和，说到这里很多人可能想起了高等数学教材上有关于这一节的积分知识。

下面给出代码：

import os
import numpy as np


#pi=4(1-1/3+1/5-1/7+1/9-.......)

n=1000000
print(sum((5/1000000)*(np.linspace(0,5,1000000)**2)))

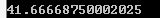
如果你用数学积分的知识计算，积分结果应该为125/3，上述结果的精确度已经达到0.00001了，下面给出图形并给出绘图代码方便大家形象化了解

x=np.linspace(0,5,1000)
y=x**2
plt.figure()
plt.xlabel('x')
plt.ylabel('y')
plt.plot(x,y,label="$y=x^2$")

plt.legend()
x=np.linspace(0,5,100)

for i in x:
    x_z=[]
    y_z=[]
    x_z.append(i)
    y_z.append(0) 
    x_z.append(i)
    y_z.append(i**2)
    plt.plot(x_z,y_z)

plt.show()

运行结果：

下面介绍的积分方法都是直接调用方法了

在下面的例子中，使用SciPy中提供的数值积分函数quad()计算π：

$pi=int_{-1}^1sqrt{1-x^2}dx$

scipy积分代码：

from scipy.integrate import quad 
print(quad(lambda x:(1-x**2)**0.5, -1, 1)[0] * 2 )
#3.141592653589797

如上面代码，quad，接受的第一个参数为一个函数，或者说一个积分公式，后面两个参数分别为积分下限和上限

下面用SymPy提供的符号积分函数integrate()对上面的公式进行积分运算，可以看到 运算的结果为符号表示的π：
代码：

from sympy import symbols, integrate, sqrt 
x = symbols("x") 
print(integrate(sqrt(1-x**2), (x, -1, 1)) * 2)

积分的方法为intergrate，我们需要先定义一个变量，然后传递参数，第一个参数为积分公式，第二个参数为积分上下限。