python panda数据分析操作
今天继续讲解一下pandas ,直接实战,用到了一个AMZN的csv数据文件,我把它上传到csdn资源平台,通过我的账号即可下载。
下面我们就来实战
首先我们需要读取文件
下面给出实例代码
path="C:/Users/Administrator/Desktop/o25mso/homework/AMZN.csv"
df=pd.read_csv(path)
上述代码path即为amzn文件的存储路径,如果你下载到不同的地方,路径需要改一下。这里就算是读取完成
我们给出输出结果
print(df.head())
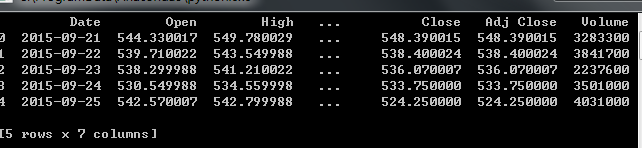
这里head()为dataframe的一个方法,输出对象的前五行。上面我们用的是read_csv函数读取的csv文件,通过这个方法得到的数据类型是一个DataFrame的数据类型,同样的pandas还有read_excel,read_josn这些类似的方法。
这里,还要提一下read_csv,几个常用的参数
header:传递一个数字,用于指定第几行为列名,默认为0也即是第一行。如果文件中没有列标题行这设置为none,用names参数传递一个列标题。
index_col跟header用法相似,也是传递一个数字,不过这里指定第几列作为行索引,有一个区别是,如果不传递参数,默认行索引为
range(len(df),也就是0,1,2,len(df)-1作为索引
engine:使用的分析引擎,有{‘c’, ‘python’}这两个分析引擎,c更快,而python更加完善,所以看需求选择。
nrows:需要读取的行数,如果文件特别大,这个函数作用就发挥出来了。传递一个整数。
names:用于结果的列名列表,如果数据文件中没有列标题行,就需要执行header=None。默认列表中不能出现重复,除非设定参数mangle_dupe_cols=True。
sep : str, default ‘,’指定分隔符。如果不指定参数,则会尝试使用逗号分隔。分隔符长于一个字符并且不是‘s+’,将使用python的语法分析器。并且忽略数据中的逗号。正则表达式例子:’ ’
好的基本上pandas读取文件上面的参数都是通用的,而且比较实用,所以可以耐心的看一看。
下面读取文件之后就做一些统计量分析
print(df.describe())
运行结果:
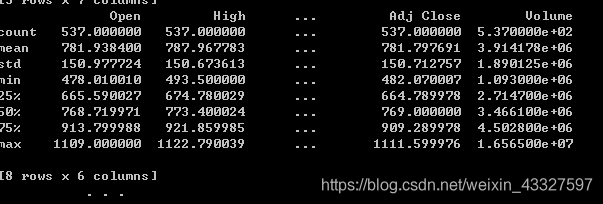
如上图,describe()这是一个基本信息统计函数,会得到一个DataFrame对象,统计信息包含统计对象每列的列数,均值,方差,最小值,最大值%25数值的数值%50数值。
这是一个可以帮助我们大致了解数据的函数。
下面我们调用一些统计方法,得到统计量
print(df.sum())
print(df.mean())
print(df.var())
print(df.std())
print(df.cov())
print(df.corr())
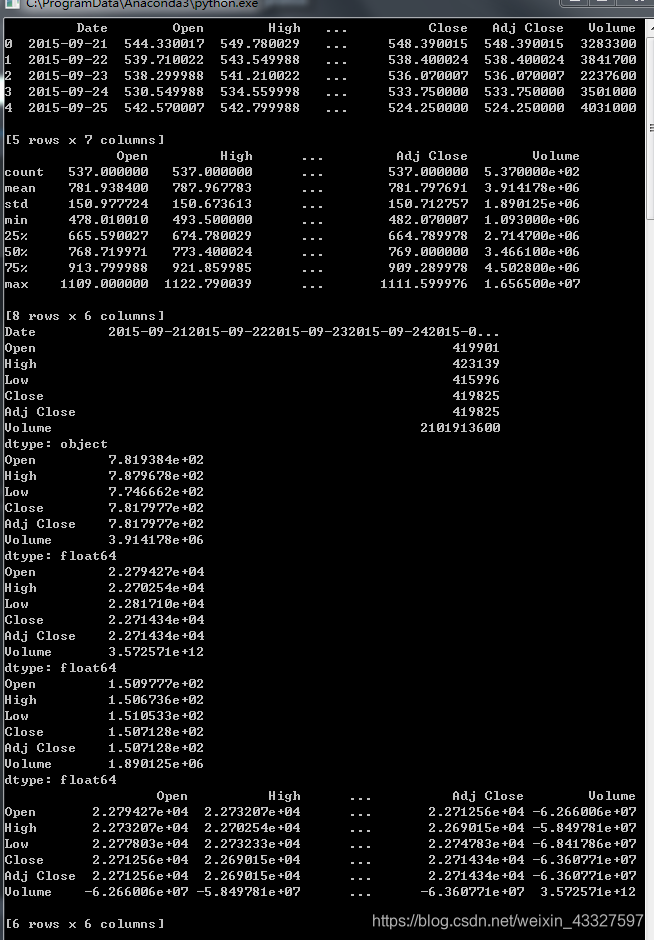
如上图的运行结果,这里需要说明一个注意点,默认pandas的方法都是针对列进行统计分析的,因为一个样本有很多属性,以一行的形式表现出来,如果按行统计,是无法统计的,且各属性相关系很小,没有按行统计的必要,所以一般按列统计,不过如果非要按行统计也可以,可以传递一个参数axis=1即可按照行进行统计。
现在解释一下上面几个方法的作用,上面的参数确实很有用,但是很多时候我们只是没有足够的应用场景,所以往往察觉不到他们的重要性。
sum()求和函数,默认得到每一列的数据的和,如果有一列数据为字符串,则将所有的字符串连接。做一个合并操作。
mean求均值,这个只对列的数据类型为数字性的有效。得到平均值
var()求方差
std()求标准差
corr()得到样本的相关系数矩阵,这里是person系数,这里的矩阵的得到是两两列进行计算。
cov()得到协方差矩阵,这个函数的操作过程和corr()差不多都是两两列进行求协方差,得到协方差矩阵。
上面的函数你如果对数据分析有过学习应该都知道,需要注意的是cov()和corr()这两个函数
如果两个变量的变化趋势一致,也就是说如果其中一个大于自身的期望值,另外一个也大于自身的期望值,那么两个变量之间的协方差就是正值。
如果两个变量的变化趋势相反,即其中一个大于自身的期望值,另外一个却小于自身的期望值,那么两个变量之间的协方差就是负值。
如果X与Y是统计独立的,那么二者之间的协方差就是0。
对于相关系数,系数越接近1说明两个变量越线性相关,如果越接近0两个变量关系越小为0时独立。
下面在介绍两个统计量,偏度和峰度
先介绍一下这两个变量:
偏度这一指标,又称偏斜系数、偏态系数,是用来帮助判断数据序列的分布规律性的指标。
在数据序列呈对称分布(正态分布)的状态下,其均值、中位数和众数重合。且在这三个数的两侧,其它所有的数据完全以对称的方式左右分布。
如果数据序列的分布不对称,则均值、中位数和众数必定分处不同的位置。这时,若以均值为参照点,则要么位于均值左侧的数据较多,称之为右偏;要么位于均值右侧的数据较多,称之为左偏;除此无它。
考虑到所有数据与均值之间的离差之和应为零这一约束,则当均值左侧数据较多的时候,均值的右侧必定存在数值较大的“离群”数据;同理,当均值右侧数据较多的时候,均值的左侧必定存在数值较小的“离群”数据。
一般将偏度定义为三阶中心矩与标准差的三次幂之比。
在上述定义下,偏度系数的取值无非三种情景:
1.当数据序列呈正态分布的时候,由于均值两侧的数据完全对称分布,其三阶中心矩必定为零,于是满足正态分布的数据序列的偏度系数必定等于零。
2.当数据序列非对称分布的时候,如果均值的左侧数据较多,则其右侧的“离群”数据对三阶中心矩的计算结果影响至巨,乃至于三阶中心矩取正值。因此,当数据的分布呈右偏的时候,其偏度系数将大于零。
3.当数据序列非对称分布的时候,如果均值的右侧数据较多,则其左侧的“离群”数据对三阶中心矩的计算结果影响至巨,乃至于三阶中心矩取负值。因此,当数据的分布呈左偏的时候,偏度系数将小于零。
在右偏的分布中,由于大部分数据都在均值的左侧,且均值的右侧存在“离群”数据,这就使得分布曲线的右侧出现一个长长的拖尾;而在左偏的分布中,由于大部分数据都在均值的右侧,且均值的左侧存在“离群”数据,从而造成分布曲线的左侧出现一个长长的拖尾。
可见,在偏度系数的绝对值较大的时候,最有可能的含义是“离群”数据离群的程度很高(很大或很小),亦即分布曲线某侧的拖尾很长。
但“拖尾很长”与“分布曲线很偏斜”不完全等价。例如,也不能排除在数据较少的那一侧,只是多数数据的离差相对于另一侧较大,但不存在明显“离群”数据的情景。所以,为准确判断分布函数的偏斜程度,最好的办法是直接观察分布曲线的几何图形。
与偏度(系数)一样,峰度(系数)也是一个用于评价数据系列分布特征的指标。根据这两个指标,我们可以判断数据系列的分布是否满足正态性,进而评价平均数指标的使用价值。一般地,对于一个偏态分布、肥尾分布特征很明显的数据序列来说,平均数这个指标极易令人误解数据序列分布的集中位置及其集中程度,故此使用起来要极其谨慎。
峰度(系数)等于数据序列的四阶中心矩与标准差的四次幂之比。设若先将数据标准化,则峰度(系数)相当于标准化数据序列的四阶中心矩。
显然,一个数据距离均值越远,其对四阶中心矩计算结果的影响越大。是故,峰度(系数)是一个用于衡量离群数据离群度的指标。峰度(系数)越大,说明该数据系列中的极端值越多。这在数据序列的分布曲线图中来看,体现为存在明显的“肥尾”。当然,峰度(系数)较大也可能说明离群数据取值的极端性很严重,或者各数据距离均值的距离普遍较远。可见,峰度(系数)的大小到底能说明什么问题,最好还是看图确定。
根据Jensen不等式,可以确定出峰度(系数)的取值范围:它的下限不会低于1,上限不会高于数据的个数。
有一些典型分布的峰度(系数)值得特别关注。例如,正态分布的峰度(系数)为常数3,均匀分布的峰度(系数)为常数1.6。在统计实践中,我们经常把这两个典型的分布曲线作为评价样本数据序列分布性态的参照。
在金融学中,峰度这个指标具有一定的意义。一项金融资产,设若其预期收益率的峰度较高,则说明该项资产的预期收益率有相对较高的概率取极端值。换句话说,该项资产未来行市发生剧烈波动的概率相对较高
代码如下
print(df.skew())
print(df.kurt())
运行结果如下:
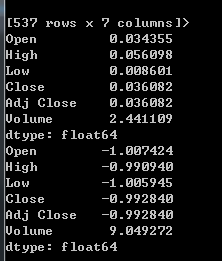
这里在介绍一下拓展统计函数
print(df.cumsum())
print(df.cummax())
print(df.iloc[:,1:].cumprod())
print(df.cummin())
这里结果就不展示了,运行结果太大
第三行代码可能发现有点不样,这里我解释一下,cumprod()是一个累乘函数,字符串不能相乘,所以排除掉,用iloc索引方法排除。
下面解释一下这些函数的作用
cumsum:按列累积求和
cummax:按列累积求最大值
cumprod:按列累计求乘积
cummin:按列累积求最小值
上面的函数求累积结果都是遍历整个列还有滚动计算
方法如下
df.iloc[:,1:].rolling(5).sum(),
df.iloc[:,1:].rolling(5).std(),
df.iloc[:,1:].rolling(5).var(),
df.iloc[:,1:].rolling(5).mean(),
df.iloc[:,1:].rolling(5).min(),
df.iloc[:,1:].rolling(5).max(),
df.iloc[:,1:].rolling(5).skew(),
df.iloc[:,1:].rolling(5).kurt(),
何为滚动?
这里的意思是形如df.rolling(5).sum()的代码意思是有一个长度为5的窗口挨个在数据之间滑动求每五个数据的和。可以一次类推其他函数。
下面。我在介绍一下一些基本绘图库:
plot()#折线图
pie()#饼图
hist()#二位条形直方图
boxplot()#绘制样本数据的箱型图
plot(logy=True)#绘制y轴的对数图形
plot(yerr=error)绘制误差条形图
下面一次给出简单实例:
plot
import matplotlib.pyplot as plt
plt.style.use("ggplot")
df.iloc[:,3].plot(label="first")
print(df)
df.iloc[:,2].plot(label="second")
plt.xlabel("time")
plt.ylabel("data")
plt.legend()
plt.show()
结果如图:
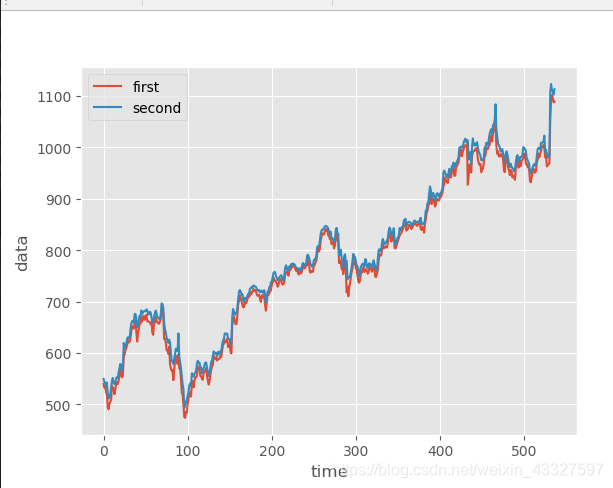
pie
size=[1000,300,211,122,120]
explode=[0,0.2,0,0,0]
plt.pie(size,explode=explode,autopct='%1.1f%%')
plt.show()
结果如图:
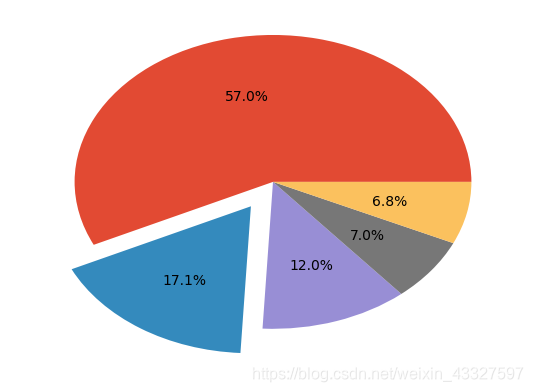
细节部分就不多做解释了。

df.iloc[:,1].hist(color='b',bins=12)
plt.show()
结果:
df.iloc[:,1:5].plot(kind='box')
plt.show()
结果:
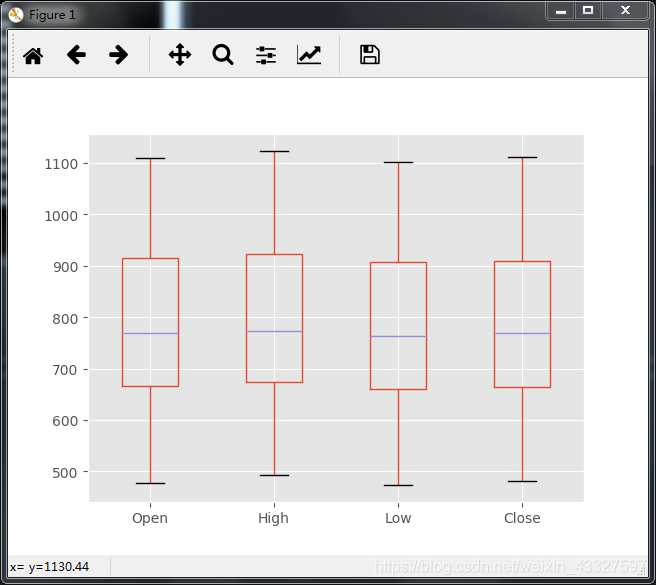
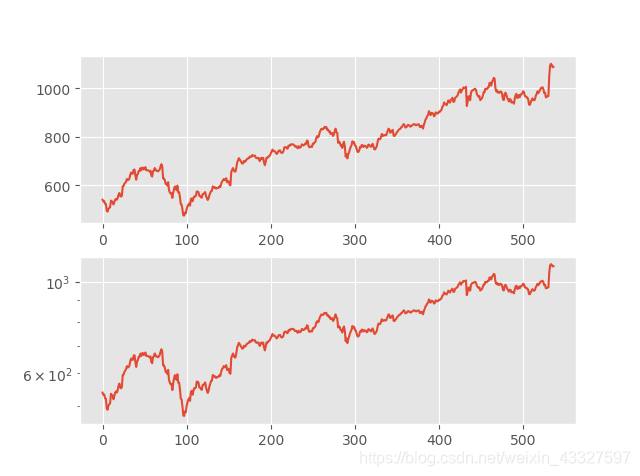
对数图
plt.subplot(211)
df.iloc[:,3].sort_index().plot(label='plot')
plt.subplot(212)
df.iloc[:,3].sort_index().plot(logy=True,label='log')
plt.show()
结果:
误差条形图
error=np.random.randn(len(df[0:20]))*10
df.iloc[:,3][0:20].plot(yerr=error)
plt.show()
结果: