第三讲 三维空间刚体运动
本讲目标
理解三维空间的刚体运动描述方式:旋转矩阵、变换矩阵、四元数和欧拉角。
掌握Eigen库的矩阵、几何模块使用方法。
3.1 点、向量和坐标系,旋转矩阵
二维空间与三维空间主要区别在于,其旋转性,二维空间有1个自由度,三维空间有三个自由度。

光说向量不一定跟几何数有关系,比如说三维空间中的向量会跟着三个数,这三个数是向量的坐标,向量坐标和向量本身并不是一回事儿,向量本身可以定义出加法或减法等运算,向量可以平移什么的。
向量的坐标是指向量在一个坐标系下面的一个表示:


外积:axb可以改成一个矩阵乘以矩阵b的形式,这个矩阵是一个反对称的矩阵,

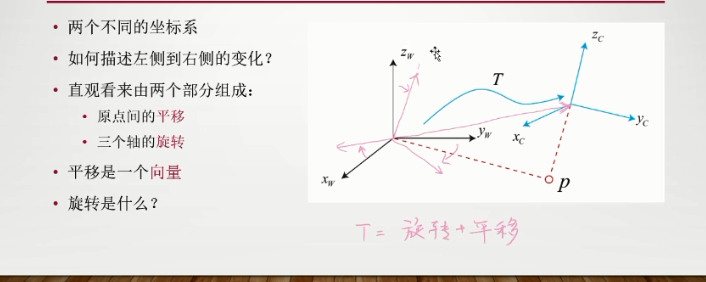
刚体运动:由平移和旋转组成

由于他们是同一个向量,故相等。

R就称为旋转矩阵,

当你有一个旋转矩阵的时候,也就定义出了一种运算,
a1=R12a2,指向量在2坐标系下的坐标a2经过旋转矩阵R12变成了1坐标系下的坐标a1.


光是旋转的话还是比较方便的,但是加上平移之后就会显得非常麻烦。
为了方便,把坐标向量都加上1,如下


比较偏向于世界坐标转机器人坐标,
旋转向量、欧拉角

三自由度的东西,用9个数来表示(3x3的旋转矩阵),有点浪费存储空间,用旋转矩阵来算的话还比较麻烦,而且还有一定约束,所以很困难,这就引入了其他的方式
任何一个旋转都可以用一个轴和一个角来表示,如上图的a旋转到b绕轴w,然后有一定角度。
称这种表示称为角轴或者旋转向量。
w描述了整个旋转,方向为一个长度为1的方向为n,角度的大小为Θ

由于旋转矩阵和角轴都不是很直观,下面引用欧拉角
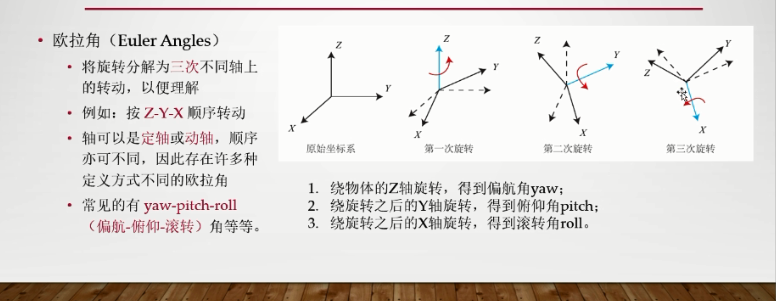
欧拉角不适用,它在计算中存在万向锁的事情,
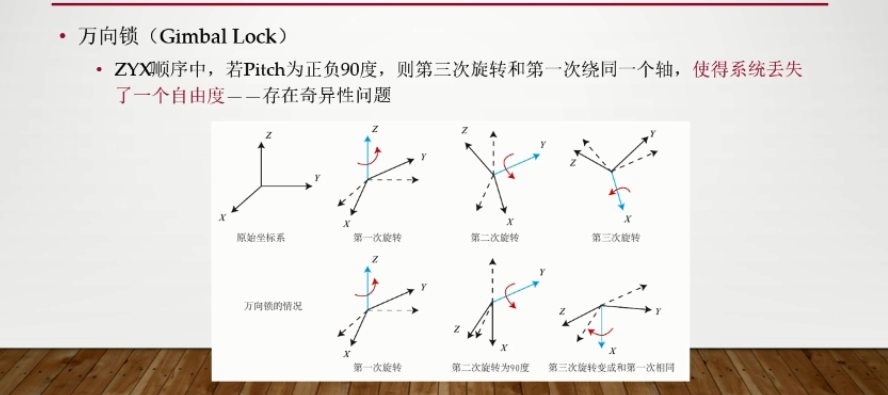
所以在工程中不太会使用欧拉角,而是在表达的时候使用欧拉角

四元素可以用来表达旋转的,在工程里面用处会更广泛一些

四元素可以表达成一个实部和3个虚部组成,


下面讲一下怎么用四元素去旋转一个空间点
将三维空间的点用虚的四元素来表示,
p'=qpq-1,先使用qp来旋转,把p旋转到四维空间,然后乘以一个q-1,把四维空间旋转到三维空间当中,

要把一个轨迹存储到一个文件里面的话,一般都是使用四元素,因为存一个矩阵很麻烦,要有九个量。

下面讲解一下EIGEN里面的几何模块
可视化演示
实践部分:EIGEN
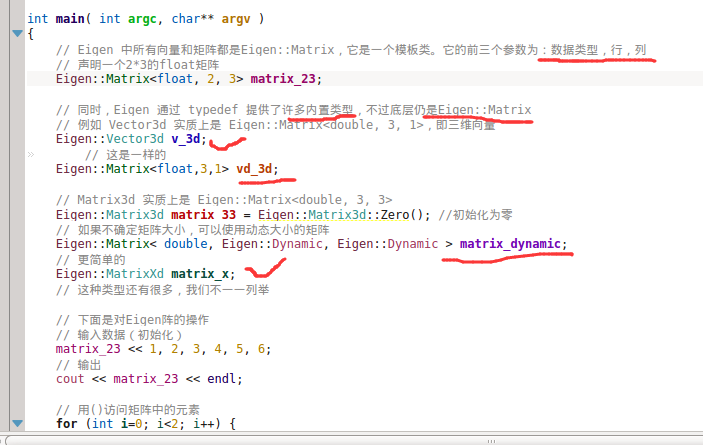
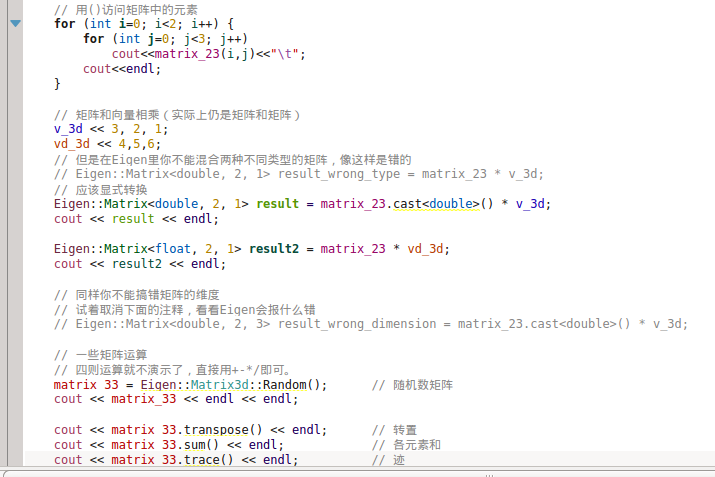
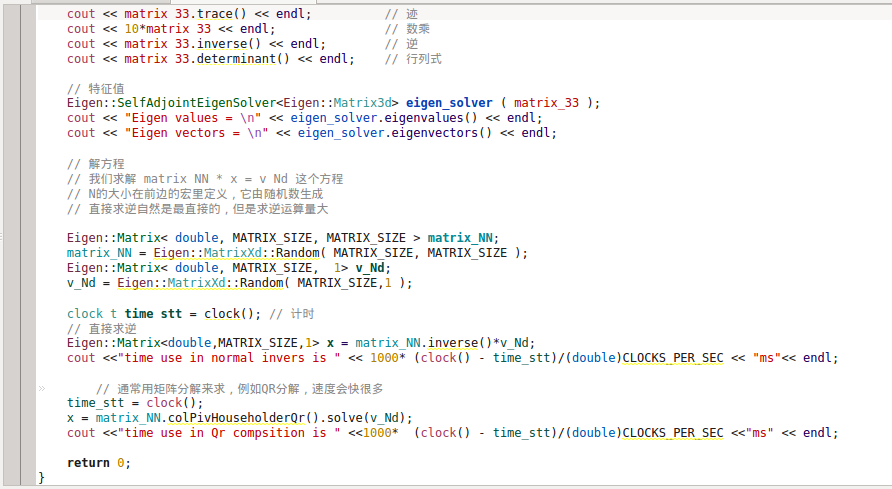
EIGEN它是在C++里面使用的一个矩阵库,效率高,优化做得好,在很多地方都用它去描述c++中的矩阵运算;
要事先安装EIGEN这个库,
sudo apt-get install libeigen3-dev
它会自动安装在目录/usr/include/eigen3/下面,在这里面就是EIGEN的头文件库,要引用这个头文件库,直接引用这里的文件就可以了
它是一个纯头文件的一个库,没有源文件,说明了在最后在使用的时候,不用链接什么库,直接在CMakeLists.txt里面加上头文件目录就可以了,如下
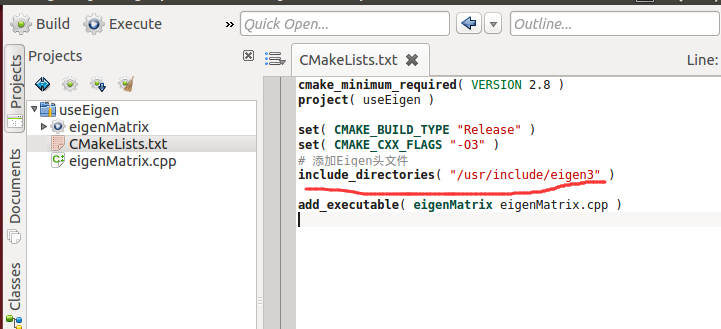
那么引进来之后就可以在源文件里面去加上eigen的头文件,
如Eigen/Core下有eigen的核心运算,
它跟matlab有点像,因为matlab所有的数据都是用矩阵来描述的,eigen也是使用矩阵来使用的;
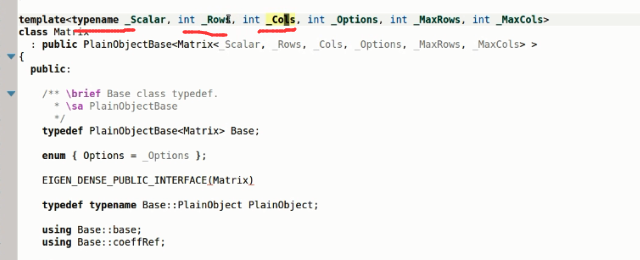
EIGEN的基本数据类型都是在Matrix里面的,他是一个模板类,它有6个模板参数,