// Eddy 继续
Problem Description
As is known, Ackermann function plays an important role in the sphere of theoretical computer science. However, in the other hand, the dramatic fast increasing pace of the function caused the value of Ackermann function hard to calcuate.
Ackermann function can be defined recursively as follows:
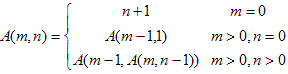
Now Eddy Gives you two numbers: m and n, your task is to compute the value of A(m,n) .This is so easy problem,If you slove this problem,you will receive a prize(Eddy will invite you to hdu restaurant to have supper).
Ackermann function can be defined recursively as follows:
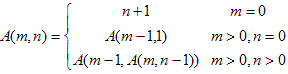
Now Eddy Gives you two numbers: m and n, your task is to compute the value of A(m,n) .This is so easy problem,If you slove this problem,you will receive a prize(Eddy will invite you to hdu restaurant to have supper).
Input
Each line of the input will have two integers, namely m, n, where 0 < m < =3.
Note that when m<3, n can be any integer less than 1000000, while m=3, the value of n is restricted within 24.
Input is terminated by end of file.
Note that when m<3, n can be any integer less than 1000000, while m=3, the value of n is restricted within 24.
Input is terminated by end of file.
Output
For each value of m,n, print out the value of A(m,n).
Sample Input
1 3 2 4
Sample Output
5 11
Author
eddy
/********************
看到哦这个题的第一眼感觉像是递推,然后依据那个题目中的公式发现不太好找。就先写了一个递归。打表,然后。恩。找规律……
打表,这才是真正的打表啊……
看到这个表,规律就不用我说了吧……
*************************/
Code:
#include <iostream>
#include <string.h>
#include <stdio.h>
using namespace std;
int num[30];
int main()
{
int i,j,n,m;
num[0] = 5;
for(i = 1;i<30;i++)
num[i] = num[i-1]*2+3;
while(cin>>m>>n&&m&&n)
{
if(m==1)
printf("%d
",n+2);
if(m==2)
printf("%d
",2*n+3);
if(m==3)
printf("%d
",num[n]);
}
return 0;
}
