codeforces Round #259(div2) D解决报告

D. Little Pony and Harmony Chest

time limit per test

4 seconds

memory limit per test

256 megabytes

input

standard input

output

standard output

Princess Twilight went to Celestia and Luna's old castle to research the chest from the Elements of Harmony.

A sequence of positive integers bi is harmony if and only if for every two elements of the sequence their greatest common divisor equals 1. According to an ancient book, the key of the chest is a harmony sequence bi which minimizes the following expression:

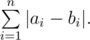
You are given sequence ai, help Princess Twilight to find the key.

Input

The first line contains an integer n (1 ≤ n ≤ 100) — the number of elements of the sequences a and b. The next line contains n integersa1, a2, ..., an (1 ≤ ai ≤ 30).

Output

Output the key — sequence bi that minimizes the sum described above. If there are multiple optimal sequences, you can output any of them.

Sample test(s)

input

5
1 1 1 1 1

output

1 1 1 1 1 

input

5
1 6 4 2 8

output

1 5 3 1 8 

题目大意：

给出N个数ai，求出还有一个序列bi。要求sum |ai-bi|，最短，且全部的bi都互质。

解法：

这里题目给了几个非常显眼的条件。ai限制在了1~30之间。因为能够bi无限选1这个数。那么|ai-bi| 最大就是29了，意味着bi < 59的。

要求全部的bi互质，能够化为全部的bi分解出来的质因数均不同样。bi < 59，有16个质数。这里我们非常easy联想到状态压缩DP了。

用s表示当前阶段用了哪些质因数的状态，比如 s = 3 = 11 代表眼下状态下使用了第一个和第二个质因数。

非常快我们就能够写出状态转移方程：

       f[i][s] = min(f[i-1][s^c[k]] + abs(a[i] - k))。    当中c[k]表示数字k使用了哪些质因数。

代码：

#include <cstdio>
#include <cmath>
#include <cstring>
#define M_max 60
#define N_max 123
#define inf 0x3f3f3f3f

using namespace std;

int p[N_max], c[M_max], a[N_max];
int f[N_max][1<<16], pre[N_max][1<<16][2];
int n, cnt, minnum, minpos;


void prime() {
	for (int i = 2; i <= M_max; i++) {
		bool flag = false;

		for (int j = 2; j <= sqrt(i); j++)
			if (i%j == 0) {
				flag = true;
				break;
			}

		if (!flag)  p[++cnt] = i;
	}

	for (int i = 1; i <= M_max; i++)
		for (int j = 1; j <= cnt; j++)
			if (i%p[j] == 0)
				c[i] |= 1 << (j-1);
}

void init() {
	prime();
	scanf("%d", &n);
	for (int i = 1; i <= n; i++)  scanf("%d", &a[i]);
}

void print(int x, int pos) {
	if (x == 0)  return;
	print(x-1, pre[x][pos][0]);
	printf("%d ", pre[x][pos][1]);
}

void solve() {
	memset(f, inf, sizeof(f));
	memset(f[0], 0, sizeof(f[0]));
	minnum = inf;

	for (int i = 1; i <= n; i++)
		for (int s = 0; s < (1<<16); s++)
			for (int k = 1; k <= M_max; k++)
				if ((s&c[k]) == c[k]) {
					int tmp = f[i-1][s^c[k]] + abs(a[i]-k);

					if (tmp < f[i][s]) {
						f[i][s] = tmp;
						pre[i][s][0] = s^c[k];
						pre[i][s][1] = k;
					}
				}
	for (int s = 0; s < (1<<16); s++)
		if (f[n][s] < minnum) {
			minnum = f[n][s];
			minpos = s;
		}

	print(n, minpos);
}

int main() {
	init();
	solve();
}

版权声明：本文博主原创文章，博客，未经同意不得转载。