见题:

很水的一题,数据范围太小,前缀和加爆搜就行.
#include<bits/stdc++.h> using namespace std; const int maxn=110; int ans=1,m,n,sum[maxn][maxn]; inline int read() { int x=0,ff=1; char ch=getchar(); while(!isdigit(ch)) { if(ch=='-') ff=-1; ch=getchar(); } while(isdigit(ch)) { x=(x<<1)+(x<<3)+(ch^48); ch=getchar(); } return x*ff; } inline void put(int x) { if(x<0) putchar('-'),x=-x; if(x>9) put(x/10); putchar(x%10+'0'); } int main() { //freopen("1.in","r",stdin); n=read();m=read(); for(int i=1;i<=n;i++) { for(int j=1;j<=m;j++) { int x=read(); sum[i][j]=sum[i-1][j]+sum[i][j-1]-sum[i-1][j-1]+x; } } for(int len=2;len<=min(n,m);len++) { int he=len*len; for(int x1=1;x1<=n-len+1;x1++) { for(int y1=1;y1<=m-len+1;y1++) { int x2=x1+len-1; int y2=y1+len-1; if((sum[x2][y2]-sum[x1-1][y2]-sum[x2][y1-1]+sum[x1-1][y1-1])==he) ans=len; } } } put(ans); return 0; }
可是还是想写正解,DP;
对于这类的二维DP,个人理解就是如果保存的从起点到终点的状态会被一些情况所中断,就要只考虑最下角的点所保存的点的状态,例如此题,我们可以保存以(i,j)为右下角的状态,以f[i][j]保存以(i,j)为最右下角的最大正方形边长.状态转移怎么样呢?
这是我们我们可以轻易的想起二维的前缀和:f[i][j]=f[i-1][j]+f[i][j-1]-f[i-1][j-1]+a[i][j],那这个能否用前缀和处理呢,见下图:

最右下的小矩阵代表(i,j)可以很清楚地看出由左边的点,上边的点,左上角的点三个点的最小矩阵构成以个完整的矩阵,即:if(a[i][j]==1) f[i][j]=min(f[i-1][j-1],min(f[i-1][j],f[i][j-1]))+1;
这也提醒我们min的意义就是几个状态都具备的共同元素.
#include<bits/stdc++.h> using namespace std; const int maxn=110; int m,n,a[maxn][maxn],f[maxn][maxn],ans; inline int read() { int x=0,ff=1; char ch=getchar(); while(!isdigit(ch)) { if(ch=='-') ff=-1; ch=getchar(); } while(isdigit(ch)) { x=(x<<1)+(x<<3)+(ch^48); ch=getchar(); } return x*ff; } int put(int x) { if(x<0) putchar('-'),x=-x; if(x>9) put(x/10); putchar(x%10+'0'); } inline void DP() { for(int i=1;i<=n;i++) { for(int j=1;j<=m;j++) { if(a[i][j]==1) f[i][j]=min(f[i-1][j-1],min(f[i-1][j],f[i][j-1]))+1; ans=max(ans,f[i][j]); } } } int main() { freopen("1.in","r",stdin); n=read();m=read(); for(int i=1;i<=n;i++) { for(int j=1;j<=m;j++) a[i][j]=read(); } DP(); put(ans); return 0; }
下一题:

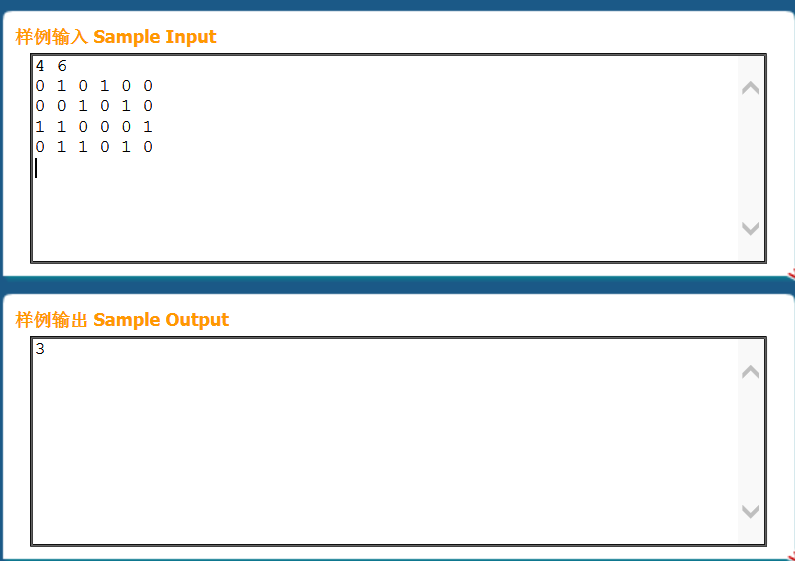
这一题就不能用暴力了,(n<=2600,m<=2600)只能想正解,和上一题一样我们可以用f[i][j]一(i,j)保存合法的吃到的最大的鱼的个数.
接下来就考虑状态怎么转移,我自己也是嗑了许多时间还没做出来,于是就看了题解...

给出代码:
#include<bits/stdc++.h> using namespace std; #define _ 0 const int maxn=2600; int m,n,a[maxn][maxn],f[maxn][maxn],s1[maxn][maxn],s2[maxn][maxn],ans; inline int read() { int x=0,ff=1; char ch=getchar(); while(!isdigit(ch)) { if(ch=='-') ff=-1; ch=getchar(); } while(isdigit(ch)) { x=(x<<1)+(x<<3)+(ch^48); ch=getchar(); } return x*ff; } inline void put(int x) { if(x<0) putchar('-'),x=-x; if(x>9) put(x/10); putchar(x%10+'0'); } int main() { freopen("1.in","r",stdin); n=read();m=read(); for(int i=1;i<=n;i++) { for(int j=1;j<=m;j++) a[i][j]=read(); } for(int i=1;i<=n;i++) { for(int j=1;j<=m;j++) { if(!a[i][j]) { s1[i][j]=s1[i][j-1]+1; s2[i][j]=s2[i-1][j]+1; } if(a[i][j]) { f[i][j]=min(f[i-1][j-1],min(s1[i][j-1],s2[i-1][j]))+1; ans=max(ans,f[i][j]); } } } memset(f,0,sizeof(f)); memset(s1,0,sizeof(s1)); memset(s2,0,sizeof(s2)); for(int i=1;i<=n;i++) { for(int j=m;j>=1;j--) { if(!a[i][j]) { s1[i][j]=s1[i][j+1]+1; s2[i][j]=s2[i-1][j]+1; } if(a[i][j]) { f[i][j]=min(f[i-1][j+1],min(s1[i][j+1],s2[i-1][j]))+1; ans=max(ans,f[i][j]); } } } put(ans); return (0^_^0); }
启示我们可以直接从最优解的转移推状态转移方程...