最大有效子矩阵

安利一个好的博客

定义：

有效子矩阵：符合条件的子矩阵。

最大有效子矩阵：给定的矩阵中最大的有效子矩阵。

题目就是求最大有效子矩阵有多大？

能用DP写的前提是：最大有效子矩阵中每一个每一个矩阵都为有效矩阵.

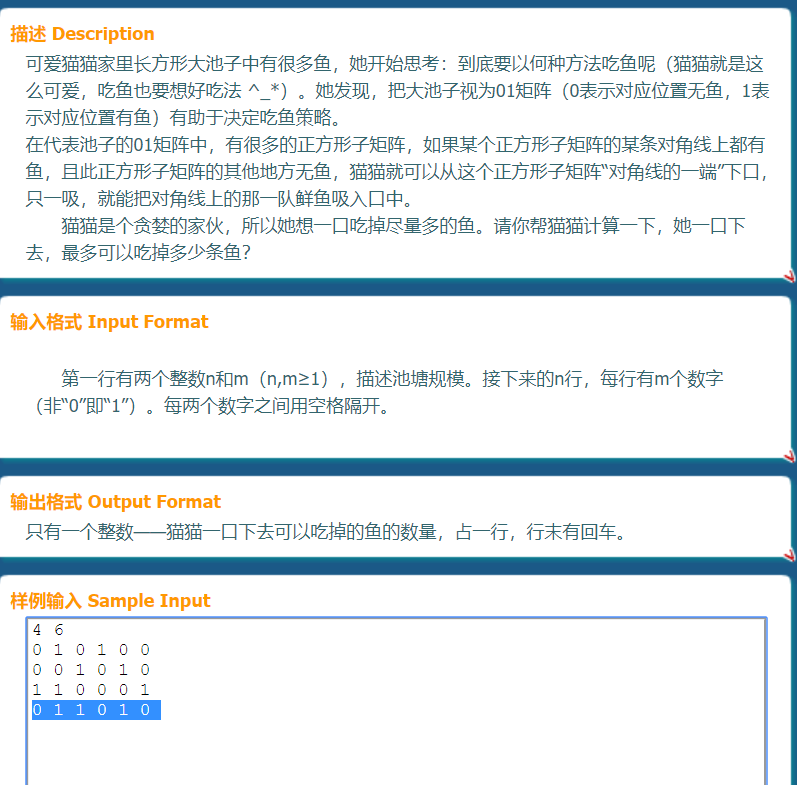
见题：

题目显然求的是最大的有效子矩阵（正方形看做特殊的矩阵）。

这里就要讲到一个牛逼的方法，割线法。（我也是今天才学的）.

记得以前学过确定最大有效正方形的大小的题，是用f[i][j]表示以点(i,j)最多向左和向右延展多长是有效的正方形。

状态转移：if（...）f[i][j]=min（f[i-1][j],min(f[i-1][j-1],f[j][i-1])）+1;

正方形用一个数组即表示信息，因为边长都相等.

但长方形就不行了，需要用三个数组，left[i][j],right[i][j],up[i][j];

分别表示以点（i，j）向左，向右，向上最大延展的长度.

先上代码：

#include<bits/stdc++.h>
const int maxn=2100;
using namespace std;
int n,m,ans1,ans2;
int l[maxn][maxn],r[maxn][maxn],u[maxn][maxn],a[maxn][maxn];
int main()
{
    freopen("1.in","r",stdin);
    cin>>n>>m;
    for(int i=1;i<=n;i++)
        for(int j=1;j<=m;j++) 
        {
            cin>>a[i][j];
            u[i][j]=l[i][j]=r[i][j]=1;//初始化每个点都不能延展，即长度都为1.
        }
    for(int i=1;i<=n;i++)
        for(int j=1;j<=m;j++)
        {
            if(j==1) continue;
            if(a[i][j]!=a[i][j-1]) l[i][j]+=l[i][j-1];//预处理l数组，
        }
    for(int i=1;i<=n;i++)
        for(int j=m;j>=1;j--)
        {
            if(j==m) continue;
            if(a[i][j]!=a[i][j+1]) r[i][j]+=r[i][j+1];//预处理r数组.
        }
    for(int i=1;i<=n;i++)
        for(int j=1;j<=m;j++)
        {
            if(i!=1&&a[i][j]!=a[i-1][j])
            {
                l[i][j]=min(l[i][j],l[i-1][j]);
                r[i][j]=min(r[i][j],r[i-1][j]);
                u[i][j]=u[i-1][j]+1;
            }
            int a=l[i][j]+r[i][j]-1;
            int b=u[i][j];
            ans1=max(min(a,b)*min(a,b),ans1);
            ans2=max(ans2,a*b);
        }    
    cout<<ans1<<endl<<ans2<<endl;
    return 0;
}

经过前两个预处理，每个点的l与r数组相加就会有一个长度，而一条枞线上的点就变成了长度不一的线段，那经过这条线的最大矩阵就是线的长度与最短长度的相乘.

我们可以看到在第三个f循坏里，还要更新l和r的信息，我们可以跟着走一遍会发现，这个循环的作用是寻找最短的长度，而抛弃原有的信息，我们可以发现l和r只随i的更新而更新.即随着i的更新，l和r不断寻找最短长度，而与左右的点得l和r的值无关.

 之后以此处理每个矩阵即可。

2：

#include<bits/stdc++.h>
const int maxn=1100;
using namespace std;
int n,m,l[maxn][maxn],r[maxn][maxn],u[maxn][maxn],ans;
char ch[maxn][maxn];
int main()
{
    freopen("1.in","r",stdin);
    cin>>n>>m;
    for(int i=1;i<=n;i++)
        for(int j=1;j<=m;j++) 
        {
            cin>>ch[i][j];
            if(ch[i][j]=='F') l[i][j]=r[i][j]=u[i][j]=1;
        }
    for(int i=1;i<=n;i++)
        for(int j=1;j<=m;j++)
        {
            if(j==1) continue;
            if(ch[i][j]=='F') l[i][j]=l[i][j-1]+1;
        }
    for(int i=1;i<=n;i++)
        for(int j=m;j>=1;j--)
        {
            if(j==m) continue;
            if(ch[i][j]=='F') r[i][j]=r[i][j+1]+1;
        }
    for(int i=1;i<=n;i++)
        for(int j=1;j<=m;j++)
        {
            if(ch[i][j]=='R') continue;
            if(i!=1&&ch[i-1][j]=='F')
            {
                l[i][j]=min(l[i][j],l[i-1][j]);
                r[i][j]=min(r[i][j],r[i-1][j]);
                u[i][j]=u[i-1][j]+1;
            }
            int a=l[i][j]+r[i][j]-1;
            int b=u[i][j];
            ans=max(ans,a*b);
        }
        cout<<ans*3<<endl;
        return 0;
} 

下一题：

#include<bits/stdc++.h>
using namespace std;
#define _ 0
const int maxn=2600;
int m,n,a[maxn][maxn],f[maxn][maxn],s1[maxn][maxn],s2[maxn][maxn],ans;
inline int read()
{
    int x=0,ff=1;
    char ch=getchar();
    while(!isdigit(ch))
    {
        if(ch=='-') ff=-1;
        ch=getchar();
    }
    while(isdigit(ch))
    {
        x=(x<<1)+(x<<3)+(ch^48);
        ch=getchar();
    }
    return x*ff;
}
inline void put(int x)
{
    if(x<0) putchar('-'),x=-x;
    if(x>9) put(x/10);
    putchar(x%10+'0');
}
int main()
{
    //freopen("1.in","r",stdin);
    n=read();m=read();
    for(int i=1;i<=n;i++)
    {
        for(int j=1;j<=m;j++) a[i][j]=read();        
    }
    for(int i=1;i<=n;i++)
    {
        for(int j=1;j<=m;j++) 
        {
            if(!a[i][j]) 
            {
                s1[i][j]=s1[i][j-1]+1;
                s2[i][j]=s2[i-1][j]+1;
            }
            if(a[i][j])
            {
                f[i][j]=min(f[i-1][j-1],min(s1[i][j-1],s2[i-1][j]))+1;
                ans=max(ans,f[i][j]);
            }
        }
    }
    memset(f,0,sizeof(f));
    memset(s1,0,sizeof(s1));
    memset(s2,0,sizeof(s2));
    for(int i=1;i<=n;i++)
    {
        for(int j=m;j>=1;j--)
        {
            if(!a[i][j]) 
            {
                s1[i][j]=s1[i][j+1]+1;
                s2[i][j]=s2[i-1][j]+1;
            }
            if(a[i][j])
            {
                f[i][j]=min(f[i-1][j+1],min(s1[i][j+1],s2[i-1][j]))+1;
                ans=max(ans,f[i][j]);
            }
        }
    }
    put(ans);
    return (0^_^0);
}

具体情况具体分析，主要看题目要求的目标矩阵满足的条件设置变量.