假设询问的是((x,y),x>y)。
考虑建一棵树,每个点代表一个二元组((a,b)(a>b,a le m))。如果((a,b))进行一次操作后会变成((a',b')),那么((a',b'))是((a,b))的父节点。要求的就是((x,y))的子树大小( imes 2)。
容易发现((a,b))的直接儿子是((a+b,a),(2a+b,a),(3a+b,a)dots)。如下图:
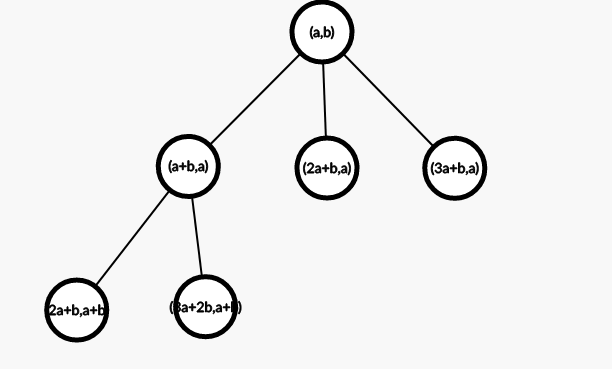
考虑改变连边方式,变成这样:
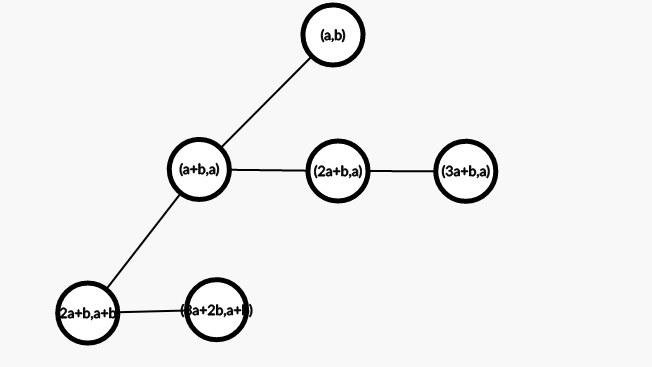
再将奇数层(假设((a,b))在第0层)的点编号两维取反,变成这样:
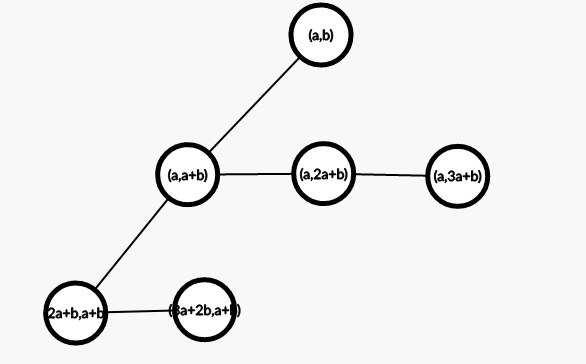
问题变成了,一开始有一个二元组((x,x+y)),每次可以进行以下两种操作之一:
((a,b)->(a+b,b))
((a,b)->(a,a+b))
问能到达多少节点。
用二元组((p,q))表示一个数(px+q(x+y)),那么就是一开始有一个四元组(((1,0),(0,1))),每次可以进行以下两种操作之一:
(((a,b),(c,d))->((a+c,b+d),(b,d)))
(((a,b),(c,d))->((a,b),(a+c,b+d)))
可以发现这类似于Stern-Brocot Tree的构造过程,在不考虑(le m)限制的前提下,SBTree上任意两个相邻节点代表一个合法的四元组。如下图:
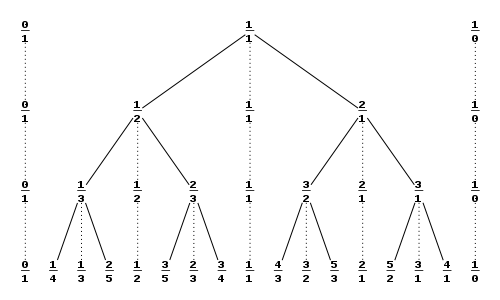
现在有了(le m)的限制,一对合法四元组是由两个二元组组成的,考虑在较大的那个二元组处统计它。(较大的二元组指两维都较大的二元组,这里因为题目性质,两维都较大的说法是不存在歧义的。)根据SBTree的性质,一对二元组((i,j))出现过当且仅当(gcd(i,j)=1),且每个二元组会作为较大值贡献答案(2)次(如上图,在且仅在该二元组第一次出现的那一层,它比相邻两个二元组大)。(le m)的限制就是额外要求(xi+(x+y)j le m)。
那么要求的子树大小就是(2 imes sum_{i,j}[gcd(i,j)=1][xi+(x+y)j le m])。随便莫比乌斯反演以后杜教筛+类欧搞搞就完事了!!1
#include<bits/stdc++.h>
using namespace std;
const int N=2e6+10;
typedef long long ll;
int gi() {
int x=0,o=1;char ch=getchar();
while((ch<'0'||ch>'9')&&ch!='-') ch=getchar();
if(ch=='-') o=-1,ch=getchar();
while(ch>='0'&&ch<='9') x=x*10+ch-'0',ch=getchar();
return x*o;
}
int mu[N],smu[N],m;
map<int,int> M;
ll ans;
int getsmu(int n) {
if(n<N) return smu[n];
if(M.count(n)) return M[n];
int ret=1;
for(int i=2,j;i<=n;i=j+1) {
j=n/(n/i);ret-=(j-i+1)*getsmu(n/i);
}
return M[n]=ret;
}
ll cal(ll n,ll a,ll b,ll c) {
if(n<0) return 0;
if(!a) return (b/c)*(n+1);
if(a>=c||b>=c) return cal(n,a%c,b%c,c)+n*(n+1)/2*(a/c)+(n+1)*(b/c);
ll m=(a*n+b)/c;
return n*m-cal(m-1,c,c-b-1,a);
}
ll cal(int x,int y,int n) {
return cal(n/x-1,x,n%x,y);
}
int main() {
mu[1]=1;
for(int i=1;i<N;i++)
for(int j=i+i;j<N;j+=i) mu[j]-=mu[i];
for(int i=1;i<N;i++) smu[i]=smu[i-1]+mu[i];
int T=gi();m=gi();
while(T--) {
int x=gi(),y=gi();
if(x>m||y>m) cout<<"0
";
else if(x<=y) cout<<"1
";
else {
y+=x;
if(y>m) cout<<"2
";
else {
ans=4;
for(int i=1,j;i<=m;i=j+1) {
j=m/(m/i);ans+=4ll*(getsmu(j)-getsmu(i-1))*cal(x,y,m/i);
}
cout<<ans<<'
';
}
}
}
return 0;
}