来源:https://www.zhihu.com/question/26408259
问题分析
我们可以通过强化学习(reinforcement learning)来解决小鸟怎么飞这个问题。强化学习中有状态(state)、动作(action)、奖赏(reward)这三个要素。智能体(Agent,指小鸟)会根据当前状态来采取动作,并记录被反馈的奖赏,以便下次再到相同状态时能采取更优的动作。
状态的选择
在这个问题中,最直观的状态提取方法就是以游戏每一帧的画面为状态。但为了简化问题,这里我将选用SarvagyaVaish项目中提出的状态表达:取小鸟到下一组管子的水平距离和垂直距离差作为小鸟的状态。更准确地说, 与
的定义如下图所示:
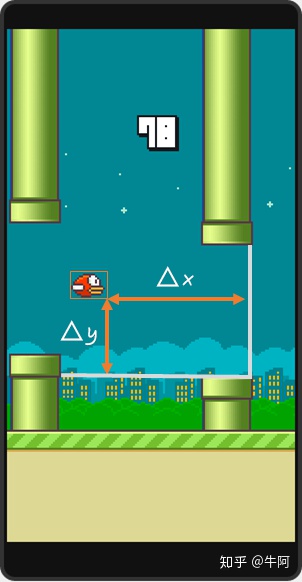
对于每一个状态,
为水平距离,
为垂直距离。
动作的选择
每一帧,小鸟只有两种动作可选:1.向上飞一下。2.什么都不做。
奖赏的选择
小鸟活着时,每一帧给予1的奖赏;若死亡,则给予-1000的奖赏。
关于Q
提到Q-learning,我们需要先了解Q的含义。
Q为动作效用函数(action-utility function),用于评价在特定状态下采取某个动作的优劣。它是智能体的记忆。
在这个问题中, 状态和动作的组合是有限的。所以我们可以把Q当做是一张表格。表中的每一行记录了状态,选择不同动作(飞或不飞)时的奖赏:
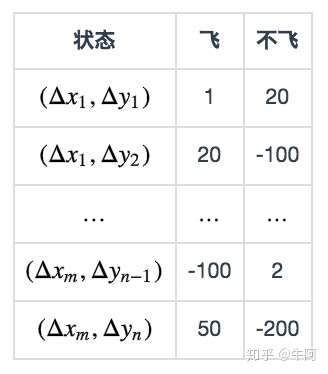
这张表一共 行,表示
个状态,每个状态所对应的动作都有一个效用值。
理想状态下,在完成训练后,我们会获得一张完美的Q表格。我们希望只要小鸟根据当前位置查找到对应的行,选择效用值较大的动作作为当前帧的动作,就可以无限地存活。
训练
下面的伪代码说明了我们如何训练,来得到一个尽量完美的Q表格。
初始化 Q = {};
while Q 未收敛:
初始化小鸟的位置S,开始新一轮游戏
while S != 死亡状态:
使用策略π,获得动作a=π(S)
使用动作a进行游戏,获得小鸟的新位置S',与奖励R(S,a)
Q[S,A] ← (1-α)*Q[S,A] + α*(R(S,a) + γ* max Q[S',a]) // 更新Q
S ← S'其中有些值得注意的地方:
1. 使用策略π,获得动作a=π(S)
最直观易懂的策略π(S)是根据Q表格来选择效用最大的动作(若两个动作效用值一样,如初始时某位置处效用值都为0,那就选第一个动作)。
但这样的选择可能会使Q陷入局部最优:在位置 处,在第一次选择了动作1(飞)并获取了
的奖赏后,算法将永远无法对动作2(不飞)进行更新,即使动作2最终会给出
的奖赏。
改进的策略为ε-greedy方法:每个状态以ε的概率进行探索,此时将随机选取飞或不飞,而剩下的1-ε的概率则进行开发,即按上述方法,选取当前状态下效用值较大的动作。
2.更新Q表格
Q表格将根据以下公式进行更新:
其中α为学习速率(learning rate),γ为折扣因子(discount factor)。根据公式可以看出,学习速率α越大,保留之前训练的效果就越少。折扣因子γ越大,所起到的作用就越大。但
指什么呢?
考虑小鸟在对状态进行更新时,会关心到眼前利益( ),和记忆中的利益(
)。
是记忆中的利益。它是小鸟记忆里,新位置
能给出的最大效用值。如果小鸟在过去的游戏中于位置
的某个动作上吃过甜头(例如选择了某个动作之后获得了50的奖赏),这个公式就可以让它提早地得知这个消息,以便使下回再通过位置
时选择正确的动作继续进入这个吃甜头的位置
。
可以看出,γ越大,小鸟就会越重视以往经验,越小,小鸟只重视眼前利益(R)。