来源:http://blog.csdn.net/lzhf1122/article/details/72935323
作者:lzhf1122
基础知识:
假设空间中两点x,y,定义:
欧几里得距离,
Mahalanobis距离,
不难发现,如果去掉马氏距离中的协方差矩阵,就退化为欧氏距离。那么我们就需要探究这个多出来的因子究竟有什么含义。
例子:
如果我们以厘米为单位来测量人的身高,以克(g)为单位测量人的体重。每个人被表示为一个两维向量,如一个人身高173cm,体重50000g,表示为(173,50000),根据身高体重的信息来判断体型的相似程度。
我们已知小明(160,60000);小王(160,59000);小李(170,60000)。根据常识可以知道小明和小王体型相似。但是如果根据欧几里得距离来判断,小明和小王的距离要远远大于小明和小李之间的距离,即小明和小李体型相似。这是因为不同特征的度量标准之间存在差异而导致判断出错。
以克(g)为单位测量人的体重,数据分布比较分散,即方差大,而以厘米为单位来测量人的身高,数据分布就相对集中,方差小。马氏距离的目的就是把方差归一化,使得特征之间的关系更加符合实际情况。
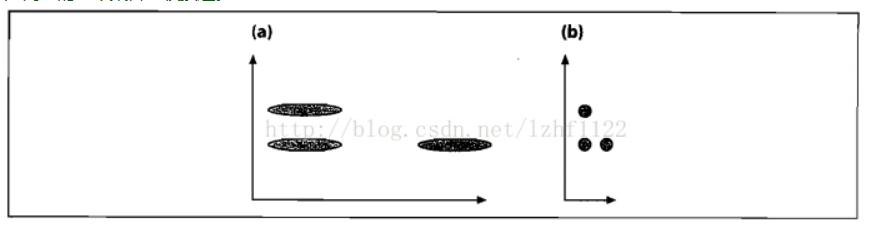
图(a)展示了三个数据集的初始分布,看起来竖直方向上的那两个集合比较接近。在我们根据数据的协方差归一化空间之后,如图(b),实际上水平方向上的两个集合比较接近。