轉自 https://blog.csdn.net/sinat_28576553/article/details/80258619
四个基本概念
TP、True Positive 真阳性:预测为正,实际也为正
FP、False Positive 假阳性:预测为正,实际为负
FN、False Negative 假阴性:预测与负、实际为正
TN、True Negative 真阴性:预测为负、实际也为负。
【一致判真假,预测判阴阳。】
以分类问题为例:

首先看真阳性:真阳性的定义是“预测为正,实际也是正”,这个最好理解,就是指预测正确,是哪个类就被分到哪个类。对类A而言,TP的个位数为2,对类B而言,TP的个数为2,对类C而言,TP的个数为1。
然后看假阳性,假阳性的定义是“预测为正,实际为负”,就是预测为某个类,但是实际不是。对类A而言,FP个数为0,我们预测之后,把1和2分给了A,这两个都是正确的,并不存在把不是A类的值分给A的情况。类B的FP是2,"3"和"8"都不是B类,但却分给了B,所以为假阳性。类C的假阳性个数为2。
最后看一下假阴性,假阴性的定义是“预测为负,实际为正”,对类A而言,FN为2,"3"和"4"分别预测为B和C,但是实际是A,也就是预测为负,实际为正。对类B而言,FN为1,对类C而言,FN为1。
具体情况看如下表格:
| A | B | C | 總計 | |
| TP | 2 | 2 | 1 | 5 |
| FP | 0 | 2 | 2 | 4 |
| FN | 2 | 1 | 1 | 4 |
精确率和召回率

计算我们预测出来的某类样本中,有多少是被正确预测的。针对预测样本而言。

针对原先实际样本而言,有多少样本被正确的预测出来了。
套用网上的一个例子:
某池塘有1400条鲤鱼,300只虾,300只鳖。现在以捕鲤鱼为目的。撒一大网,逮着了700条鲤鱼,200只虾,100只鳖。那么,这些指标分别如下:
精确率 = 700 / (700 +200 + 100) = 70%
召回率 = 700 / 1400 =50%
可以吧上述的例子看成分类预测问题,对于“鲤鱼来说”,TP真阳性为700,FP假阳性为300,FN假阴性为700。
Precison=TP/(TP+FP)=700(700+300)=70%
Recall=TP/(TP+FN)=700/(700+700)=50%
将上述例子,改变一下:把池子里的所有的鲤鱼、虾和鳖都一网打尽,观察这些指标的变化。
精确率 = 1400 / (1400 +300 + 300) = 70%
召回率 = 1400 / 1400 =100%
TP为1400:有1400条鲤鱼被预测出来;FP为600:有600个生物不是鲤鱼类,却被归类到鲤鱼;FN为0,鲤鱼都被归类到鲤鱼类去了,并没有归到其他类。
Precision=TP/(TP+FP)=1400/(1400+600)=70%
Recall=TP/(TP+FN)=1400/(1400)=100%
其实就是分母不同,一个分母是预测为正的样本数,另一个是原来样本中所有的正样本数。
作为预测者,我们当然是希望,Precision和Recall都保持一个较高的水准,但事实上这两者在某些情况下有矛盾的。比如极端情况下,我们只搜索出了一个结果,且是正确的,那么Precision就是100%,但是Recall就很低;而如果我们把所有结果都返回,那么比如Recall是100%,但是Precision就会很低。因此在不同的场合中需要自己判断希望Precision比较高或是Recall比较高,此时我们可以引出另一个评价指标—F1-Score(F-Measure)。
F1-Score
F1分数(F1 Score),是统计学中用来衡量二分类模型精确度的一种指标,用于测量不均衡数据的精度。它同时兼顾了分类模型的精确率和召回率。F1分数可以看作是模型精确率和召回率的一种加权平均,它的最大值是1,最小值是0。(出自百度百科)
数学定义:F1分数(F1-Score),又称为平衡F分数(BalancedScore),它被定义为精确率和召回率的调和平均数。
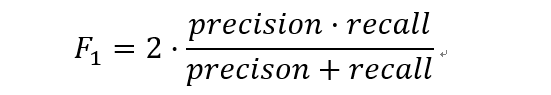
更一般的,我们定义Fβ分数为:
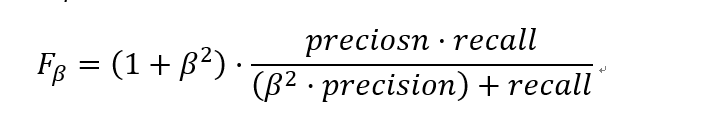
除了F1分数之外,F0.5分数和F2分数,在统计学中也得到了大量应用,其中,F2分数中,召回率的权重高于精确率,而F0.5分数中,精确率的权重高于召回率。
Micro-F1和Macro-F1
最后看Micro-F1和Macro-F1。在第一个多标签分类任务中,可以对每个“类”,计算F1,显然我们需要把所有类的F1合并起来考虑。
这里有两种合并方式:
第一种计算出所有类别总的Precision和Recall,然后计算F1。
例如依照最上面的表格来计算:Precison=5/(5+3)=0.625,Recall=5/(5+4)=0.556,然后带入F1的公式求出F1,这种方式被称为Micro-F1微平均。
第二种方式是计算出每一个类的Precison和Recall后计算F1,最后将F1平均。
例如上式A类:P=2/(2+0)=1.0,R=2/(2+2)=0.5,F1=(2*1*0.5)/1+0.5=0.667。同理求出B类C类的F1,最后求平均值,这种范式叫做Macro-F1宏平均。