Q:为什么会提及关于代价函数的理解?
A:在 ML 中线性回归、逻辑回归等总都是绕不开代价函数。
理解代价函数:是什么?作用原理?为什么代价函数是这个?
代价函数就是用于找到最优解的目的函数,这也是代价函数的作用。
损失函数(Loss Function )是定义在单个样本上的,算的是一个样本的误差。
代价函数(Cost Function )是定义在整个训练集上的,是所有样本误差的平均,也就是损失函数的平均。
目标函数(Object Function)定义为:最终需要优化的函数。等于经验风险+结构风险(也就是Cost Function + 正则化项)。
对于回归问题,我们需要求出代价函数来求解最优解,常用的是平方误差代价函数。
比如,对于下面的假设函数:

里面有 θ0 和 θ1 两个参数,参数的改变将会导致假设函数的变化,比如:

现实的例子中,数据会以很多点的形式给我们,我们想要解决回归问题,就需要将这些点拟合成一条直线,找到最优的 θ0 和 θ1 来使这条直线更能代表所有数据。
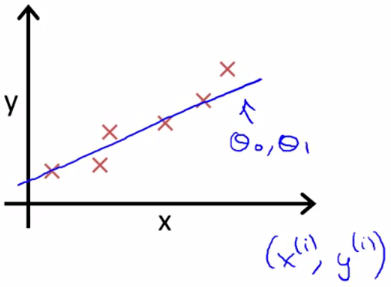
而如何找到最优解呢,就需要使用代价函数来求解了,以平方误差代价函数为例。
从最简单的单一参数来看,假设函数为:![]()
平方误差代价函数的主要思想就是将实际数据给出的值与我们拟合出的线的对应值做差,求出我们拟合出的直线与实际的差距。

为了使这个值不受个别极端数据影响而产生巨大波动,采用类似方差再取二分之一的方式来减小个别数据的影响。
这样,就产生了代价函数:
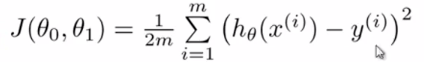
而最优解即为代价函数的最小值,根据以上公式多次计算可得到代价函数的图像:
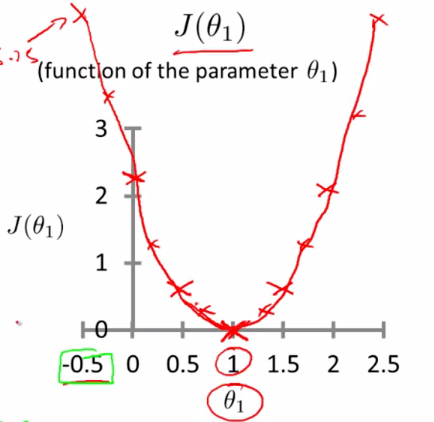
解(求导):可以看到该代价函数的确有最小值,这里恰好是横坐标为 1 的时候。
如果更多参数的话,就会更为复杂,两个参数的时候就已经是三维图像:
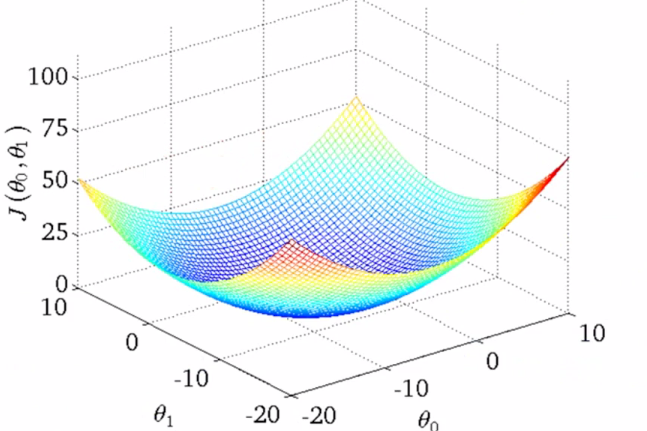
高度即为代价函数的值,可以看到它仍然有着最小值的,而到达更多的参数的时候就无法像这样可视化了,但是原理都是相似的。
因此,对于回归问题,我们就可以归结为得到代价函数的最小值:
首先思考:什么是代价?
简单理解代价就是预测值和实际值之间的差距(两点之间的距离),那对于多个样本来说,就是差距之和。
代价的正负问题:
如果直接使用,这个公式看起来就是表示假设值和实际值之差,再将每一个样本的这个差值加起来不就是代价了吗,但是想一下,如果使用这个公式,那么就单个样本而言,代价有正有负,全部样本的代价加起来有可能正负相抵,所以这并不是一个合适的代价函数。
解决有正有负的问题:
使用绝对值函数来表示代价,为了方便计算最小代价(计算最小代价可能用到最小二乘法),直接使用平方来衡量代价,即使用绝对值的平方来表示单个样本的代价,那么一个数据集的代价为: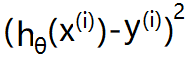
是否使用平方之和就没有什么问题了?
代价函数应该与样本的数量有关,否则一个样本和 m 个样本的差距平方和之间的比较也没有多少意义,所以将 m 个样本的代价之和 乘以 1/2m,即代价函数为:
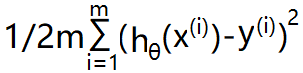
至于,取 2m 而非 m,是为了方便计算。