一些测试分型图形

http://www.fractalforums.com/3d-fractal-generation/true-3d-mandlebrot-type-fractal/msg8426/#msg8426REF:

https://www.iquilezles.org/www/articles/distance/distance.htm

一般求完f = SDF = 0，也就是等位面=0时候得  iossurface,平常做raymarching渲染用sdf渲染求交最方便。

这篇文章给了一个 叫做 "距离估算" ，实际上是zero-isosurface to x point distance.

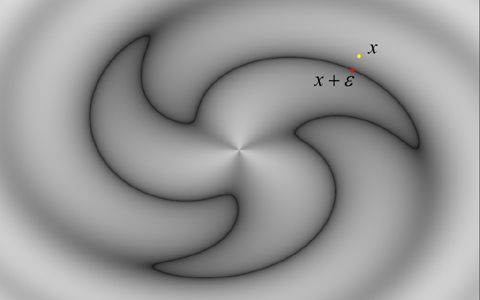
数学原理比较简单:

float smoothstep(float a; float b; float x){
    if (x<a) return 0.0f;
    if (x>=b) return 1.0f;
    float y = (x-a) / (b-a);
    return pow(y,2) *(3.0- 2.0 *y);
}


float f(vector pos)                                 
{
    float r = length(pos);
    float a = atan(pos.y,pos.x);
    return r - 1.0 + 0.5*sin(3.0*a  +  2.0*r*r);
} 


// grad dx=dy=dz
float dx = 0.01;

float xpos_l = @P.x + dx;
float xpos_r = @P.x - dx;

float ypos_l = @P.y + dx;
float ypos_r = @P.y - dx;

float zpos_l = @P.z + dx;
float zpos_r = @P.z - dx;


 
float gradx = ( f(set(xpos_l, @P.y, @P.z)) - f(set(xpos_r, @P.y, @P.z)) ) / (2 * dx);
float grady = ( f(set(@P.x, ypos_l, @P.z)) - f(set(@P.x, ypos_r, @P.z)) ) / (2 * dx);
float gradz = ( f(set(@P.x, @P.y, zpos_l)) - f(set(@P.x, @P.y, zpos_r)) ) / (2 * dx);

vector g = set(gradx,grady,gradz);
//@Cd = g;
//g = normalize(g);

float v = f(@P);

float de = abs(v) / length(g); //  distance estimation 
float eps = ch("distance");

//@Cd = smooth(1.9 * eps , 2.0 *eps , abs(v) );


@Cd = 1 - smooth(1 * eps , 2.0 *eps, de);

一些分型测试了:

1, 2d fractal based on complex operation:

REF:https://www.youtube.com/watch?v=MRuhHGYUJSI

 

 Houdini volumewrangle特别适合制作分形，由于仅仅判断一个length(vector) < ? 就可以得到一个sdf内部得density

如果是arnold得体积api也是一样简单。

2, 各种mandelbrot set分形测试

 REF:http://bugman123.com/Hypercomplex/#MandelbulbZ

<1>

 

 <2> Phase Shift ,make offset animation

REF:http://www.fractalforums.com/videos/3d-mandelbrot-set-phase-shift-animations/

Here is a way to continuously transform the negative z-component 3D Mandelbrot into the positive z-component Mandelbrot (with a rotation) by adding a phase shift:
{x,y,z}^n = r^n*{cos(phi)*cos(theta), cos(phi)*sin(theta), sin(phi)}
r=sqrt(x²+y²+z²), theta=n*atan2(y,x), phi=n*asin(z/r)+phase
where the phase varies continuously from goes from 0 to 2pi.

 another version

 3D Christmas Tree Mandelbrot Set,貌似这个是最漂亮的

n=2

 

n=8

对准菊花

 

MandelBar

4D Quaternion Mandelbrot ("Mandelquat")

从他得代码可以看到w初始值是0，在这个案例启示不用迭代w。

下面得julia是需要迭代得

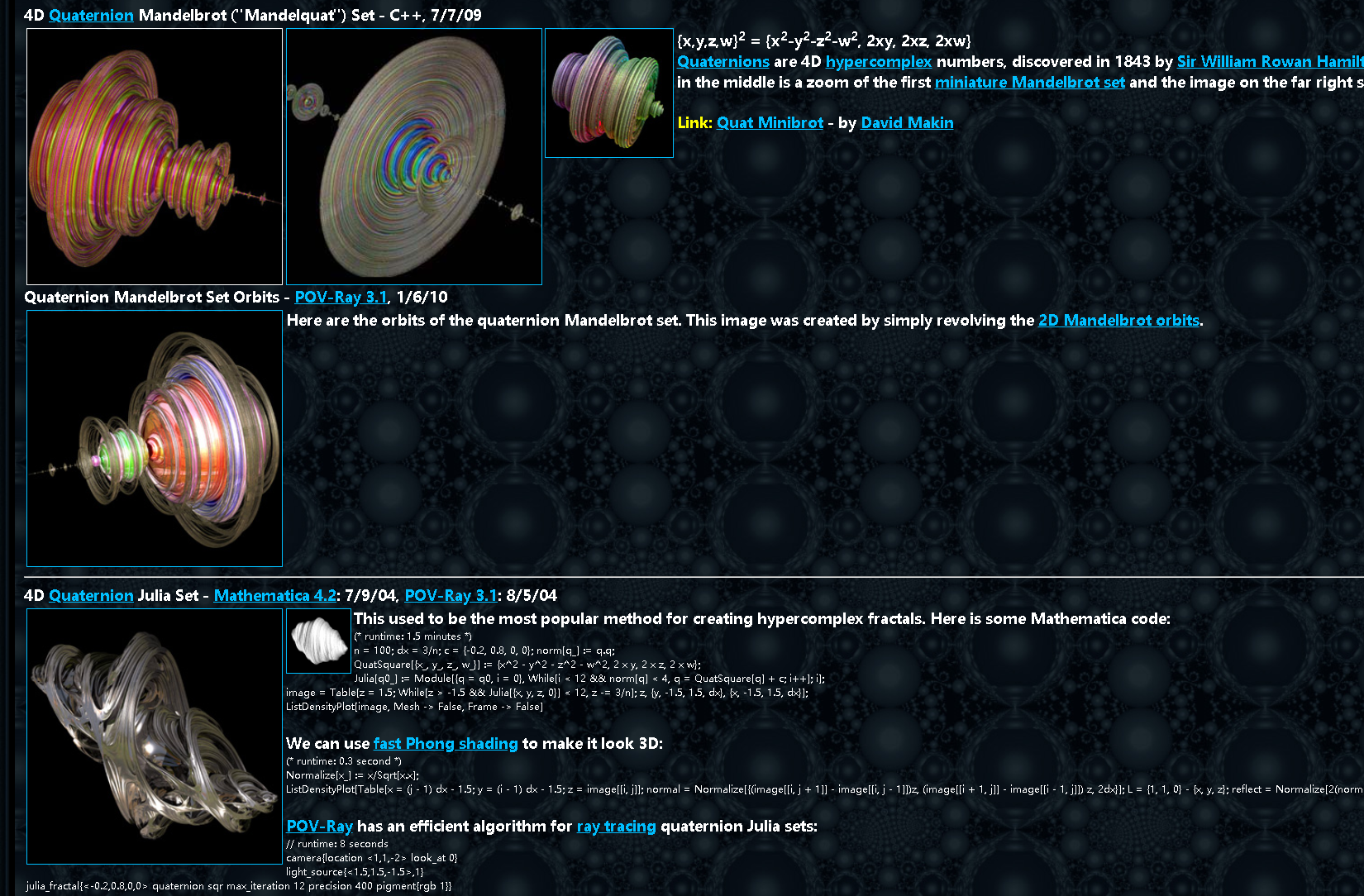
4D Quaternion Julia Set :

maxiter = 10

c = set(-0.8,0,0,,0)

 c = set(-0.8,0.2,0,0)

 c = set(-0.2,0.58,0,0)

c = set(-0.2,0.8,0,0)

4d bicomplex :

{x,y,z,w}2 = {x2-y2-z2+w2, 2(xy-zw), 2(xz-yw), 2(xw+yz)}

 这个里面我把 x*x + y*y + z*z + w*w > iters_num 取消了，因为最终给density 还是要判断  x*x + y*y + z*z + w*w < sqrt( x*x + y*y + z*z + w*w )

c = -0.2 0.5 0 0

 c = set(-0.01,0.8,0,0)

bicomplex_Mandelbrot_4d

 

4D Roundy_Mandelbrot:

 Roundy_julia

Mandelbrot set 3d:

{x,y,z}2 = {x2-y2-z2, 2xy, 2(x-y)z}