复习基础知识
1,GLSL Mat矩阵全部是列向量 优先构造矩阵。
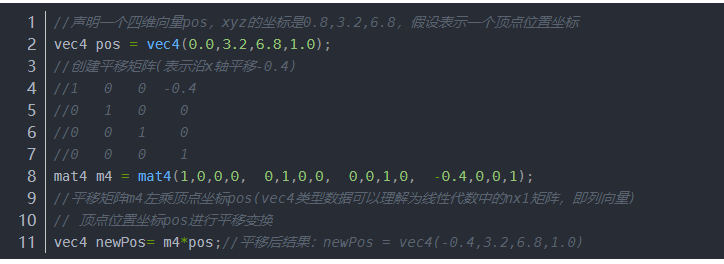
2,GLM同样以列为主:
#include <iostream> #include <glm/glm.hpp> #include <glm/gtc/matrix_transform.hpp> #include <glm/gtc/type_ptr.hpp> using namespace std;
ostream & operator<<(ostream & os , const glm::mat4 &inputMat){ // col:1 row:1 col:2 row:1 col:3 row:1 col:4 row:1 cout << inputMat[0][0] <<" " <<inputMat[1][0] << " " <<inputMat[2][0] << " " << inputMat[3][0] << endl; // col:1 row:2 col:2 row:2 col:3 row:2 col:4 row:2 cout << inputMat[0][1] <<" " <<inputMat[1][1] << " " <<inputMat[2][1] << " " << inputMat[3][1] << endl; // col:1 row:3 col:2 row:3 col:3 row:3 col:4 row:3 cout << inputMat[0][2] <<" " <<inputMat[1][2] << " " <<inputMat[2][2] << " " << inputMat[3][2] << endl; // col:1 row:4 col:2 row:4 col:3 row:4 col:4 row:4 cout << inputMat[0][3] <<" " <<inputMat[1][3] << " " <<inputMat[2][3] << " " << inputMat[3][3] << endl; return os; } ostream & operator << (ostream &os , const glm::vec4 &vec){ cout << vec.x << " " << vec.y << " " << vec.z << " " <<vec.w ; return os; } void debug(const glm::mat4 &inputMat){ cout << "col 1->" <<inputMat[0] << endl; // access col 1 cout << "col 2->" <<inputMat[1] << endl; // access col 2 cout << "col 3->" <<inputMat[2] << endl; // access col 3 cout << "col 4->" <<inputMat[3] << endl; // access col 4 } int main() { glm::mat4 m01(1.0f); cout << m01 <<endl; // use array to construct matrix glm::mat4 m02(1,2,3,4, 5,6,7,8, 9,10,11,12, 13,14,15,16); cout << m02 << endl; // Use vector to construct matrix glm::mat4 m03(glm::vec4(1,1,1,1), glm::vec4(2,2,2,2), glm::vec4(3,3,3,3), glm::vec4(4,4,4,4)); cout << m03 << endl; debug(m03); return 0; }
结果:
D:plugin_devopenglglm_testCP_01cmake-build-debugCP_01.exe 1 0 0 0 0 1 0 0 0 0 1 0 0 0 0 1 1 5 9 13 2 6 10 14 3 7 11 15 4 8 12 16 1 2 3 4 1 2 3 4 1 2 3 4 1 2 3 4 col 1->1 1 1 1 col 2->2 2 2 2 col 3->3 3 3 3 col 4->4 4 4 4 Process finished with exit code 0
3,同样观查GLM源码,operator[]确实返回列为主得向量
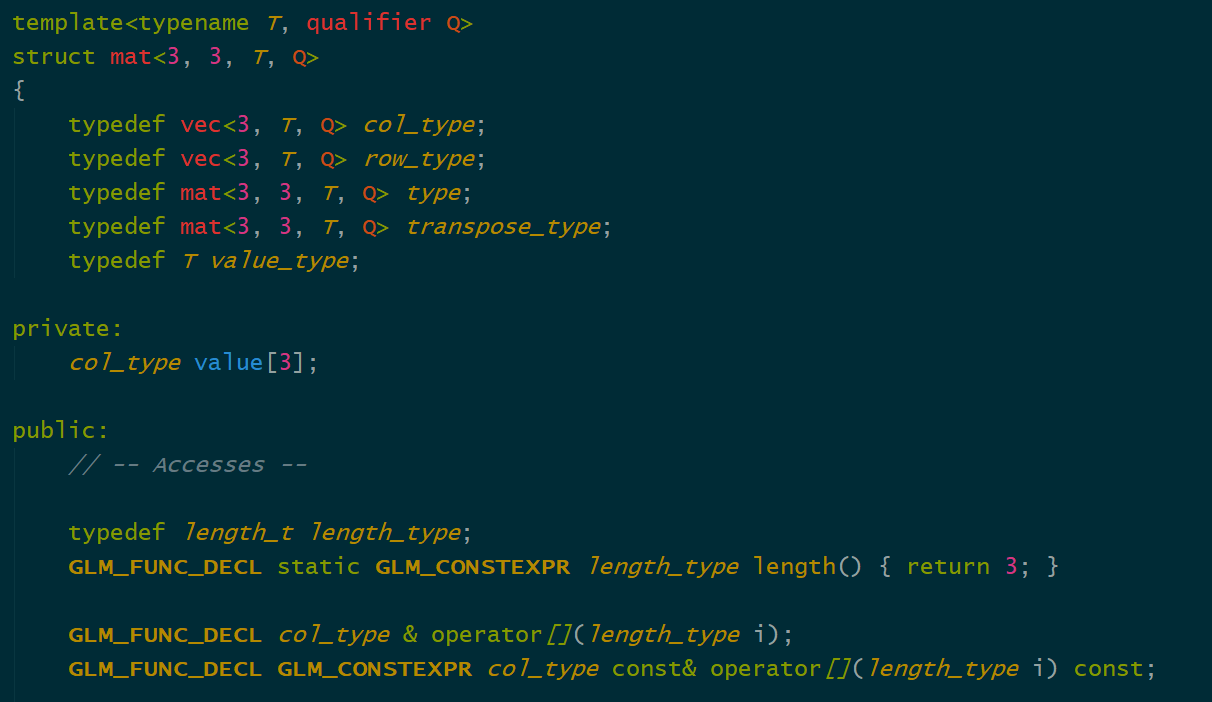
4,把GLM向量放到vector中,展平访问:
#include <iostream> #include <glm/gtc/matrix_transform.hpp> #include <glm/gtc/type_ptr.hpp> #include <glm/glm.hpp> #include <vector> using namespace std; int main() { vector <glm::vec3> points; points.emplace_back(glm::vec3(1,2,3)); points.emplace_back(glm::vec3(4,5,6)); points.emplace_back(glm::vec3(7,8,9)); float *dataPointer = (float*) (points.data()); cout << *( dataPointer + 0) << endl; // -> 1 cout << *( dataPointer + 1) << endl; // -> 2 cout << *( dataPointer + 2) << endl; // -> 3 cout << *( dataPointer + 3) << endl; // -> 4 return 0; }
5,而我们houdini却是个用行向量。
6, NormalMap:
Houdini需要normalMalMap:

OPENGL需要的NormalMap,可以看到Y轴向是反的:

https://learnopengl-cn.github.io/05%20Advanced%20Lighting/04%20Normal%20Mapping/ 给的贴图必须在Houdini下选择linear 模式。
首先 法线贴图是在切线空间,在切线空间法线全部对齐z轴向。
用houdini理解最简单,平常一个物体比如box对齐到z轴向。如图:

如果把这玩意拷贝到球上:相当于将把长方体 转到 法线形成的正交矩阵空间,此时这个法线空间就是我们的世界空间,(一般用个up向量和这个球上法线形成3个正交向量就行,但是也可以是TBN矩阵):


当然转到 这个球的法线空间(世界物体法线空间),也可以形成TBN正交矩阵:

Houdini IMP the normalMap at world space:
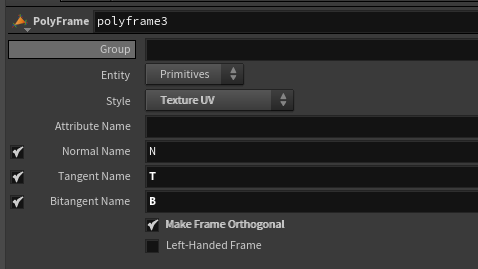
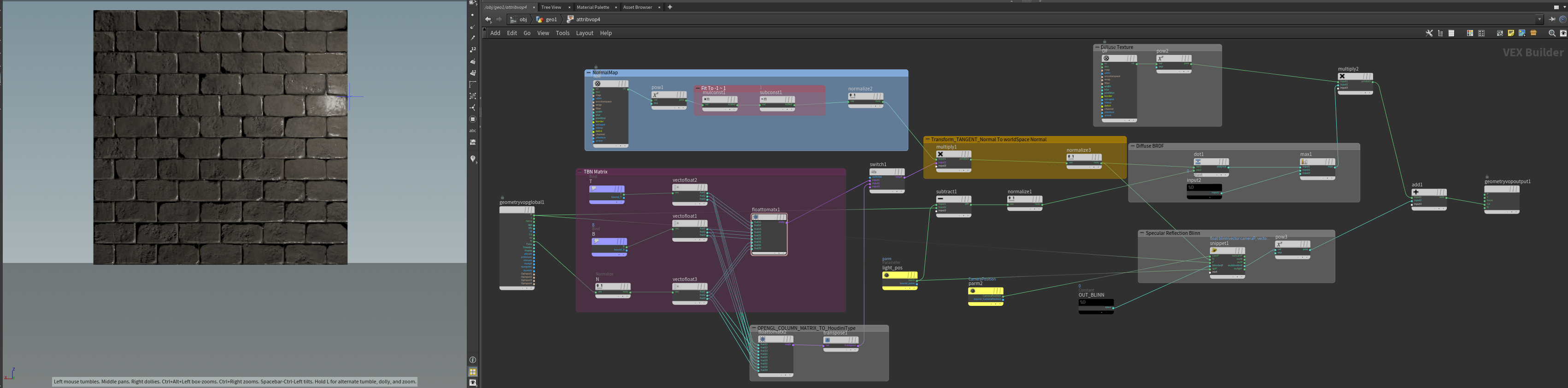

float blinn(vector cameraP; vector P; vector N; vector LgtP){ vector wo = normalize(cameraP - P); vector wi = normalize(LgtP - P); vector nn = normalize(N); // cal the blinn specular vector h = normalize(wi + wo); float ndoth = max(dot(nn,h),0.0f); float blinn_brdf = pow(ndoth,60.0f) ; return blinn_brdf; } blinnbrdf = blinn(camP,P,N,lgtP);
所以:
1,只要把 TBN矩阵 * 法线贴图形成的vector 相当于把法线贴图转到真正的 世界空间可以直接用的法线,此时这个法线做灯光用,细节多的一批。
2,也可以直接把世界空间的向量(比如灯光向量)变换到这个法线贴图所在的 切线空间。方法就是TBN的逆矩阵 * 灯光向量,而正交矩阵的逆矩阵=正交矩阵的转置矩阵,求逆矩阵运算量太大,所以教程中也是转到转置矩阵。接下来就是正常的材质运算。
