超越函数/微分方程 /积分中的技术/级数

大纲:
<1>自然对数函数: y=lnx的导数

<2>lnx的值阈

<3>积分1/u du , 积分tanu,cotu

<4>对数微分法 

<5>log以a为底u的导数

<6>含有log以a为底x的积分。

知识点:

<1>d/dx (lnx)  =  d/dx ∫(1/t dt) = 1/x     t 属于[1,x]

<2>如何求ln2的值，用以前学过的辛普森,梯形法

<3>∫1/u du = ln|u| + C

<4>∫ u^n  du =  1/(n+1) * u^(n+1)   这个公式仅仅是n!=-1 时候成立

<5>如果4中的n=-1如何求  那么就会变成 ∫u^-1 du = ln|u|   

1，数列

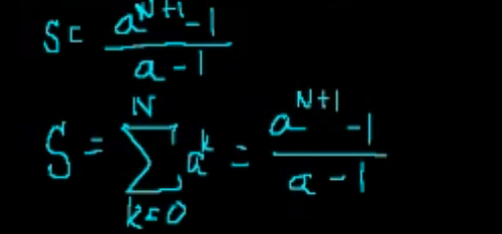
a = 1/2 时, N->正无穷 , S->2

float lens = length(@P);
@P.y += ( pow(0.5,lens) - 1.0f) / (0.5-1);

<2>求lnx 的值，如何求ln2,ln3,ln4 ,利用simpson法则或者Trapezoidal(梯形法),再次粘贴python代码:

import math


# Trapezoidal
# S = 1/2(y0+ 2y1 + 2y2 + 2y3+...+ 2yn-1 + yn)

def Trapezoidal(down,up,n,func):
    if up==down:
        return 0.0
    h = float(up-down) / float(n)
    start = func(down)
    end = func(up)

    process = 0.0
    for dt in xrange(0,n+1,1):
        if dt == 0 or dt == n:
            continue
        process += 2 * func(down + dt * h)
    sum =  (start + end + process) * (h/2.0)
    return sum



# Simpson
# S = h/3(y0 + 4y1 + 2y2 + 4y3 + 2y4 + ... + 2yn-1 + yn)
# func is f(x)
def Simpson(down,up,n,func):
    if up==down:
        return 0.0
    h = float(up-down) / float(n)
    start = func(down)
    end = func(up)
    process = 0.0
    for dt in xrange(0,n+1,1):
        if dt == 0 or dt == n:
            continue
        # select the 1 3 5 7 9... index
        if dt%2 == 1:
            process += 4 * func(down + dt * h)
        # select the 2 4 6 8 10... index
        if dt%2 == 0:
            process += 2 * func(down + dt * h)

    sum =  (start + end + process) * (h/3.0)
    return sum

求ln2

lnx = lambda x: 1/x
print Simpson(1,2,100,lnx);

<3>一阶可分离变量微分方程

解微分方程y' = y

y = C * e^x

<4>欧拉法:

y' = 1 + x  ； y(0) = 1 ; 带初值条件。并不需要知道 y = ? 

类似这样的公式，一般方法求到 公式 y = ? 原型，然后就可以计算y(n) = ?

在欧拉法里就不需用，感觉跟牛顿迭代法是一个货色，都用的线性化公式。

下面是一个改进的欧拉法:

python code:

import numpy as np

def Euler(func, X0, Y0, perspectiveX, dx = 0.1,debug=True):
    if perspectiveX == X0:
        return Y0
    # improve Euler method
    # Xn = Xn-1 + dx
    # Zn = Yn-1 + f(Xn-1, Yn-1) * dx
    # Yn = Yn-1 + [ f(Xn-1, Yn-1) + f(Xn,Zn) / 2 ] * dx

    Xn = X0
    Zn = Y0
    Yn = Y0
    for it in np.arange(X0, perspectiveX, dx):
        if debug:
            print "-----------loop------------------" , it
        Xn = Xn + dx # 1:X0 + dx , 2:X0 + dx + dx  ...
        if debug:
            print "Xn" , Xn

        Zn = Yn + func(Yn) * dx

        Yn = Yn + ( (func(Yn) + func(Zn)) / 2.00) * dx
        if debug:
            print "Yn", Yn
    return Yn

print "Result :" , Euler(lambda y: 1+y , 0.0, 1.0 , 1, )

<5>来源:Proof witout words! by fouad Nakhil

pi^e < e ^pi

有方程 : y = lnx/x  (画图得下面公式)

lne/e > lnpi / pi

移项 得pi^e < e ^pi

<6> Nopier 不等式:

 <7>动脉与小血管分叉度对血液摩擦力 造成的动能损失问题。

积分技术:

1,替换法

2,展开幂指数 例如(secx + tanx)^2 dx 这样的一定要展开

3,消除平方根 

 4，化简假分式,就是分子的次数高于或者等于分母的次数

 5,分步积分

 6,分步积分扩展:列表积分法:

级数:Cauchy浓缩判别法:

证明：