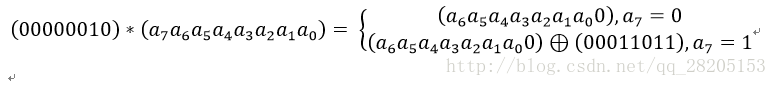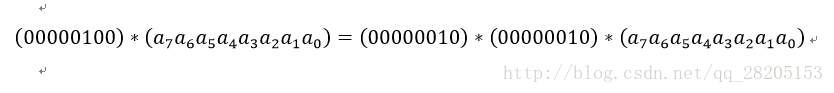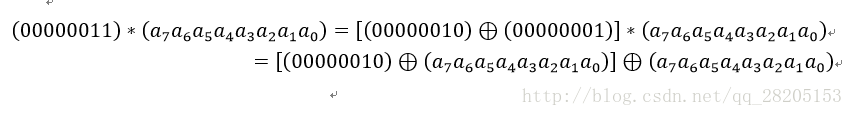密码学——AES加密算法
AES加密算法就是众多对称加密算法中的一种,它的英文全称是Advanced Encryption Standard,翻译过来是高级加密标准,它是用来替代之前的DES加密算法的。AES加密算法采用分组密码体制,每个分组数据的长度为128位16个字节,密钥长度可以是128位16个字节、192位或256位,一共有四种加密模式,我们通常采用需要初始向量IV的CBC模式,初始向量的长度也是128位16个字节。
概念
域的概率及性质
形象地说,域有这样一个性质:在加法和乘法上具有封闭性。也就是说对域中的元素进行加法或乘法运算后的结果仍然是域中的元素。
域有单位元和逆元两个概念。加法和乘法运算都有对应的单位元(这两个单位元一般不同,但都用符号e表示)。单位元就像线性代数的单位矩阵。一个矩阵乘以单位矩阵等于本身。对应地,在域中的单位元有:对于加法单位元,所有元素加上单位元e,等于其本身。对应乘法单位元,所有元素乘上单位e,等于其本身。
逆元就像数学上的倒数,两个元素互为对方的逆元。如果元素a和b互为加法逆元,那么就有 a + b = e。若互为乘法逆元,那么就有a * b = e。如果元素a在域中找不到另外一个元素b,使得a+b=e(a*b=e),那么a就没有加法(乘法)逆元。。
有限域GF(p)
在密码学中,有限域GF(p)是一个很重要的域,其中p为[素数](javascript:void())。简单来说,GF(p)就是 mod p,因为一个数 模p后,结果在[0, p-1]之间。对于元素a和b,那么(a+b) mod p和(a*b)mod p,其结果都是域中的元素。GF(p)里面的加法和乘法都是平时用的加法和乘法。GF(p)的加法和乘法单位元分别是0和1,元素的加法和乘法逆元都很容易理解和求得。
GF(2^8)的加法和乘法
加法就是经典的异或运算;乘法则稍复杂一些,对于一个8位的二进制数来说,使用域上的乘法乘以(00000010)等价于左移1位(低位补0)后,再根据情况同(00011011)进行异或运算,设S1 = (a7 a6 a5 a4 a3 a2 a1 a0),刚0x02 * S1如下图所示:
也就是说,如果a7为1,则进行异或运算,否则不进行。
类似地,乘以(00000100)可以拆分成两次乘以(00000010)的运算:
乘以(0000 0011)可以拆分成先分别乘以(0000 0001)和(0000 0010),再将两个乘积异或:
因此,我们只A需要实现乘以2的函数,其他数值的乘法都可以通过组合来实现。
AES加密流程
AES 加密算法A大致分为 4 个步骤:
(1)字节替代
(2)行移位
(3)列混淆
(4)轮密相加
加解密中每轮的密钥分别由初始密钥扩展得到。算法中16字节的明文、密文和轮密钥都以一个4x4的矩阵表示。加密流程图如下:

下面详细介绍每一种操作
-
字节代换
字节代替的主要功能是通过S盒完成一个字节到另外一个字节的映射。下图(a)为S盒,图(b)为S-1(S盒的逆)。
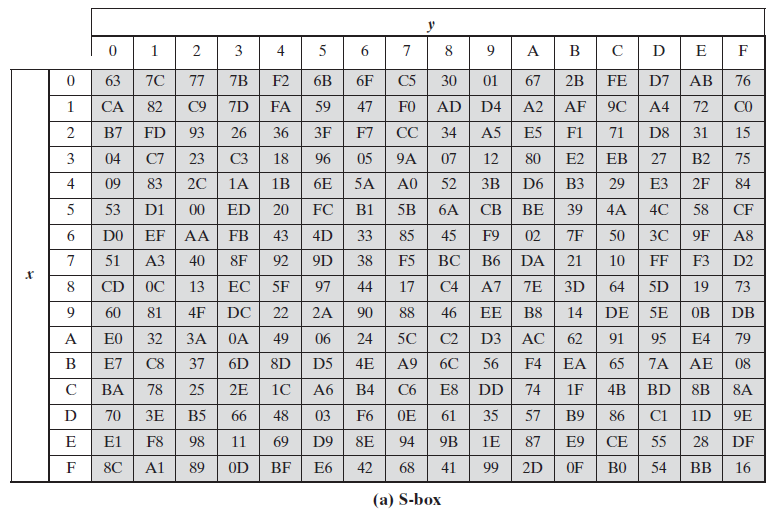

(S)和(S^{-1})分别为16x16的矩阵。假设输入字节的值为a=a7a6a5a4a3a2a1a0,则输出值为S[a7a6a5a4][a3a2a1a0],S-1的变换也同理。
-
行移位
行移位的功能是实现一个4x4矩阵内部字节之间的置换。
正向行移位的原理图如下:

实际移位的操作即是:第一行保存不变,第二行循环左移1个字节,第三行循环左移2个字节,第四行循环左移3个字节。假设矩阵的名字为state,用公式表示如下:(state[i][j] = state[i][(j+i)%4];)其中i、j属于[0,3]。
逆向行移位即是相反的操作,用公式表示如下:(state[i][j] = state[i][(4+j-i)%4]);其中i、j属于[0,3]。
-
列混淆
列混淆:利用(GF(2^8))域上算术特性的一个代替,正向列混淆的原理图如下:

根据矩阵的乘法可知,在列混淆的过程中,每个字节对应的值只与该列的4个值有关系。此处的乘法和加法都是定义在GF(28)上的,需要注意如下几点:
-
将某个字节所对应的值乘以2,其结果就是将该值的二进制位左移一位,如果该值的最高位为1(表示该数值不小于128),则还需要将移位后的结果异或00011011
-
乘法对加法满足分配率,例如:(07·S_{0,0}=(01⊕02⊕04)·S_{0,0}= S0,0⊕(02·S_{0,0}(04·S_{0,0}))
-
此处的矩阵乘法与一般意义上矩阵的乘法有所不同,各个值在相加时使用的是模2加法(相当于是异或运算)。
-
-
轮密相加
任何数和自身的异或结果为0。加密过程中,每轮的输入与轮密钥异或一次;因此,解密时再异或上该轮的密钥即可恢复输入。
-
密钥扩展
密钥扩展的原理图如下:

密钥扩展过程说明:
- 将初始密钥以列为主,转化为4个32 bits的字,分别记为w[0…3];、
- 按照如下方式,依次求解w[j],其中j是整数并且属于[4,43];
- 若j%4=0,则w[j]=w[j-4]⊕g(w[j-1]),否则w[j]=w[j-4]⊕w[j-1];
函数g的流程说明:
- 将w循环左移一个字节;
- 分别对每个字节按S盒进行映射;
- 与32 bits的常量(RC[j/4],0,0,0)进行异或,RC是一个一维数组,其值如下。(RC的值只需要有10个,而此处用了11个,实际上RC[0]在运算中没有用到,增加RC[0]是为了便于程序中用数组表示。由于j的最小取值是4,j/4的最小取值则是1,因此不会产生错误。)
RC = {00, 01, 02, 04, 08, 10, 20, 40, 80, 1B, 36}
Python实现
密码学——AES加密算法
AES加密算法就是众多对称加密算法中的一种,它的英文全称是Advanced Encryption Standard,翻译过来是高级加密标准,它是用来替代之前的DES加密算法的。AES加密算法采用分组密码体制,每个分组数据的长度为128位16个字节,密钥长度可以是128位16个字节、192位或256位,一共有四种加密模式,我们通常采用需要初始向量IV的CBC模式,初始向量的长度也是128位16个字节。
概念
域的概率及性质
形象地说,域有这样一个性质:在加法和乘法上具有封闭性。也就是说对域中的元素进行加法或乘法运算后的结果仍然是域中的元素。
域有单位元和逆元两个概念。加法和乘法运算都有对应的单位元(这两个单位元一般不同,但都用符号e表示)。单位元就像线性代数的单位矩阵。一个矩阵乘以单位矩阵等于本身。对应地,在域中的单位元有:对于加法单位元,所有元素加上单位元e,等于其本身。对应乘法单位元,所有元素乘上单位e,等于其本身。
逆元就像数学上的倒数,两个元素互为对方的逆元。如果元素a和b互为加法逆元,那么就有 a + b = e。若互为乘法逆元,那么就有a * b = e。如果元素a在域中找不到另外一个元素b,使得a+b=e(a*b=e),那么a就没有加法(乘法)逆元。。
有限域GF(p)
在密码学中,有限域GF(p)是一个很重要的域,其中p为[素数](javascript:void())。简单来说,GF(p)就是 mod p,因为一个数 模p后,结果在[0, p-1]之间。对于元素a和b,那么(a+b) mod p和(a*b)mod p,其结果都是域中的元素。GF(p)里面的加法和乘法都是平时用的加法和乘法。GF(p)的加法和乘法单位元分别是0和1,元素的加法和乘法逆元都很容易理解和求得。
GF(2^8)的加法和乘法
加法就是经典的异或运算;乘法则稍复杂一些,对于一个8位的二进制数来说,使用域上的乘法乘以(00000010)等价于左移1位(低位补0)后,再根据情况同(00011011)进行异或运算,设S1 = (a7 a6 a5 a4 a3 a2 a1 a0),刚0x02 * S1如下图所示:
也就是说,如果a7为1,则进行异或运算,否则不进行。
类似地,乘以(00000100)可以拆分成两次乘以(00000010)的运算:
乘以(0000 0011)可以拆分成先分别乘以(0000 0001)和(0000 0010),再将两个乘积异或:
因此,我们只A需要实现乘以2的函数,其他数值的乘法都可以通过组合来实现。
AES加密流程
AES 加密算法A大致分为 4 个步骤:
(1)字节替代
(2)行移位
(3)列混淆
(4)轮密相加
加解密中每轮的密钥分别由初始密钥扩展得到。算法中16字节的明文、密文和轮密钥都以一个4x4的矩阵表示。加密流程图如下:

下面详细介绍每一种操作
-
字节代换
字节代替的主要功能是通过S盒完成一个字节到另外一个字节的映射。下图(a)为S盒,图(b)为S-1(S盒的逆)。


(S)和(S^{-1})分别为16x16的矩阵。假设输入字节的值为a=a7a6a5a4a3a2a1a0,则输出值为S[a7a6a5a4][a3a2a1a0],S-1的变换也同理。
-
行移位
行移位的功能是实现一个4x4矩阵内部字节之间的置换。
正向行移位的原理图如下:

实际移位的操作即是:第一行保存不变,第二行循环左移1个字节,第三行循环左移2个字节,第四行循环左移3个字节。假设矩阵的名字为state,用公式表示如下:(state[i][j] = state[i][(j+i)%4];)其中i、j属于[0,3]。
逆向行移位即是相反的操作,用公式表示如下:(state[i][j] = state[i][(4+j-i)%4]);其中i、j属于[0,3]。
-
列混淆
列混淆:利用(GF(2^8))域上算术特性的一个代替,正向列混淆的原理图如下:

根据矩阵的乘法可知,在列混淆的过程中,每个字节对应的值只与该列的4个值有关系。此处的乘法和加法都是定义在GF(28)上的,需要注意如下几点:
-
将某个字节所对应的值乘以2,其结果就是将该值的二进制位左移一位,如果该值的最高位为1(表示该数值不小于128),则还需要将移位后的结果异或00011011
-
乘法对加法满足分配率,例如:(07·S_{0,0}=(01⊕02⊕04)·S_{0,0}= S0,0⊕(02·S_{0,0}(04·S_{0,0}))
-
此处的矩阵乘法与一般意义上矩阵的乘法有所不同,各个值在相加时使用的是模2加法(相当于是异或运算)。
-
-
轮密相加
任何数和自身的异或结果为0。加密过程中,每轮的输入与轮密钥异或一次;因此,解密时再异或上该轮的密钥即可恢复输入。
-
密钥扩展
密钥扩展的原理图如下:

密钥扩展过程说明:
- 将初始密钥以列为主,转化为4个32 bits的字,分别记为w[0…3];、
- 按照如下方式,依次求解w[j],其中j是整数并且属于[4,43];
- 若j%4=0,则w[j]=w[j-4]⊕g(w[j-1]),否则w[j]=w[j-4]⊕w[j-1];
函数g的流程说明:
- 将w循环左移一个字节;
- 分别对每个字节按S盒进行映射;
- 与32 bits的常量(RC[j/4],0,0,0)进行异或,RC是一个一维数组,其值如下。(RC的值只需要有10个,而此处用了11个,实际上RC[0]在运算中没有用到,增加RC[0]是为了便于程序中用数组表示。由于j的最小取值是4,j/4的最小取值则是1,因此不会产生错误。)
RC = {00, 01, 02, 04, 08, 10, 20, 40, 80, 1B, 36}