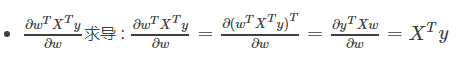问题
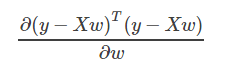
说明: y、w为列向量,X为矩阵
式子演化
看到这个例子不要急着去查表求导,先看看它的形式,是u(w)∗v(w)的形式,这种形式一般求导较为复杂,因此为了简化运算,我们先把式子展开成下面的样子(注意:(Xw)T=wTXT):
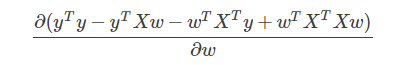
然后就可以写成四个部分求导的形式如下(累加后求导=求导后累加):
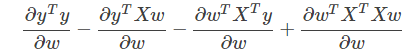
求导
说明:分子部分为标量,分母部分为向量,找到维基百科中的Scalar-by-vector identities表格,在表格中匹配形式到第1行的位置,因为分母为列向量,因此为分母布局,对应的求导结果就是 0 。
说明:同样的,在维基百科中的Scalar-by-vector identities表格,在表格中匹配形式到第11行的位置,对应的求导结果就是 XTy 。
说明:因为分子为标量,标量的转置等于本身,所以对分子进行转置操作,其等价于第二部分。
说明:同样的,在维基百科中的Scalar-by-vector identities表格,在表格中匹配形式到第13行的位置,矩阵的转置乘上本身(XTX)为对称矩阵当做表格中的A ,所以得到求导结果 2XTXw 。
整合
把四个部分求导结果进行相应的加减就可以得到最终的结果:
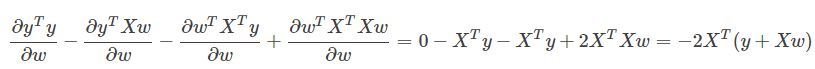
得解