1.准对角阵
准对角阵的形式如下:
由于我们知道A所对应的行列式的值等于每一个分块A行列式的值的乘积,同时假设我们的A矩阵是可逆矩阵的话,则A矩阵所对应的行列式的值一定不等于零,又有公式: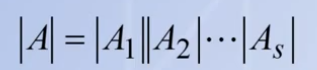
所以我们可以导出,A矩阵当中的每一个小分块矩阵都是可逆的,因为它们每一个矩阵所对应的行列式的值都不等于零,不然大A矩阵的行列式就等零了,数学结论如下: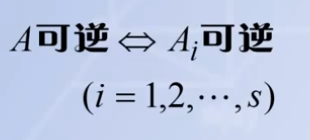
我们且有公式:

这个公式利用A的负一次幂乘以A等于单位矩阵E就可以得到证明了。同时也有有关矩阵的秩的公式,大的矩阵的秩等于分块矩阵的秩的和: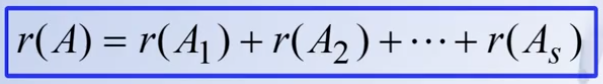
如果是方阵,还能够求出它的行列式的值,是非奇异矩阵的话,那么其矩阵的秩直接就等于方阵的阶数了,并不需要求出每一个分块矩阵的值的和。非方阵的求法就要用上述公式了。
2.分块三角阵
分块三角阵的计算公式以及性质:
求上三角阵的逆的公式:

求下三角阵的公式:

3.分块斜对角阵
形式如下: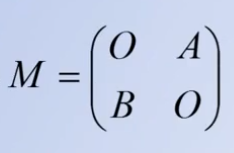
同样的,这个特殊的分块矩阵也有如下性质:
求解这个矩阵的逆的公式是:
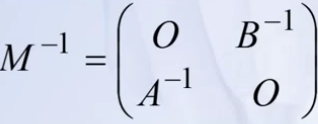
上面就是三种特殊的三角阵的求法了。