我们先建立一棵简单的二叉树:
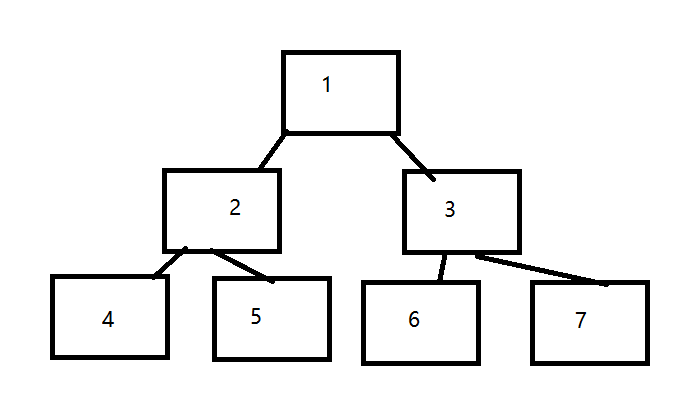
代码如下所示:
class TreeNode: def __init__(self, x): self.val = x self.left = None self.right = None l1 = TreeNode(1) l2 = TreeNode(2) l3 = TreeNode(3) l4 = TreeNode(4) l5 = TreeNode(5) l6 = TreeNode(6) l7 = TreeNode(7) l1.left = l2 l1.right = l3 l2.left = l4 l2.right = l5 l3.left = l6 l3.right = l7
然后进行先序遍历:
def pretravale(treenode): if treenode==None: return None print(treenode.val) pretravale(treenode.left) pretravale(treenode.right)
中序:
#利用深度优先搜索进行中序遍历 def midtravale(treenode): if treenode==None: return None midtravale(treenode.left)#先往左走到底,然后打印根节点 print(treenode.val) midtravale(treenode.right)
后序:
def latetravale(treenode): if treenode == None: return None latetravale(treenode.left) latetravale(treenode.right) print(treenode.val)
打印遍历结果:
pretravale(l1) print("开始中序遍历") midtravale(l1) print("开始后序便遍历") latetravale(l1)
得到:
1 2 4 5 3 6 7 开始中序遍历 4 2 5 1 6 3 7 开始后序便遍历 4 5 2 6 7 3 1
当然面试官看到你使用递归解法来遍历这棵树肯定是不满意的,因此这里给出对这棵树的迭代解法,首先是先序遍历,在遍历的时候我们可以一直往左进行入栈,当栈中没有元素可以添加之后,也就是树的左端的元素已经没了变成了None,那么我们弹出最尾端的元素,如果说最尾端有元素的话就再次对最尾端的元素的left进行遍历,如果没有则返回到上一级的树根。
# 使用非递归的方式进行先序遍历 def preOrder(root): if root==None: return None stack=[] tmpNode=root while tmpNode or stack:#不能为空 while tmpNode: print(tmpNode.val) stack.append(tmpNode) tmpNode=tmpNode.left#继续找这个跟节点的左子树 #将左子树一直放到里面,直到没有左子树 node = stack.pop() tmpNode = node.right# 假设node.right为空则tmpNode也为空 #如果不为空的话,那么node.right就赋值给新的tmpNode
中序遍历我们改变一下打印的顺序就好了,毕竟都是深度优先搜索(DFS):
#中序遍历 def midOrder(root): if root==None: return None stack=[] tmpNode=root while tmpNode or stack:#不能为空 while tmpNode: #print(tmpNode.val) stack.append(tmpNode) tmpNode=tmpNode.left#继续找这个跟节点的左子树 #将左子树一直放到里面,直到没有左子树 node = stack.pop() print(node.val) tmpNode = node.right# 假设node.right为空则tmpNode也为空 #如果不为空的话,那么node.right就赋值给新的tmpNode
后续遍历的迭代解法可以留给大家自己去思考