一.最常见的self-attention
对于自注意力机制而言,我们有的时候会遇到词性分类的任务,比如说给定一句话,我想知道这句话当中每一个单词的词性。但是使用双向lstm呢,会有很多信息被忽略掉,尤其是一些位于后面的词很可能前面的词对它的影响没有那么大,即使我们的lstm考虑了一些遗忘门,增强记忆的一些机制,位于最前面的单词和最后面的单词之间始终是具有一定距离的,而self-attnetion则可以直接对收尾的单词计算其相关性,没有任何的数据损失。因此我们可以采用自注意力机制,也就是self-attention来解决这个问题。同时self-attention在transformer当中也有着广泛的应用。
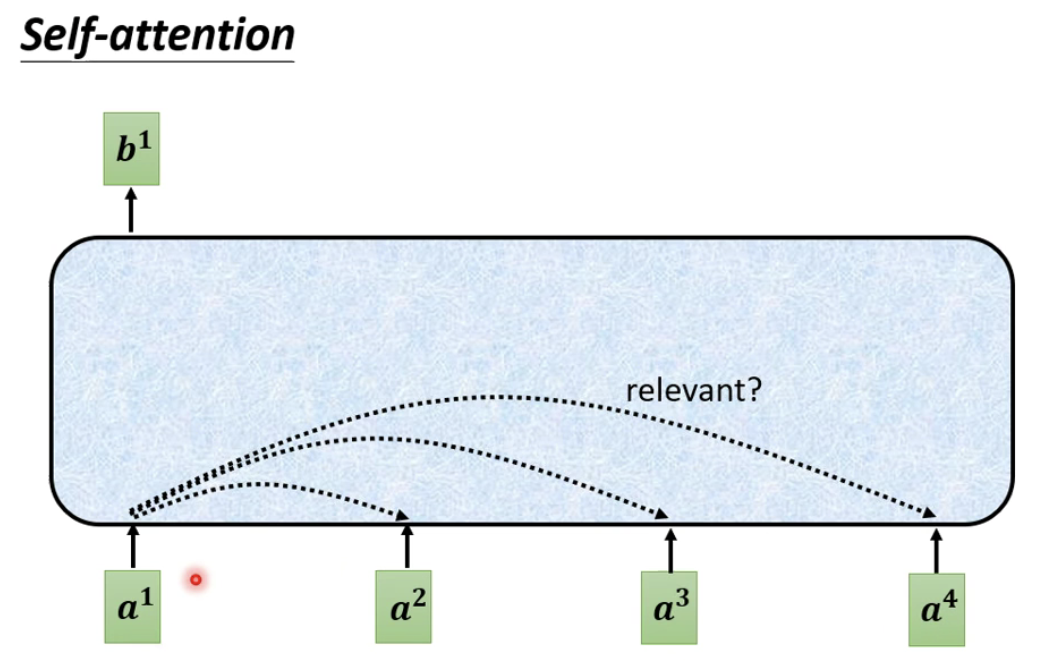
如上图所示,蓝色部分表示self-attention,首先我们self-attention找到每一个向量之间的联系,看是否考虑某一个向量对第一个向量a1会产生影响。而我们可以通过如下的方法来计算两个向量之间的相关联程度。如下图所示:
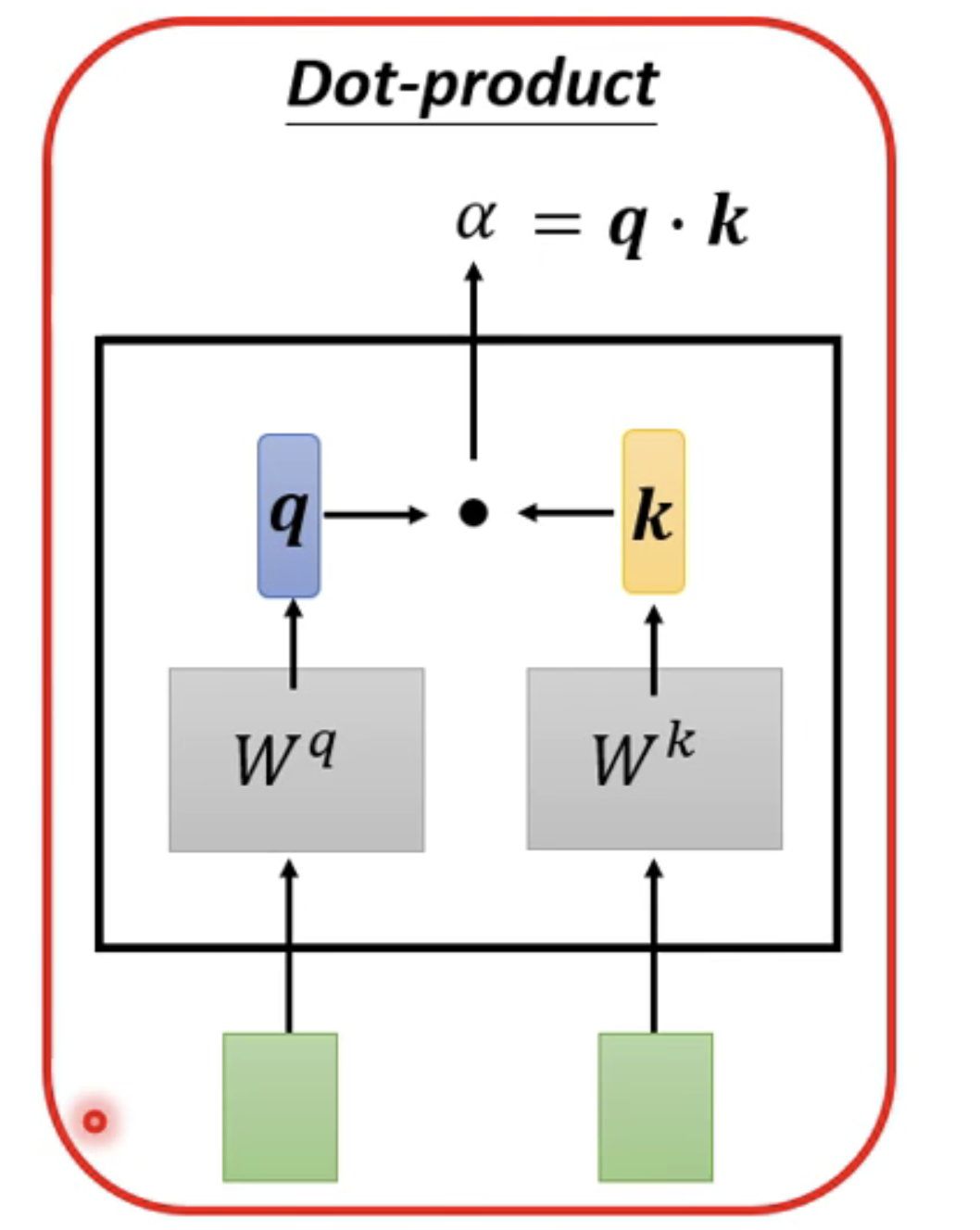
首先,我们拿到绿色的部分 。绿色的部分表示的就是我们输入的向量,a1和a2 ,灰色的Wq和Wk表示我们用a1去和Wq相乘,得到一个向量q,然后使用a2和Wk相乘,得到一个数值k。最后使用q和k进行一个dot product。得到我们的a,a也就是表示两个向量之间的相关联程度。在 transformer当中使用了这样的结构来计算向量之间的相关联性。另外一种方法我们有事也会用到,如下图所示:
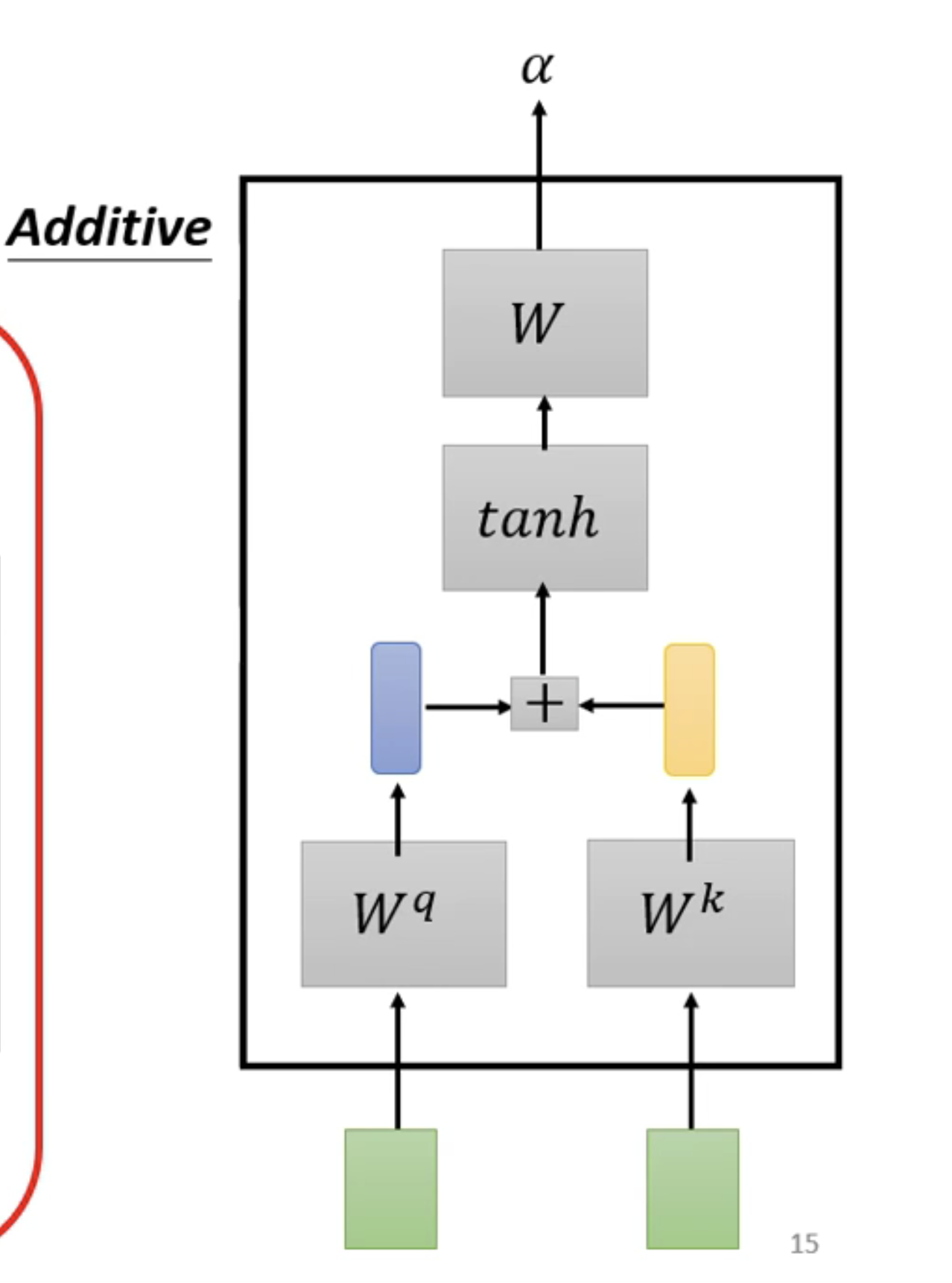
这种机制也是想相乘,后相加,然后使用tanh投射到一个新的函数空间内,再相乘,得到最后的结果。我们对每一个输入的向量都做这样的操作。
当然在得到这个相关程度的结果之后,我们使用softmax计算出一个attention distribution。当然你也可以使用relu来计算,完全看你自己的意愿了。拥有了这个attention distribution我们就知道了哪些向量和我们的a1是最有关系的。
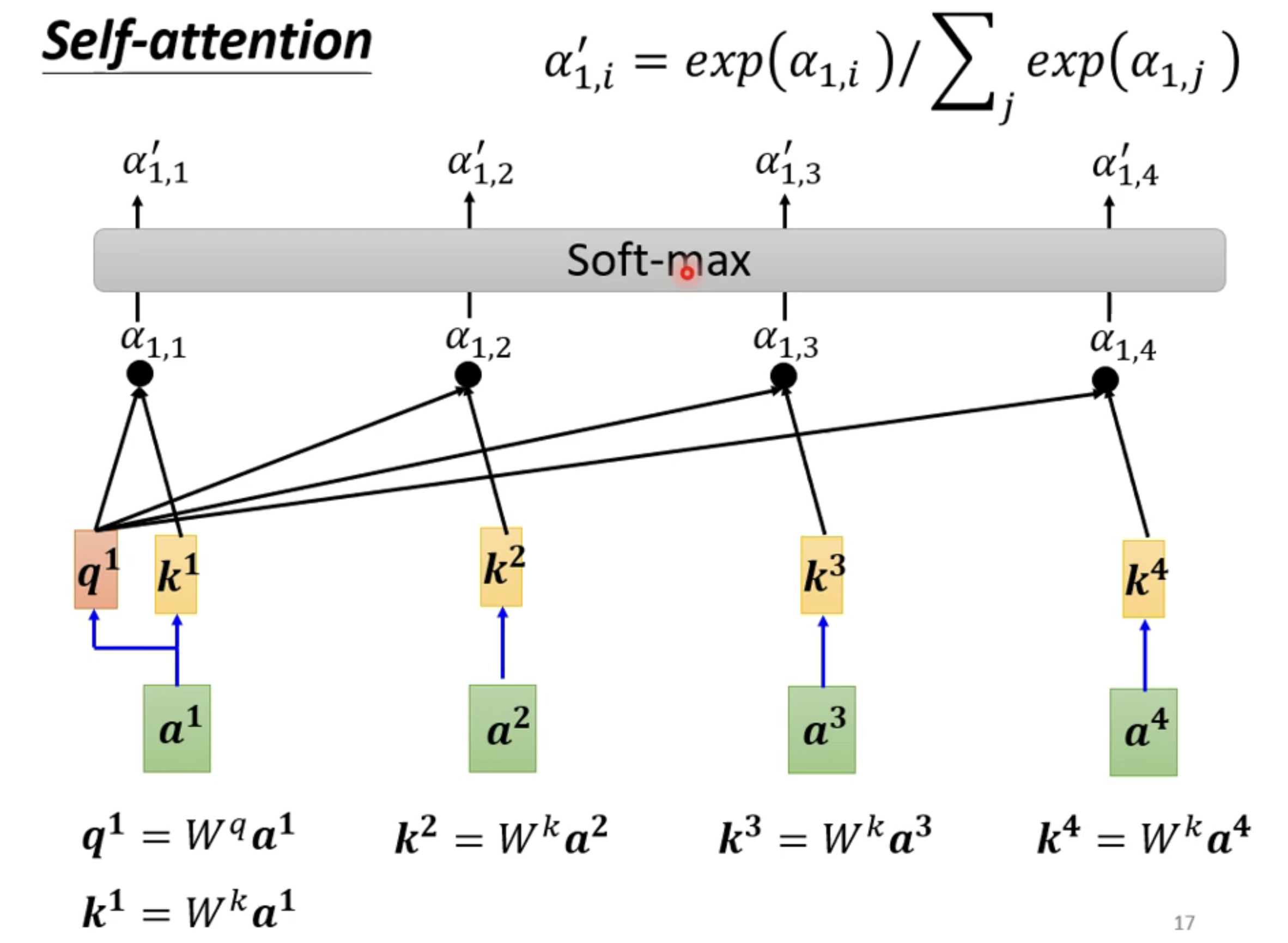
接下来,就来到了我们self-attention当中的一个难点,既然我们目前已经得到了每一个向量和a1之间的相关联程度,那么我们通过这些相关联的程度,再做一次计算。得到一个唯一的数值,再将所有的相关联程度和这个唯一的数值b1相比较,就可以得到最终我们某个向量和某个向量之间的相似程度了。越接近b1的数值,那么我们就越和a1相似。
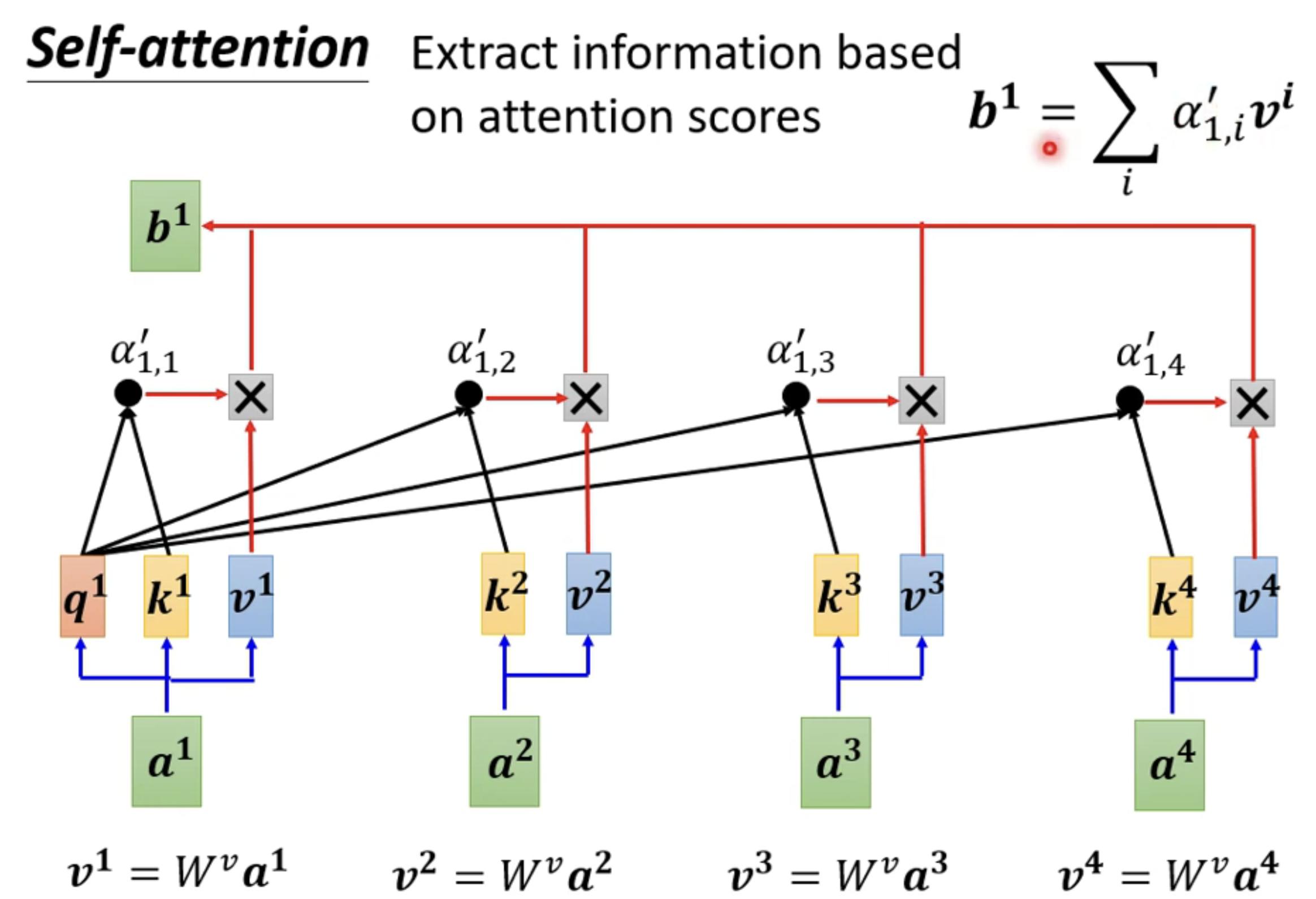
如上图所示,我们使用新的矩阵WV乘上原始矩阵a1,得到一个新的矩阵v1,然后这个矩阵a1再和上main的矩阵相乘,最后每一个向量都做这样的一个操作,就可以得到最后的矩阵,也就是b1了!
二.Multi-Head Self-Attention
在transformer当中,其中应用最广泛的一种self-attention机制,还有一种叫做multi-head self-attention。
这种attention也就是说,对于同一个向量a而言,我们可以具备多组q,k,v来描述a这同一个向量。之前我们仅仅才用了一组q,k,v来描述我们的向量。采用多组向量之后,我们分别对每一组进行计算其b的值,如果有两组,则有两个b的值。如下图所示:
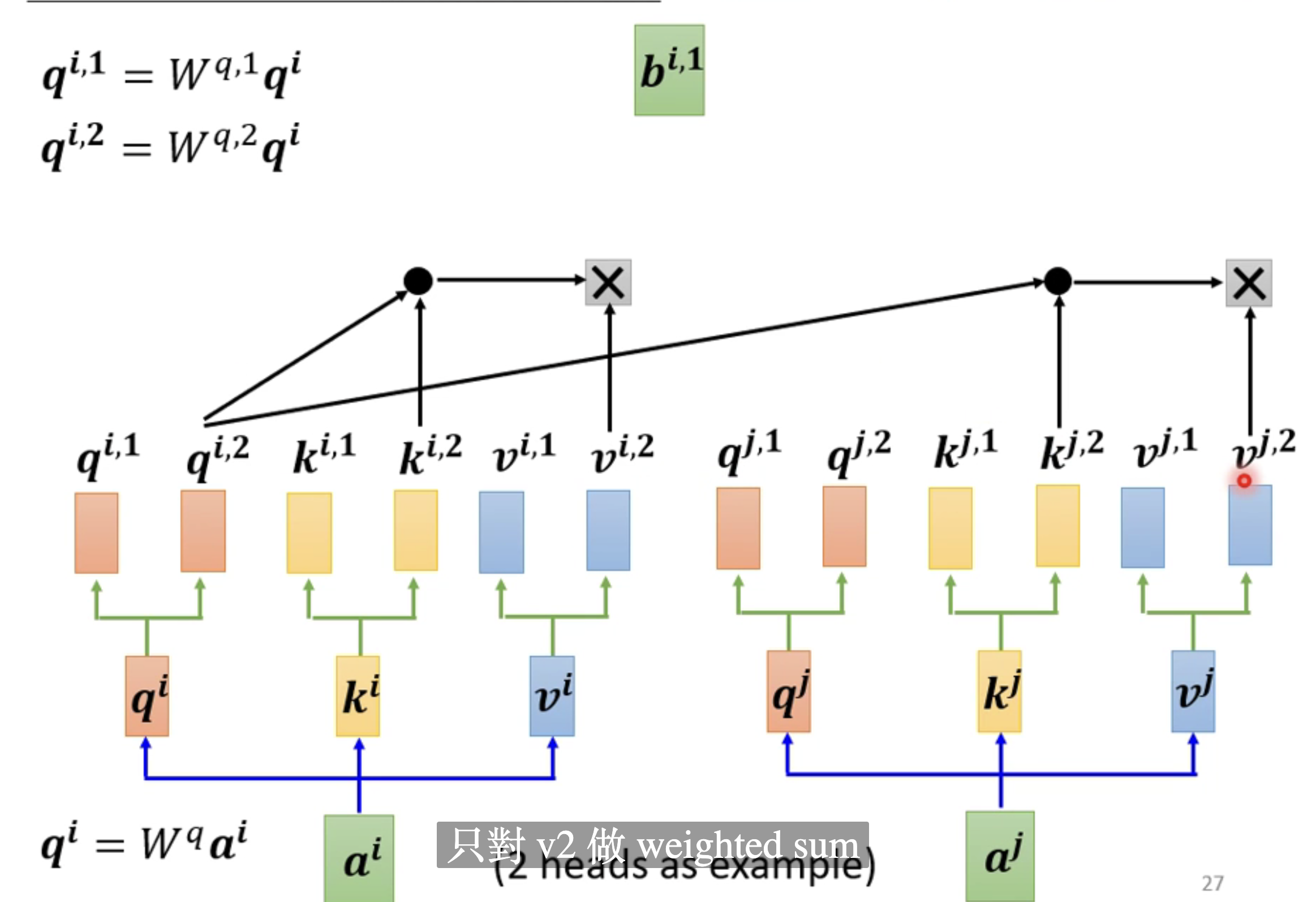
由于这张图我们只对v2做了一个weighted sum,得到一个b1的值。当然我们由于两组这样的值,因此我们会得到两个b值。最后的结果如下所示
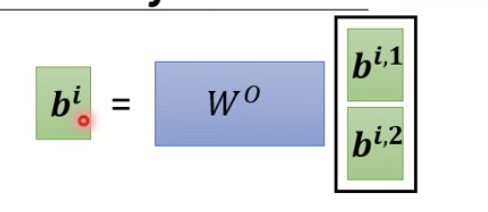 最后我们将两个b的值一起乘以一个矩阵W0,得到最终的bi的值,也就是这个self- attention向量ai的输出。
最后我们将两个b的值一起乘以一个矩阵W0,得到最终的bi的值,也就是这个self- attention向量ai的输出。
三.Positional Encoding
由于我们在训练self attention的时候,实际上对于位置的信息是缺失的,对于lstm或者rnn而言,位置的信息是非常明显的。因此我们可以对每个输入的向量进行positianl encoding,也就是说,在每个输入的向量之间我们可以新建立一个向量,对我们的position进行相应的描述。下面是positianl encoding的一个定义:
也就是说我们可以在插入向量的左边,插入一个有关位置信息的向量ei,插入后的向量如下所示:
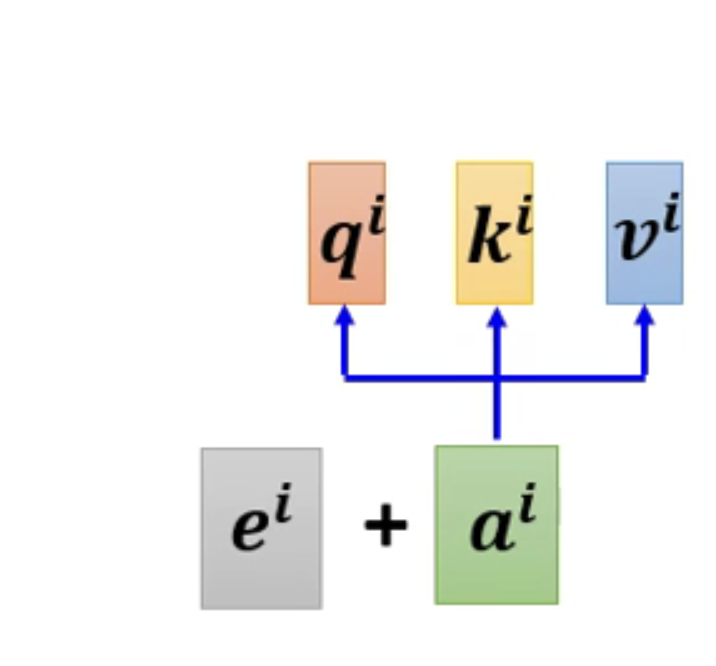 而这个技术经常会在我们的transformer当中所采用到。
而这个技术经常会在我们的transformer当中所采用到。