xxx

操作系统：

1.进程间通信方式

1. 无名管道，pipe，半双工，速度较慢，只能有亲缘关系（父子或兄弟进程）的进程间通信
2. 有名管道，FIFO，破坏性读出，且先进先出，没有亲缘关系的进程
3. 消息队列，消息队列独立于读写进程，要考虑上一次未执行完问题
4. 信号量，不能用于传输复杂消息，只能用于数据同步
5. 共享内存，速度快，需要进行同步
6. socket，UNIX socket 和 web socket

2.线程间通信方式

1. 全局变量
2. 消息机制，postMessge

3.关于线程和进程的异同：

• 从概念上来讲。进程是一个正在运行中的程序，或者说是包含一个程序运行所需所有资源的容器。进程是系统资分配和调度的一个独立单位。线程是进程在某组数据上运行的一个实体，是 cpu 调度和分派的基本单位。是一个比进程更小的独立运行单位。一个进程下的多个线程共享大部分系统资源，拥有自己独立的栈内存。一个进程下的多个线程可以并发的执行。
• 线程比进程更轻量级，调度开销更小。但是线程之间内存会相互影响，一个线程挂掉可能会阻塞掉整个进程。

 4.ftok 函数

• 系统建立IPC通讯 （消息队列、信号量和共享内存） 时必须指定一个ID值。通常情况下，该id值通过ftok函数得到。

5.进程调度算法

1. 先进先出
2. 最短作业优先
3. 时间片轮转法　　 注意时间片选择合适
4. 多级队列 

6.生产者消费者模型

• https://blog.csdn.net/u014174955/article/details/44022391

7.线程安全

• 对于全局以及静态这样的共享内存变量访问需要建立临界保护区，同时尽量避免对临界区访问
• 线程池

8.死锁、互斥锁、读写锁、自旋锁、递归锁、可重入锁

• 何谓自旋锁？它是为实现保护共享资源而提出一种锁机制。其实，自旋锁与互斥锁比较类似，它们都是为了解决对某项资源的互斥使用。无论是互斥锁，还是自旋锁，在任何时刻，最多只能有一个保持者，也就说，在任何时刻最多只能有一个执行单元获得锁。但是两者在调度机制上略有不同。对于互斥锁，如果资源已经被占用，资源申请者只能进入睡眠状态。但是自旋锁不会引起调用者睡眠，如果自旋锁已经被别的执行单元保持，调用者就一直循环在那里看是否该自旋锁的保持者已经释放了锁，"自旋"一词就是因此而得名。

9.乐观锁和悲观锁

• https://blog.csdn.net/L_BestCoder/article/details/79298417

10.页面置换算法

• 最优算法
• FIFO
• 第二次机会算法
• 时钟轮转法
• LRU
• NRU

11.操作系统内存管理

• 分页
• 多级分页
• 块表

mysql

1.事物的四大特性：

• 原子性
• 隔离性
• 持久性
• 一致性

2.mysql 引擎对比，Innodb和MyIASM

• https://www.cnblogs.com/xiaohaillong/p/6079551.html

3.事物隔离级别

• 未提交读：事务中修改，即便没有提交对其他事务也是可见的。事物 B 对表做了修改但未提交，A 第一次读取数据时读取到了修改后的结果，若事务 B 撤销，此时 A 再次读取数据读取到的是修改前的结果。即脏读
• 提交读：未提交的事务对其他事务是不可见的，不会产生脏读。但是若事务 A 多次读取同一数据时事务 B 对该数据做了修改，导致事务 A 多次读取到的结果不一致（行级数据）。即不可重复读
• 可重复读：保证同一事务多次读取同一数据的结果是一致的（行级数据）。但是当事务 A 读取某个范围的数据（表级数据）时另一事务 B 在该范围内插入了新的记录，会产生幻行。即幻读（加表级锁或者 MVCC 可解决幻读问题）
• 串行化：保证不会出现幻读
• 不可重复读侧重于修改，幻读侧重于新增或删除。解决不可重复读的问题只需锁住满足条件的行，解决幻读需要锁表

4.多版本并发控制（MVCC）

• 通过在每行记录后面保持两个隐藏的列来实现的（行的创建版本号列，行的删除版本号列）
• select
  • innodb 只查找版本号早于当前事务版本的数据行。保证读取的数据要么是原本已经存在的，要么是当前事务修改或者插入的
  • 行的删除要么未定义，要么大于当前事务版本号。保证读取的数据在当前事务开始之前未被删除

• insert

  • innodb 为新插入的每一行保存当前事务版本号作为行版本号
• delete
  • innodb 为删除的每一行保持当前事务版本号作为删除版本号
• update
  • innodb 保存当前的事务版本号作为行版本号以及删除版本号

c++

1.容器以及迭代器失效

• 
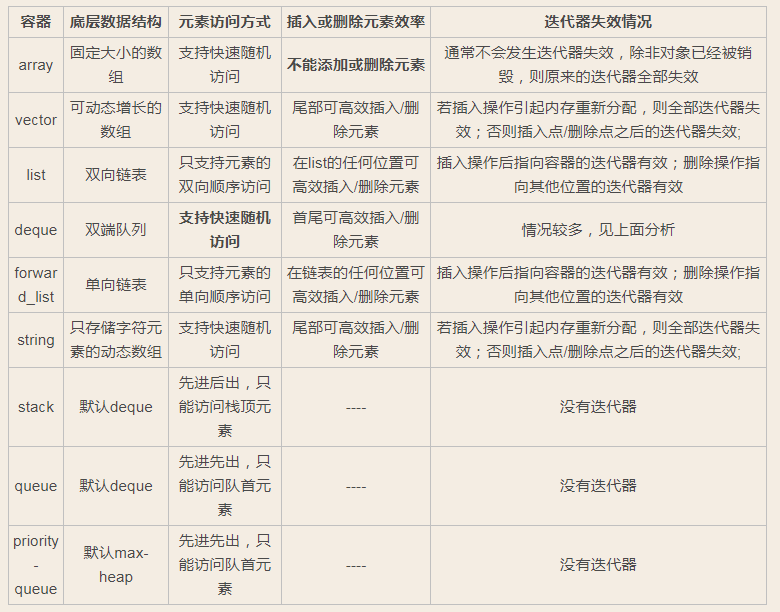
• 关于 dequeue 特别说明：deque则是一种双向开口的连续数据空间。所谓的双向开口，意思是可以在头尾两端分别做元素的插入和删除操作。当然vector也可以在头尾两端进行操作，但是其头部操作效果奇差，所以标准库没有为vector提供push_front或pop_front操作。与vector类似，deque支持元素的快速随机访问。现在问题来了：如果deque以数组来实现，如何做到在头部的常数时间插入？如果是采用链表来实现，又如何做到快速随机访问？deque的内部数据结构到底如何？想必你已经猜到了，要实现如上需求，需要由一段一段的连续空间链接起来的数据结构才能满足。既然deque是由一段一段定长的连续空间所构成，就需要有结构来管理这些连续空间。deque采用一块map（非STL中的map）作为主控，map是一块小的连续空间，其中每个元素都是指针，指向一块较大的线性连续空间，称为缓冲区。而缓冲区才是存储deque元素的空间主体
• • 在deque容器首部或者尾部插入元素不会使得任何迭代器失效。
  • 在其首部或尾部删除元素则只会使指向被删除元素的迭代器失效。
  • 在deque容器的任何其他位置的插入和删除操作将使指向该容器元素的所有迭代器失效

 2.重载、重写以及隐藏的区别

• 重载是一种静态多态行为。对于多个同名但形参个数或者形参类型不同的函数，在调用时会静态的选择调用实参对应的函数
• 重写是指在子类中覆盖继承自父类中的方法
• 隐藏是指父类中的方法被子类继承了，但由于该方法被定义成了private，在子类中不能访问

3.返回值不同能否构成重载

• 不能

4.strcpy 和 memcpy 是不是原子的

• 是

5.c++调用成员函数的过程

• 假设我们调用 p_>mem()（或者 obj.mem()）:

  首先确定 p(或 obj) 的静态类型。

  在 p(或 obj) 的静态类型对应的类中查找 mem。如果找不到，则依次在直接基类中不断查找直至达到继承链的顶端。如果仍然找不到则编译器报错

  一旦找到了 mem，就进行常规的类型检查以确认对于当前找到的 mem，本次调用是否合法。

  假设调用合法，则编译器将根据调用的是否是虚函数而产生不同的代码：

  ——如果 mem 是虚函数且我们是通过引用或指针进行的调用，则编译器产生的代码将在运行时确定到底运行哪个版本，依据是对象的动态类型

  ——反之，如果 mem 不是虚函数或者我们是通过对象(非指针或引用)进行的调用，则编译器将产生一个常规函数调用

6.如何构建子类的虚函数表

• https://www.cnblogs.com/malecrab/p/5572730.html
• 分三步，首先拷贝一份父类的虚函数表，然后将子类中重写的虚函数对应的指针替换原本拷贝的虚函数表中对应的父类虚函数指针。最后在后面追加自己的虚函数指针
• 通过上面的描述可以发现父类和子类中对应的虚函数在各自的虚函数表中的偏移位是一样的

7.执行虚函数的过程

• 按照5中步骤到确认是多态调用后。先从对象的静态类型中获取所调用的虚函数指针偏移位。在6中我们知道了父类和子类中对应虚函数指针在各自虚函数表中的偏移位是相同的。然后在执行调用虚函数时确认了执行调用虚函数的对象具体类型，拿着我们前面得到的偏移指针就可以到对应的虚函数表中找到需要调用的虚函数指针。然后根据指针进行调用即可

8.优先队列的数据结构是什么？堆

算法

计算机网络

1.url、uri 和 urn 

2.http 事务

• 由一个http请求和其响应组成

3.常见的 http 请求方法

• 
• Trace 获取服务端实际接搜到的 request，因为客户端和服务端中间可能还存在其他的网络实体（代理等）在转发 request 的时候会做一些改变。导致 server 接收到的 request 和 client 发送的不一致。主要用于调试。
• 安全方法的概念，幂等的概念（GET，HEAD）
• 扩展方法...

4.常见的 http 状态码

• 

5.http 报文

• 

6.在浏览器中访问一条 url 的步骤

• 

7.常见 http 部首

• 

8.http 事务时延的主要原因

• 对于最近没有访问的 uri 主机，需要访问 dns server 进行解析。要花费数十秒
• 对于短连接，每个 http 事务都要建立一次 http 连接，其本质是建立一次 tcp 连接，这个值通常是数秒钟。但是对于串行的 http 事务来说，这些 http 事务的时延是叠加的。而打开一个网页时可能会有多个 http 事务，那么建立连接的时延可能会迅速叠加达到数分钟
• 流量在网络中传输需要时间
• 建立连接后服务端处理用户的请求
• 服务端处理完后返回 http 响应

9.tcp 时延

• tcp 连接建立握手
• tcp 慢启动拥塞控制
• Nagel 算法。为避免发送只携带很少数据的 tcp 分组，Nagel 算法试图在发送一个分组前将大量的 tcp 数组绑到一起发送。当使用 pipe 的时候这个问题会比较突出
• 延时确认算法。由于网络本身的不可靠性，每个 tcp 段都会有一个序列号和一个完整性校验和。当接收端收到完好的段时，都会像发送方发一个很小的确认分组。若发送者在规定时间内没有收到确认分组就认为之前发送的那个 tcp 段被破坏了并重发。由于确认报文很小，可以被通方向上的 tcp 段捎带。延迟确认算法维护了一个特定的窗口时间（100~200ms）用于寻找能捎带确认段的 tcp 段。若规定时间内没有输出数据分组，则将确认信息单独放到分组中发送。 2
time_wait（2MSL，通常为 2 min）。time_wait 的作用：
• 维护 2MSL 时间的最近关闭的 host，以避免短时间内创建相同的连接
• 确保被动关闭连接端收到了主动关闭端的最后一个ack
• 防止“已经失效的连接请求报文段”出现在本连接中。客户端发送完最后一个确认报文后，在这个2MSL时间中，就可以使本连接持续的时间内所产生的所有报文段都从网络中消失。这样新的连接中不会出现旧连接的请求报文（1和3都是针对避免收到逗留在网络中的失效报文影响）

11.关于 time_wait 累积和端口耗尽

• 在只有一个 server 和一个 client 的情况下，构建 tcp 连接的 4 元组 <服务端ip，服务端port，客户端ip，客户端port> 其中三个都是固定的——只有客户端port可以随意改变。客户端每次连接到服务器时都会获得一个新的源端口（客户端port）以保证 tcp 连接的唯一性。由于可用的源端口有限，且在 2MSL 中无法重复使用。若建立 tcp 连接的频率太高就会产生源端口耗尽问题。比如有 60000 个可用端口，2MSL = 120s，则建立连接的频率不能高于 60000 / 120 = 500 次/s
• 解决方案，修改 /etc/sysctl.conf 配置文件，加快 time_wait 状态的回收

12.关于 close_wait 状态

• 在被动关闭连接端接收到主动关闭连接端的 FIN，但是自己还没发送 FIN 的这段时间的状态称为 CLOSE_WAIT，正常情况下，这个状态的持续时间很短。但当被动关闭端在半连接状态下进行读写操作时这个状态可能会持续比较长的时间
• 解决方案，这个问题通常是代码的问题（对方关闭了连接，而己方还在进行读写操作）。

13.提高 http 的连接性能

• 并行连接。并发的发起多个 http 事务。因为一个网页中可能有多个 http 事务，而串行 http 事务会叠加相邻的两个 http 事务之间的时延。并发 http 事务能有效减少这部分时延。需要注意的是并行发起 http 请求不一定就比串行快。主要原因有三：
  • 其一是浏览器连接都因特网的带宽是有限的（28.8kbps），在连接一个速度比较快的服务器时带宽很容易达到这个瓶颈，此时使用并发连接反而会引起多个连接之间相互挤占带宽的问题而影响速度
  • 其二是发起大量 http 连接需要消耗大量内存资源，可能会导致客户端发生故障
  • 其三是可能会对服务器造成太大压力，引起服务端性能下降。如某个网页有上百个内嵌资源对象，若有1000个用户同时访问该网站，则服务器要处理 100000 个连接
• 持久连接。非持久连接每执行完一个 http 事务就关闭连接。持久连接即执行完一个 http 事务后不关闭该连接。由于站点本地性（一个网页中的大部分内嵌资源都是从同一个站点获取的）。通过持久连接复用前面开启的连接，避免建立 tcp 连接以及拥塞控制慢启动部分导致的时延。http1.1版本开始默认建立持久连接
• 管道连接。对于持久连接可以选择管道化连接，即缓存一个任务队列，当上一个请求发送后紧接着下一个请求流向服务端。需要注意的是：
  • 只有持久连接可以管道化
  • 对于断开连接后未完成发送的请求，需要重新发送这些请求
  • 不能对非幂等的请求（如：post）使用管道连接。因为非幂等的请求无法被安全的重试

14.对比 http2.0 和 http1.0

• http2.0 采用二进制格式而非文本格式。相对文本格式来说，二进制格式解析起来更快，也更不容易出错
• http2.0 是多路复用的（链接共享）。个request对应一个stream并分配一个id，这样一个连接上可以有多个stream，每个stream的frame可以随机的混杂在一起，接收方可以根据stream id将frame再归属到各自不同的request里面。
• header 压缩
• http2.0 让服务器可以将响应主动“推送”到客户端缓存中

14.IP分组以及tcp段

15、dns解析

https://www.zhihu.com/question/23042131

16、nginx

缺点：

1、支持的协议范围小，只支持 http, https, email协议

2、对后端服务器的健康检查，只支持通过端口来检测，不支持通过url来检测。不支持Session的直接保持，但能通过ip_hash来解决

17、udp协议

头部报文结构

udp头部长度为8字节，包含16位源端口，16位目标端口，16位长度，16位校验和

18、最大udp报文长度多少

由17中udp头部报文结构长度位16位可知，最大udp报文长度位65535字节（包括udp首部）。另外，如果考虑不要ip分片（ip协议不可靠，如果分片重组udp报文会比较麻烦）的话则最大报文长度不能超过1500（以太帧的MTU）-20（最小的ip首部长度）=1480（udp的MTU），再去除udp首部，即传输的最大应用数据长度不能超过1472字节。但在网络编程中，Internet中的路由器可能有设置成不同的值(小于默认值)，Internet上的标准MTU值为576，所以Internet的UDP编程时数据长度最好在576－20－8＝548字节以内。

 手撸代码

1.LRU算法

#include <iostream>
#include <unordered_map>
#include <list>
using namespace std;

// 新数据插入链表头部
// 每当缓存命中（即缓存数据被访问），则将数据移到链表头部
// 当链表满的时候，将链表尾部的数据丢弃

const int MAXN = 10;

class lru {
public:
  int num = 0;
  unordered_map<int, int> mp;
  list<int> li;

  int getValue(int key) {
    if(!mp[key]) {//key不在缓存中
      if(this->num == MAXN) {//缓存满了，丢弃list最后一个元素
        this->delet(this->li.back());
      }
      this->insert(key);//插入新值
    } else {//命中缓存，将key移到头部
      this->delet(key);
      this->insert(key);
    }
  }

  int insert(int key) {
    li.push_front(key);
    mp[key] = 1;
    ++this->num;
  }

  int delet(int key) {
    li.remove(key);
    mp[key] = 0;
    --this->num;
  }

  void echo(void) {
    for(auto it = this->li.begin(); it != li.end(); ++it) {
      cout << *it << " ";
    }
    cout << endl;
  }
};

int main(void) {

}

2.堆排 不稳定

#include <iostream>
using namespace std;

//维护以 head 为顶点的二叉树为大根堆
void done(int *a, int head, int n) {
    while((head << 1) + 1 < n) {
        int cnt = (head << 1) + 1;
        if(cnt + 1 < n && a[cnt] < a[cnt + 1]) {
            ++cnt;
        }
        if(a[head] < a[cnt]) {
            a[head] ^= a[cnt];
            a[cnt] ^= a[head];
            a[head] ^= a[cnt];
            head = cnt;
        } else break;
    }
}

//对 a 升序排序
void heap_sort(int *a, int size) {
    //先初始化一个大根堆，然后依次将堆顶元素加入数组末尾同时维护大根堆
    for(int i = (size >> 1) - 1; i >= 0; --i) {
        done(a, i, size);
    }

    //注意这里 i < size - 1 而非 i < size，不然会出现 a[0] ^= a[0] 的情况，最后一个元素是自然确定的，不需要再交换
    for(int i = 0; i < size - 1; ++i) {
        a[0] ^= a[size - i - 1];
        a[size - i - 1] ^= a[0];
        a[0] ^= a[size - i - 1];

        done(a, 0, size - i - 1);
    }
}

int main(void) {
    int n;
    const int MAXN = 1e3;
    int a[MAXN];

    cin >> n;
    for(int i = 0; i < n; ++i) {
        cin >> a[i];
    }

    heap_sort(a, n);

    for(int i = 0; i < n; ++i) {
        cout << a[i] << " ";
    }
    cout << endl;

    return 0;
}

3.归并排序 稳定

//归并排序
#include <iostream>
using namespace std;

void print(int *a, int size) {
    for(int i = 0; i < size; ++i) {
        cout << a[i] << " ";
    }
    cout << endl;
}

void merge_sort(int *a, int *t, int l, int r) {
    if(r - l > 1) {
        int mid = (l + r) >> 1;

        merge_sort(a, t, l, mid);//[l,mid)
        merge_sort(a, t, mid, r);//[mid, r)

        int i = l, p = l, q = mid;

        //合并到临时数组
        while(p < mid || q < r) {
            if(q >= r || (p < mid && a[q] > a[p])) {
                t[i++] = a[p++];
            } else t[i++] = a[q++];
        }

        //将排好序的元素放回到原来区间
        for(int j = l; j < r; ++j) {
            a[j] = t[j];
        }
    }
}

int main(int argc, char const *argv[])
{
    const int MAXN = 1e3;
    int n;
    int a[MAXN];
    int t[MAXN];

    cin >> n;
    for(int i = 0; i < n; ++i) {
        cin >> a[i];
    }

    merge_sort(a, t, 0, n);

    print(a, n);

    return 0;
}

4.快排 不稳定

//快排
#include <iostream>
using namespace std;

void print(int *a, int size) {
    for(int i = 0; i < size; ++i) {
        cout << a[i] << " ";
    }
    cout << endl;
}

//对 [l,r) 区间进行快排
void fast_sort(int *a, int l, int r) {
    if(l < r - 1) {
        int i = l, j = r - 1, key = a[l];
        while(i < j) {
            for(; i < j && key <= a[j]; --j);
            a[i] = a[j];
            for(; i < j && key >= a[i]; ++i);
            a[j] = a[i];
        }
        a[i] = key;

        fast_sort(a, l, i);//[l, i)
        fast_sort(a, i + 1, r);//[i + 1, r)
    }
}

int main(void) {
    const int MAXN = 1e3;
    int a[MAXN];
    int n;

    cin >> n;
    for(int i = 0; i < n; ++i) {
        cin >> a[i];
    }

    fast_sort(a, 0, n);

    print(a, n);

    return 0;
}

5.实现 hash_map

6.重构二叉树

7.我们有n个蛋，k层楼，假设蛋从第m层楼及以上往下扔会碎，现在要找到m，问在最坏的情况下至少需要试出多少次才能知道m。w(n,k)表示次数。写出状态转移方程w(n,k)。

8、手写单例模式，并分析一下双重校验锁的作用？