省选前模板总结

DATA STRUCTURE

1.数据结构

1.1字符串哈希

为后缀计算一个哈希值，满足(H(i)=H(i+1)x+s[i])（其中(0 leq i < n, H(n) = 0)），例如

[H(4)=s[4] ]

[H(3)=s[4]x+s[3] ]

一般地，(H(i)=s[n-1]x^{n-1-i}+s[n-2]x^{n-2-i}+...+s[i+1]x+s[i])
对于一段长度为L的子串s[i]~s[i+L-1]，定义他的哈希值(Hash(i, L) = H(i)-H(i+L)x^L)。
预处理H和(x^L)。注意到hash值很大，我们把他存在unsigned long long中，这样就实现了自然溢出，可以大大减小常数。

1.2树状数组

1.2.1普通树状数组

树状数组好写好调，能用树状数组的时候尽量要使用。
树状数组从1开始。

int lowbit(int x) { return x & -x; }
int sum(int x) {
  int ans = 0;
  while (x) {
    ans += bit[x];
    x -= lowbit(x);
  }
  return ans;
}
void add(int i, int x) {
  while (i <= n) {
    bit[i] += x;
    i += lowbit(i);
  }
}

1.2.2支援区间修改的树状数组

假设对于区间([a, b])增加k，令g[i]为加了k以后的数组。

[g[i] = s[i] (i < a) ]

[g[i] = s[i] + i*k - k(a-1) (i >= a 且 i <= b) ]

[g[i] = s[i] + b*k - k(a-1) (i > b) ]

所以我们开设两个树状数组。

1.2.3二维树状数组

直接扩展就可以了。非常的直观和显然。

//bzoj3132
void change(int id, int x, int y, int val) {
  for (int i = x; i <= n; i += i & -i) {
    for (int j = y; j <= m; j += j & -j) {
      c[id][i][j] += val;
    }
  }
}
int qu(int id, int x, int y) {
  int ans = 0;
  for (int i = x; i > 0; i -= i & -i) {
    for (int j = y; j > 0; j -= j & -j) {
      ans += c[id][i][j];
    }
  }
  return ans;
}

1.3线段树

1.3.1普通线段树

这个线段树版本来自bzoj1798，代表了一种最基础的线段树类型，支持区间修改，多重标记下传等等操作。

//bzoj1798
void build(int k, int l, int r) {
  t[k].l = l;
  t[k].r = r;
  if (r == l) {
    t[k].tag = 1;
    t[k].add = 0;
    scanf("%lld", &t[k].sum);
    t[k].sum %= p;
    return;
  }
  int mid = (l + r) >> 1;
  build(k << 1, l, mid);
  build(k << 1 | 1, mid + 1, r);
  t[k].sum = (t[k << 1].sum + t[k << 1 | 1].sum) % p;
  t[k].add = 0;
  t[k].tag = 1;
}
void pushdown(int k) {
  if (t[k].add == 0 && t[k].tag == 1)
    return;
  ll ad = t[k].add, tag = t[k].tag;
  ad %= p, tag %= p;
  int l = t[k].l, r = t[k].r, mid = (l + r) >> 1;
  t[k << 1].tag = (t[k << 1].tag * tag) % p;
  t[k << 1].add = ((t[k << 1].add * tag) % p + ad) % p;
  t[k << 1].sum = (((t[k << 1].sum * tag) % p + (ad * (mid - l + 1) % p)%p)%p) % p;
  t[k << 1 | 1].tag = (t[k << 1 | 1].tag * tag) % p;
  t[k << 1 | 1].add = ((t[k << 1 | 1].add * tag) % p + ad) % p;
  t[k << 1 | 1].sum = (((t[k << 1|1].sum * tag) % p + (ad * (r-mid) % p)%p)%p) % p;
  t[k].add = 0;
  t[k].tag = 1;
  return;
}
void update(int k) { t[k].sum = (t[k << 1].sum%p + t[k << 1 | 1].sum%p) % p; }
void add(int k, int x, int y, ll val) {
  int l = t[k].l, r = t[k].r, mid = (l + r) >> 1;
  if (x <= l && r <= y) {
    t[k].add = (t[k].add + val) % p;
    t[k].sum = (t[k].sum + (val * (r - l + 1) % p) % p) % p;
    return;
  }
  pushdown(k);
  if (x <= mid)
    add(k << 1, x, y, val);
  if (y > mid)
    add(k << 1 | 1, x, y, val);
  update(k);
}
void mul(int k, int x, int y, ll val) {
  int l = t[k].l, r = t[k].r, mid = (l + r) >> 1;
  if (x <= l && r <= y) {
    t[k].add = (t[k].add * val) % p;
    t[k].tag = (t[k].tag * val) % p;
    t[k].sum = (t[k].sum * val) % p;
    return;
  }
  pushdown(k);
  if (x <= mid)
    mul(k << 1, x, y, val);
  if (y > mid)
    mul(k << 1 | 1, x, y, val);
  update(k);
}
ll query(int k, int x, int y) {
  int l = t[k].l, r = t[k].r, mid = (l + r) >> 1;
  if (x <= l && r <= y) {
    return t[k].sum%p;
  }
  pushdown(k);
  ll ans = 0;
  if (x <= mid)
    ans = (ans + query(k << 1, x, y)) % p;
  if (y > mid)
    ans = (ans + query(k << 1 | 1, x, y)) % p;
  update(k);
  return ans%p;
}

1.3.2可持久化线段树

一种可持久化数据结构。
继承一样的节点，只是把修改的重新链接，节省空间。
容易爆空间。
经常与权值线段树和二分答案结合。

int rt[maxn], lc[maxm], rc[maxm], sum[maxm];
void update(int l, int r, int x, int &y, int v) {
  y = ++sz;
  sum[y] = sum[x] + 1;
  if (l == r)
    return;
  lc[y] = lc[x];
  rc[y] = rc[x];
  int mid = (l + r) >> 1;
  if (v <= mid)
    update(l, mid, lc[x], lc[y], v);
  else
    update(mid + 1, r, rc[x], rc[y], v);
}

1.3.3标记永久化

一种奇怪的姿势，又称李超线段树。
给节点打下的标记不进行下传，而是仅仅在需要的时候进行下传，这就是所谓永久化标记。

struct line {
  double k, b;
  int id;
  double getf(int x) { return k * x + b; };
};
bool cmp(line a, line b, int x) {
  if (!a.id)
    return 1;
  return a.getf(x) != b.getf(x) ? a.getf(x) < b.getf(x) : a.id < b.id;
}
const int maxn = 50010;
line t[maxn << 2];
line query(int k, int l, int r, int x) {
  if (l == r)
    return t[k];
  int mid = (l + r) >> 1;
  line tmp;
  if (x <= mid)
    tmp = query(k << 1, l, mid, x);
  else
    tmp = query(k << 1 | 1, mid + 1, r, x);
  return cmp(t[k], tmp, x) ? tmp : t[k];
}
void insert(int k, int l, int r, line x) {
  if (!t[k].id)
    t[k] = x;
  if (cmp(t[k], x, l))
    std::swap(t[k], x);
  if (l == r || t[k].k == x.k)
    return;
  int mid = (l + r) >> 1;
  double X = (t[k].b - x.b) / (x.k - t[k].k);
  if (X < l || X > r)
    return;
  if (X <= mid)
    insert(k << 1, l, mid, t[k]), t[k] = x;
  else
    insert(k << 1 | 1, mid + 1, r, x);
}
void Insert(int k, int l, int r, int x, int y, line v) {
  if (x <= l && r <= y) {
    insert(k, l, r, v);
    return;
  }
  int mid = (l + r) >> 1;
  if (x <= mid)
    Insert(k << 1, l, mid, x, y, v);
  if (y > mid)
    Insert(k << 1 | 1, mid + 1, r, x, y, v);
}

1.4 平衡树

1.4.1 Splay伸展树

一种最为常用的BBST。

int ch[maxn][2], fa[maxn];
int size[maxn], data[maxn], sum[maxn], la[maxn], ra[maxn], ma[maxn], cov[maxn],
    a[maxn];
bool rev[maxn];
int n, m, sz, rt;
std::stack<int> st;
void update(int x) {
  if (!x)
    return;
  la[x] = std::max(la[l(x)], sum[l(x)] + data[x] + std::max(0, la[r(x)]));
  ra[x] = std::max(ra[r(x)], sum[r(x)] + data[x] + std::max(0, ra[l(x)]));
  ma[x] = std::max(std::max(ma[l(x)], ma[r(x)]),
                   data[x] + std::max(0, ra[l(x)]) + std::max(0, la[r(x)]));
  sum[x] = sum[l(x)] + sum[r(x)] + data[x];
  size[x] = size[l(x)] + size[r(x)] + 1;
}
void reverse(int x) {
  if (!x)
    return;
  std::swap(ch[x][0], ch[x][1]);
  std::swap(la[x], ra[x]);
  rev[x] ^= 1;
}
void recover(int x, int v) {
  if (!x)
    return;
  data[x] = cov[x] = v;
  sum[x] = size[x] * v;
  la[x] = ra[x] = ma[x] = std::max(v, sum[x]);
}
void pushdown(int x) {
  if (!x)
    return;
  if (rev[x]) {
    reverse(ch[x][0]);
    reverse(ch[x][1]);
    rev[x] = 0;
  }
  if (cov[x] != -inf) {
    recover(ch[x][0], cov[x]);
    recover(ch[x][1], cov[x]);
    cov[x] = -inf;
  }
}
void zig(int x) {
  int y = fa[x], z = fa[y], l = (ch[y][1] == x), r = l ^ 1;
  fa[ch[y][l] = ch[x][r]] = y;
  fa[ch[x][r] = y] = x;
  fa[x] = z;
  if (z)
    ch[z][ch[z][1] == y] = x;
  update(y);
  update(x);
}
void splay(int x, int aim = 0) {
  for (int y; (y = fa[x]) != aim; zig(x))
    if (fa[y] != aim)
      zig((ch[fa[y]][0] == y) == (ch[y][0] == x) ? y : x);
  if (aim == 0)
    rt = x;
  update(x);
}
int pick() {
  if (!st.empty()) {
    int x = st.top();
    st.pop();
    return x;
  } else
    return ++sz;
}
int setup(int x) {
  int t = pick();
  data[t] = a[x];
  cov[t] = -inf;
  rev[t] = false;
  sum[t] = 0;
  la[t] = ra[t] = ma[t] = -inf;
  size[t] = 1;
  return t;
}
int build(int l, int r) {
  int mid = (l + r) >> 1, left = 0, right = 0;
  if (l < mid)
    left = build(l, mid - 1);
  int t = setup(mid);
  if (r > mid)
    right = build(mid + 1, r);
  if (left) {
    ch[t][0] = left, fa[left] = t;
  } else
    size[ch[t][0]] = 0;
  if (right) {
    ch[t][1] = right, fa[right] = t;
  } else
    size[ch[t][1]] = 0;
  update(t);
  return t;
}
int find(int k) {
  int x = rt, ans;
  while (x) {
    pushdown(x);
    if (k == size[ch[x][0]] + 1)
      return ans = x;
    else if (k > size[ch[x][0]] + 1) {
      k -= size[ch[x][0]] + 1;
      x = ch[x][1];
    } else
      x = ch[x][0];
  }
  return -1;
}
void del(int &x) {
  if (!x)
    return;
  st.push(x);
  fa[x] = 0;
  del(ch[x][0]);
  del(ch[x][1]);
  la[x] = ma[x] = ra[x] = -inf;
  x = 0;
}
void print(int x) {
  if (!x)
    return;
  if (ch[x][0])
    print(ch[x][0]);
  std::cout << data[x] << ' ';
  if (ch[x][1])
    print(ch[x][1]);
}

1.5树套树

1.5.1 线段树套splay

您需要写一种数据结构（可参考题目标题），来维护一个有序数列，其中需要提供以下操作：

1. 查询k在区间内的排名
2. 查询区间内排名为k的值
3. 修改某一位值上的数值
4. 查询k在区间内的前驱(前驱定义为小于x，且最大的数)
5. 查询k在区间内的后继(后继定义为大于x，且最小的数)

#include <algorithm>
#include <cctype>
#include <cstdio>
using namespace std;
const int maxn = 4e6 + 5;
const int inf = 1e9;
int ans, n, m, opt, l, r, k, pos, sz, Max;
int a[maxn], fa[maxn], ch[maxn][2], size[maxn], cnt[maxn], data[maxn], rt[maxn];
inline int read() {
  int x = 0, f = 1;
  char ch = getchar();
  while (!isdigit(ch)) {
    if (ch == '-')
      f = -1;
    ch = getchar();
  }
  while (isdigit(ch)) {
    x = x * 10 + ch - '0';
    ch = getchar();
  }
  return x * f;
}
struct Splay {
  void clear(int x) {
    fa[x] = ch[x][0] = ch[x][1] = size[x] = cnt[x] = data[x] = 0;
  }
  void update(int x) {
    if (x) {
      size[x] = cnt[x];
      if (ch[x][0])
        size[x] += size[ch[x][0]];
      if (ch[x][1])
        size[x] += size[ch[x][1]];
    }
  }
  void zig(int x) {
    int y = fa[x], z = fa[y], l = (ch[y][1] == x), r = l ^ 1;
    fa[ch[y][l] = ch[x][r]] = y;
    fa[ch[x][r] = y] = x;
    fa[x] = z;
    if (z)
      ch[z][ch[z][1] == y] = x;
    update(y);
    update(x);
  }
  void splay(int i, int x, int aim = 0) {
    for (int y; (y = fa[x]) != aim; zig(x))
      if (fa[y] != aim)
        zig((ch[fa[y]][0] == y) == (ch[y][0] == x) ? y : x);
    if (aim == 0)
      rt[i] = x;
  }
  void insert(int i, int v) {
    int x = rt[i], y = 0;
    if (x == 0) {
      rt[i] = x = ++sz;
      fa[x] = ch[x][0] = ch[x][1] = 0;
      size[x] = cnt[x] = 1;
      data[x] = v;
      return;
    }
    while (1) {
      if (data[x] == v) {
        cnt[x]++;
        update(y);
        splay(i, x);
        return;
      }
      y = x;
      x = ch[x][v > data[x]];
      if (x == 0) {
        ++sz;
        fa[sz] = y;
        ch[sz][0] = ch[sz][1] = 0;
        size[sz] = cnt[sz] = 1;
        data[sz] = v;
        ch[y][v > data[y]] = sz;
        update(y);
        splay(i, sz);
        rt[i] = sz;
        return;
      }
    }
  }
  void find(int i, int v) {
    int x = rt[i];
    while (1) {
      if (data[x] == v) {
        splay(i, x);
        return;
      } else
        x = ch[x][v > data[x]];
    }
  }
  int pre(int i) {
    int x = ch[rt[i]][0];
    while (ch[x][1])
      x = ch[x][1];
    return x;
  }
  int succ(int i) {
    int x = ch[rt[i]][1];
    while (ch[x][0])
      x = ch[x][0];
    return x;
  }
  void del(int i) {
    int x = rt[i];
    if (cnt[x] > 1) {
      cnt[x]--;
      return;
    }
    if (!ch[x][0] && !ch[x][1]) {
      clear(rt[i]);
      rt[i] = 0;
      return;
    }
    if (!ch[x][0]) {
      int oldroot = x;
      rt[i] = ch[x][1];
      fa[rt[i]] = 0;
      clear(oldroot);
      return;
    }
    if (!ch[x][1]) {
      int oldroot = x;
      rt[i] = ch[x][0];
      fa[rt[i]] = 0;
      clear(oldroot);
      return;
    }
    int y = pre(i), oldroot = x;
    splay(i, y);
    rt[i] = y;
    ch[rt[i]][1] = ch[oldroot][1];
    fa[ch[oldroot][1]] = rt[i];
    clear(oldroot);
    update(rt[i]);
    return;
  }
  int rank(int i, int v) {
    int x = rt[i], ans = 0;
    while (1) {
      if (!x)
        return ans;
      if (data[x] == v)
        return ((ch[x][0]) ? size[ch[x][0]] : 0) + ans;
      else if (data[x] < v) {
        ans += ((ch[x][0]) ? size[ch[x][0]] : 0) + cnt[x];
        x = ch[x][1];
      } else if (data[x] > v) {
        x = ch[x][0];
      }
    }
  }
  int find_pre(int i, int v) {
    int x = rt[i];
    while (x) {
      if (data[x] < v) {
        if (ans < data[x])
          ans = data[x];
        x = ch[x][1];
      } else
        x = ch[x][0];
    }
    return ans;
  }
  int find_succ(int i, int v) {
    int x = rt[i];
    while (x) {
      if (v < data[x]) {
        if (ans > data[x])
          ans = data[x];
        x = ch[x][0];
      } else
        x = ch[x][1];
    }
    return ans;
  }
} sp;
void insert(int k, int l, int r, int x, int v) {
  int mid = (l + r) >> 1;
  sp.insert(k, v);
  if (l == r)
    return;
  if (x <= mid)
    insert(k << 1, l, mid, x, v);
  else
    insert(k << 1 | 1, mid + 1, r, x, v);
}
void askrank(int k, int l, int r, int x, int y, int val) {
  int mid = (l + r) >> 1;
  if (x <= l && r <= y) {
    ans += sp.rank(k, val);
    return;
  }
  if (x <= mid)
    askrank(k << 1, l, mid, x, y, val);
  if (mid + 1 <= y)
    askrank(k << 1 | 1, mid + 1, r, x, y, val);
}
void change(int k, int l, int r, int pos, int val) {
  int mid = (l + r) >> 1;
  sp.find(k, a[pos]);
  sp.del(k);
  sp.insert(k, val);
  if (l == r)
    return;
  if (pos <= mid)
    change(k << 1, l, mid, pos, val);
  else
    change(k << 1 | 1, mid + 1, r, pos, val);
}
void askpre(int k, int l, int r, int x, int y, int val) {
  int mid = (l + r) >> 1;
  if (x <= l && r <= y) {
    ans = max(ans, sp.find_pre(k, val));
    return;
  }
  if (x <= mid)
    askpre(k << 1, l, mid, x, y, val);
  if (mid + 1 <= y)
    askpre(k << 1 | 1, mid + 1, r, x, y, val);
}
void asksucc(int k, int l, int r, int x, int y, int val) {
  int mid = (l + r) >> 1;
  if (x <= l && r <= y) {
    ans = min(ans, sp.find_succ(k, val));
    return;
  }
  if (x <= mid)
    asksucc(k << 1, l, mid, x, y, val);
  if (mid + 1 <= y)
    asksucc(k << 1 | 1, mid + 1, r, x, y, val);
}
int main() {
#ifdef D
  freopen("input", "r", stdin);
#endif
  n = read(), m = read();
  for (int i = 1; i <= n; i++)
    a[i] = read(), Max = max(Max, a[i]), insert(1, 1, n, i, a[i]);
  for (int i = 1; i <= m; i++) {
    opt = read();
    if (opt == 1) {
      l = read(), r = read(), k = read();
      ans = 0;
      askrank(1, 1, n, l, r, k);
      printf("%d
", ans + 1);
    } else if (opt == 2) {
      l = read(), r = read(), k = read();
      int head = 0, tail = Max + 1;
      while (head != tail) {
        int mid = (head + tail) >> 1;
        ans = 0;
        askrank(1, 1, n, l, r, mid);
        if (ans < k)
          head = mid + 1;
        else
          tail = mid;
      }
      printf("%d
", head - 1);
    } else if (opt == 3) {
      pos = read();
      k = read();
      change(1, 1, n, pos, k);
      a[pos] = k;
      Max = std::max(Max, k);
    } else if (opt == 4) {
      l = read();
      r = read();
      k = read();
      ans = 0;
      askpre(1, 1, n, l, r, k);
      printf("%d
", ans);
    } else if (opt == 5) {
      l = read();
      r = read();
      k = read();
      ans = inf;
      asksucc(1, 1, n, l, r, k);
      printf("%d
", ans);
    }
  }

1.6点分治

void getroot(int x, int fa) {
  size[x] = 1;
  f[x] = 0;
  for (int i = 0; i < G[x].size(); i++) {
    edge &e = G[x][i];
    if (!vis[e.to] && e.to != fa) {
      getroot(e.to, x);
      size[x] += size[e.to];
      f[x] = max(f[x], size[e.to]);
    }
  }
  f[x] = max(f[x], sum - size[x]);
  if (f[x] < f[rt])
    rt = x;
}
void getdeep(int x, int fa) {
  cnt[deep[x]]++;
  for (int i = 0; i < G[x].size(); i++) {
    edge &e = G[x][i];
    if (!vis[e.to] && e.to != fa) {
      deep[e.to] = (deep[x] + e.weigh) % 3;
      getdeep(e.to, x);
    }
  }
}
int cal(int x, int now) {
  cnt[0] = cnt[1] = cnt[2] = 0;
  deep[x] = now;
  getdeep(x, 0);
  return cnt[1] * cnt[2] * 2 + cnt[0] * cnt[0];
}
void work(int x) {
  ans += cal(x, 0); //统计不同子树通过重心的个数
  vis[x] = 1;
#ifndef ONLINE_JUDGE
  printf("In root %d: %d
", rt, ans);
#endif
  for (int i = 0; i < G[x].size(); i++) {
    edge &e = G[x][i];
    if (!vis[e.to]) {
      ans -= cal(e.to, e.weigh); //去除在同一个子树中被重复统计的
      rt = 0;
      sum = size[e.to];
      getroot(e.to, 0);
      work(rt); // Decrease and Conquer
    }
  }
}

1.7树链剖分

void dfs1(int x) {
  vis[x] = size[x] = 1;
  for (int i = 1; i <= 17; i++) {
    if (deep[x] < (1 << i))
      break;
    fa[x][i] = fa[fa[x][i - 1]][i - 1];
  }
  for (int i = head[x]; i; i = e[i].next) {
    if (!vis[e[i].to]) {
      deep[e[i].to] = deep[x] + 1;
      fa[e[i].to][0] = x;
      dfs1(e[i].to);
      size[x] += size[e[i].to];
    }
  }
}
void dfs2(int x, int chain) {
  pl[x] = ++sz;
  que[sz] = x;
  belong[x] = chain;
  int k = 0;
  for (int i = head[x]; i; i = e[i].next)
    if (deep[e[i].to] > deep[x] && size[k] < size[e[i].to])
      k = e[i].to;
  if (!k)
    return;
  dfs2(k, chain);
  for (int i = head[x]; i; i = e[i].next)
    if (e[i].to != k && deep[e[i].to] > deep[x])
      dfs2(e[i].to, e[i].to);
}
void update(int k) {}
void build(int k, int l, int r) {
  t[k].l = l, t[k].r = r, t[k].s = 1, t[k].tag = -1;
  if (l == r) {
    t[k].lc = t[k].rc = value[que[l]];
    return;
  }
  int mid = (l + r) >> 1;
  build(k << 1, l, mid);
  build(k << 1 | 1, mid + 1, r);
  update(k);
}
int lca(int x, int y) {
  if (deep[x] < deep[y])
    std::swap(x, y);
  int t = deep[x] - deep[y];
  for (int i = 0; i <= 17; i++) {
    if (t & (1 << i))
      x = fa[x][i];
  }
  for (int i = 17; i >= 0; i--) {
    if (fa[x][i] != fa[y][i]) {
      x = fa[x][i];
      y = fa[y][i];
    }
  }
  if (x == y)
    return x;
  else
    return fa[x][0];
}
void pushdown(int k) {}
int query(int k, int x, int y) {}//线段树操作
int getcolor(int k, int pos) {}//线段树操作
int solvesum(int x, int f) {
  int sum = 0;
  while (belong[x] != belong[f]) {
    sum += query(1, pl[belong[x]], pl[x]);
    if (getcolor(1, pl[belong[x]]) == getcolor(1, pl[fa[belong[x]][0]]))
      sum--;
    x = fa[belong[x]][0];
  }
  sum += query(1, pl[f], pl[x]);
  return sum;
}
void change(int k, int x, int y, int c) {}//线段树操作
void solvechange(int x, int f, int c) {
  while (belong[x] != belong[f]) {
    change(1, pl[belong[x]], pl[x], c);
    x = fa[belong[x]][0];
  }
  change(1, pl[f], pl[x], c);
}
void solve() {
  dfs1(1);
  dfs2(1, 1);
  build(1, 1, n);
  for (int i = 1; i <= m; i++) {
    char ch[10];
    scanf("%s", ch);
    if (ch[0] == 'Q') {
      int a, b;
      scanf("%d %d", &a, &b);
      int t = lca(a, b);
      printf("%d
", solvesum(a, t) + solvesum(b, t) - 1);
    } else {
      int a, b, c;
      scanf("%d %d %d", &a, &b, &c);
      int t = lca(a, b);
      solvechange(a, t, c);
      solvechange(b, t, c);
    }
  }
}

1.8 Link-Cut Tree

对于树上的操作，我们现在已经有了树链剖分可以处理这些问题。然而树链剖分不支持动态维护树上的拓扑结构。所以我们需要Link-Cut Tree(lct)来解决这种动态树问题。顺带一提的是，动态树也是Tarjan发明的。

首先我们介绍一个概念：Preferred path（实边），其他的边都是虚边。我们使用splay来实时地维护这条路径。

lct的核心操作是access。access操作可以把虚边变为实边，通过改变splay的拓扑结构来维护实边。

有了这个数据结构，我们依次来考虑两个操作。

对于链接两个节点，我们需要首先把x节点变为他所在树的根节点，然后直接令fa[x] = y即可。

怎样换根呢？稍微思考一下可以发现，我们直接把从根到他的路径反转即可。

对于第二种操作，我们直接断开拓扑关系即可。

另外实现的时候要注意，splay的根节点的父亲是他的上一个节点。所以zig和splay的写法应该格外注意。

inline bool isroot(int x) { return ch[fa[x]][0] != x && ch[fa[x]][1] != x; }
void pushdown(int k) {
  if (rev[k]) {
    rev[k] = 0;
    rev[ch[k][0]] ^= 1;
    rev[ch[k][1]] ^= 1;
    std::swap(ch[k][0], ch[k][1]);
  }
}
void zig(int x) {
  int y = fa[x], z = fa[y], l = (ch[y][1] == x), r = l ^ 1;
  if (!isroot(y))
    ch[z][ch[z][1] == y] = x;
  fa[ch[y][l] = ch[x][r]] = y;
  fa[ch[x][r] = y] = x;
  fa[x] = z;
}
void splay(int x) {
  stack<int> st;
  st.push(x);
  for (int i = x; !isroot(i); i = fa[i])
    st.push(fa[i]);
  while (!st.empty()) {
    pushdown(st.top());
    st.pop();
  }
  for (int y = fa[x]; !isroot(x); zig(x), y = fa[x])
    if (!isroot(y))
      zig((ch[fa[y]][0] == y) == (ch[y][0] == x) ? y : x);
}
void access(int x) {
  int t = 0;
  while (x) {
    splay(x);
    ch[x][1] = t;
    t = x;
    x = fa[x];
  }
}
void rever(int x) {
  access(x);
  splay(x);
  rev[x] ^= 1;
}
void link(int x, int y) {
  rever(x);
  fa[x] = y;
  splay(x);
}
void cut(int x, int y) {
  rever(x);
  access(y);
  splay(y);
  ch[y][0] = fa[x] = 0;
}
int find(int x) {
  access(x);
  splay(x);
  int y = x;
  while (ch[y][0])
    y = ch[y][0];
  return y;
}

1.9 KMP

对于字符串S的前i个字符构成的子串，既是它的后缀又是它的前缀的字符串中（它本身除外），最长的长度记作next[i]

多用于DP

for (int i = 2; i <= m; i++) {
    while (j > 0 && ch[j + 1] != ch[i])
      j = p[j];
    if (ch[j + 1] == ch[i])
      j++;
    p[i] = j;
  }

1.10 AC自动机

KMP在Trie上的扩展.

void insert(char s[101]) {
  int now = 1, c;
  for (int i = 0; i < strlen(s); i++) {
    c = s[i] - 'A' + 1;
    if (a[now][c])
      now = a[now][c];
    else
      now = a[now][c] = ++sz;
  }
  leaf[now] = 1;
}
void ac() {
  std::queue<int> q;
  q.push(1);
  point[1] = 0;
  while (!q.empty()) {
    int u = q.front();
    q.pop();
    for (int i = 1; i <= 26; i++) {
      if (!a[u][i])
        continue;
      int k = point[u];
      while (!a[k][i])
        k = point[k];
      point[a[u][i]] = a[k][i];
      if (leaf[a[k][i]])
        leaf[a[u][i]] = 1;
      q.push(a[u][i]);
    }
  }
}

1.11 后缀数组

void getsa(int sa[maxn], int rank[maxn], int Sa[maxn], int Rank[maxn]) {
  for (int i = 1; i <= n; i++)
    v[rank[sa[i]]] = i;
  for (int i = n; i >= 1; i--)
    if (sa[i] > k)
      Sa[v[rank[sa[i] - k]]--] = sa[i] - k;
  for (int i = n - k + 1; i <= n; i++)
    Sa[v[rank[i]]--] = i;
  for (int i = 1; i <= n; i++)
    Rank[Sa[i]] = Rank[Sa[i - 1]] + (rank[Sa[i - 1]] != rank[Sa[i]] ||
                                     rank[Sa[i - 1] + k] != rank[Sa[i] + k]);
}
void getheight(int sa[maxn], int rank[maxn]) {
  int i, k = 0;
  for (i = 1; i <= n; height[rank[i++]] = k) {
    if (k)
      k--;
    int j = sa[rank[i] - 1];
    while (a[i + k] == a[j + k])
      k++;
  }
}
void da() {
  p = 0, q = 1, k = 1;
  for (int i = 1; i <= n; i++)
    v[a[i]]++;
  for (int i = 1; i <= 2; i++)
    v[i] += v[i - 1];
  for (int i = 1; i <= n; i++)
    sa[p][v[a[i]]--] = i;
  for (int i = 1; i <= n; i++)
    rank[p][sa[p][i]] =
        rank[p][sa[p][i - 1]] + (a[sa[p][i - 1]] != a[sa[p][i]]);
  while (k < n) {
    getsa(sa[p], rank[p], sa[q], rank[q]);
    p ^= 1;
    q ^= 1;
    k <<= 1;
  }
  getheight(sa[p], rank[p]);
}

1.12 后缀自动机

struct Suffix_Automaton {
  ll fa[maxn], trans[maxn][26], len[maxn], right[maxn];
  ll last, root, sz;
  bool flag[maxn];
  void init() {
    memset(flag, 0, sizeof(flag));
    sz = 0;
    last = root = ++sz;
  }
  void insert(ll x) {
    ll p = last, np = last = ++sz;
    len[np] = len[p] + 1;
    flag[np] = 1;
    right[np] = right[p] + 1;
    for (; !trans[p][x]; p = fa[p])
      trans[p][x] = np;
    if (p == 0)
      fa[np] = root;
    else {
      ll q = trans[p][x];
      if (len[q] == len[p] + 1) {
        fa[np] = q;
      } else {
        ll nq = ++sz;
        fa[nq] = fa[q];
        memcpy(trans[nq], trans[q], sizeof(trans[q]));
        len[nq] = len[p] + 1;
        fa[q] = fa[np] = nq;
        for (; trans[p][x] == q; p = fa[p])
          trans[p][x] = nq;
      }
    }
  }
} sam;

1.13 Manacher

void manacher() {
  int mx = 1, id = 1;
  for (int i = n; i; i--)
    str[i * 2] = '#', str[i * 2 - 1] = str[i];
  n <<= 1;
  for (int i = 1; i <= n; i++) {
    p[i] = std::min(p[id * 2 - i], mx - i);
    while (i - p[i] > 0 && str[i - p[i]] == str[i + p[i]]) {
      int al = (i - p[i]) / 2 + 1;
      int ar = (i + p[i] + 1) / 2;
      // printf("%d %d
", al, ar);
      sam.query(al, ar);
      p[i]++;
    }
    if (i + p[i] > mx)
      mx = i + p[i], id = i;
  }
}

1.14 分块

随便给一个例题吧.

给定一个数列，您需要支持一下两种操作：1.给[l,r]同加一个数. 2.询问[l,r]中有多少数字大于或等于v.

把数据分为(sqrt n)一份，那么对于每一个查询，我们都可以把这个查询分为(sqrt n)个区间，修改的时候也是(O(sqrt n))的级别，所以总的复杂度就是(O(sqrt n log sqrt n))

具体地，对于每一块，我们都存储排序前和排序后的序列，这样我们就解决了这个题。

#include <algorithm>
#include <cctype>
#include <cmath>
#include <cstdio>
int n, q, m, block;
const int maxn = 1000001;
int a[maxn], b[maxn], pos[maxn], add[maxn];
using std::sort;
using std::min;
inline int read() {}
inline void reset(int x) {
  int l = (x - 1) * block + 1, r = min(x * block, n);
  for (int i = l; i <= r; i++)
    b[i] = a[i];
  sort(b + l, b + r + 1);
}
inline int find(int x, int v) {
  int l = (x - 1) * block + 1, r = min(x * block, n);
  int last = r;
  while (l <= r) {
    int mid = (l + r) >> 1;
    if (b[mid] < v)
      l = mid + 1;
    else
      r = mid - 1;
  }
  return last - l + 1;
}
inline void update(int x, int y, int v) {
  if (pos[x] == pos[y]) {
    for (int i = x; i <= y; i++)
      a[i] = a[i] + v;
  } else {
    for (int i = x; i <= pos[x] * block; i++)
      a[i] = a[i] + v;
    for (int i = (pos[y] - 1) * block + 1; i <= y; i++)
      a[i] = a[i] + v;
  }
  reset(pos[x]);
  reset(pos[y]);
  for (int i = pos[x] + 1; i < pos[y]; i++)
    add[i] += v;
}
inline int query(int x, int y, int v) {
  int sum = 0;
  if (pos[x] == pos[y]) {
    for (int i = x; i <= y; i++)
      if (a[i] + add[pos[i]] >= v)
        sum++;
  } else {
    for (int i = x; i <= pos[x] * block; i++)
      if (a[i] + add[pos[i]] >= v)
        sum++;
    for (int i = (pos[y] - 1) * block + 1; i <= y; i++)
      if (a[i] + add[pos[i]] >= v)
        sum++;
    for (int i = pos[x] + 1; i < pos[y]; i++)
      sum += find(i, v - add[i]);
  }
  return sum;
}
int main() {
#ifndef ONLINE_JUDGE
  freopen("input", "r", stdin);
#endif
  n = read(), q = read();
  if (n >= 500000)
    block = 3676;
  else if (n >= 5000) {
    block = 209;
  } else
    block = int(sqrt(n));
  for (int i = 1; i <= n; i++) {
    a[i] = read();
    pos[i] = (i - 1) / block + 1;
    b[i] = a[i];
  }
  if (n % block)
    m = n / block + 1;
  else
    m = n / block;
  for (int i = 1; i <= m; i++)
    reset(i);
  for (int i = 1; i <= q; i++) {
    char ch[5];
    int x, y, v;
    scanf("%s", ch);
    x = read(), y = read(), v = read();
    if (ch[0] == 'M')
      update(x, y, v);
    else
      printf("%d
", query(x, y, v));
  }
}

1.15 莫队算法

如果你知道了[L,R]的答案。你可以在O(1)的时间下得到[L,R-1]和[L,R+1]和[L-1,R]和[L+1,R]的答案的话。就可以使用莫队算法。
对于莫队算法我感觉就是暴力。只是预先知道了所有的询问。可以合理的组织计算每个询问的顺序以此来降低复杂度。要知道我们算完[L,R]的答案后现在要算[L',R']的答案。由于可以在O(1)的时间下得到[L,R-1]和[L,R+1]和[L-1,R]和[L+1,R]的答案.所以计算[L',R']的答案花的时间为|L-L'|+|R-R'|。如果把询问[L,R]看做平面上的点a(L,R).询问[L',R']看做点b(L',R')的话。那么时间开销就为两点的曼哈顿距离。所以对于每个询问看做一个点。我们要按一定顺序计算每个值。那开销就为曼哈顿距离的和。要计算到每个点。那么路径至少是一棵树。所以问题就变成了求二维平面的最小曼哈顿距离生成树。
关于二维平面最小曼哈顿距离生成树。感兴趣的可以参考胡泽聪大佬的这篇文章

这样只要顺着树边计算一次就ok了。可以证明时间复杂度为(O(n∗sqrt n)).

但是这种方法编程复杂度稍微高了一点。所以有一个比较优雅的替代品。那就是先对序列分块。然后对于所有询问按照L所在块的大小排序。如果一样再按照R排序。然后按照排序后的顺序计算。为什么这样计算就可以降低复杂度呢。

一、i与i+1在同一块内，r单调递增，所以r是O(n)的。由于有n^0.5块,所以这一部分时间复杂度是n^1.5。
二、i与i+1跨越一块，r最多变化n，由于有n^0.5块，所以这一部分时间复杂度是n^1.5
三、i与i+1在同一块内时变化不超过n^0.5，跨越一块也不会超过2*n^0.5，不妨看作是n^0.5。由于有n个数，所以时间复杂度是n^1.5
于是就变成了Θ(n1.5)

#include <algorithm>
#include <cmath>
#include <cstdio>
#include <cstring>
#include <iostream>
const int maxn = 50010;
#define ll long long
ll num[maxn], up[maxn], dw[maxn], ans, aa, bb, cc;
int col[maxn], pos[maxn];
struct qnode {
  int l, r, id;
} qu[maxn];
bool cmp(qnode a, qnode b) {
  if (pos[a.l] == pos[b.l])
    return a.r < b.r;
  else
    return pos[a.l] < pos[b.l];
}
ll gcd(ll x, ll y) {
  ll tp;
  while ((tp = x % y)) {
    x = y;
    y = tp;
  }
  return y;
}
void update(int x, int d) {
  ans -= num[col[x]] * num[col[x]];
  num[col[x]] += d;
  ans += num[col[x]] * num[col[x]];
}
int main() {
  int n, m, bk, pl, pr, id;
#ifndef ONLINE_JUDGE
  freopen("input", "r", stdin);
#endif
  scanf("%d %d", &n, &m);
  memset(num, 0, sizeof(num));
  bk = ceil(sqrt(1.0 * n));
  for (int i = 1; i <= n; i++) {
    scanf("%d", &col[i]);
    pos[i] = (i - 1) / bk;
  }
  for (int i = 0; i < m; i++) {
    scanf("%d %d", &qu[i].l, &qu[i].r);
    qu[i].id = i;
  }
  std::sort(qu, qu + m, cmp);
  pl = 1, pr = 0;
  ans = 0;
  for (int i = 0; i < m; i++) {
    id = qu[i].id;
    if (qu[i].l == qu[i].r) {
      up[id] = 0, dw[id] = 1;
      continue;
    }
    if (pr < qu[i].r) {
      for (int j = pr + 1; j <= qu[i].r; j++)
        update(j, 1);
    } else {
      for (int j = pr; j > qu[i].r; j--)
        update(j, -1);
    }
    pr = qu[i].r;
    if (pl < qu[i].l) {
      for (int j = pl; j < qu[i].l; j++)
        update(j, -1);
    } else {
      for (int j = pl - 1; j >= qu[i].l; j--)
        update(j, 1);
    }
    pl = qu[i].l;
    aa = ans - qu[i].r + qu[i].l - 1;
    bb = (ll)(qu[i].r - qu[i].l + 1) * (qu[i].r - qu[i].l);
    cc = gcd(aa, bb);
    aa /= cc, bb /= cc;
    up[id] = aa, dw[id] = bb;
  }
  for (int i = 0; i < m; i++)
    printf("%lld/%lld
", up[i], dw[i]);
}

1.16 整体二分&CDQ分治

GRAPHIC

2.图论

2.1图的连通性

2.1.1 双连通分量

• 定理: 在无向连通图G的DFS树中, 非根节点u是G的割顶当且仅当u存在一個子节点v, 使得v及其后代都没有反向边连回u的祖先.
• 设low(u)为u及其后代所能连回的最早的祖先的pre值, 则定理中的条件就是:
• 节点u存在一个子节点v, 使得low(v) >= pre(u).
• 对于一个连通图, 如果任意两点存在至少两条"点不重复"的路径, 就说这个图是点-双连通的, 这个要求等价于任意两条边都在同一个简单环中, 即内部无割顶. 类似的定义边-双连通. 对于一张无向图, 点-双连通的极大子图称为双连通分量.
• 不同双连通分量最多只有一个公共点, 且它一定是割顶. 任意割顶都是两个不同双连通分量的公共点.

stack<Edge> S;
int dfs(int u, int fa) {
  int lowu = pre[u] = ++dfs_clock;
  int child = 0;
  for(int i = 0; i < G[u].size(); i++) {
    int v = G[u][i];
    Edge e = (Edge){u, v};
    if(!pre[v]) {
      S.push(e);
      child++;
      int lowv = dfs(v, u);
      lowu = min(lowu, lowv);
      if(lowv >= pre[u]) {
        iscut[u] = true;
        bcc_cnt++;
        bcc[bcc_cnt].clear();
        for(;;) {
          Edge x = S.top(); S.pop();
          if(bccno[x.u] != bcc_cnt) {bcc[bcc_cnt].push_back(x.u); bccno[x.u] = bcc_cnt;}
          if(bccno[x.v] != bcc_cnt) {bcc[bcc_cnt].push_back(x.v); bccno[x.v] = bcc_cnt;}
          if(x.u == u && x.v == v) break;
        }
      }
    }
    else if(pre[v] < pre[u] && v != fa) {
      S.push(e);
      lowu = min(lowu, pre[v]);
    }
  }
  if(fa < 0 && child == 1) iscut[u] = 0;
  return lowu;
}

• 边-双连通分量可以使用更简单的方法求出, 分两个步骤, 先做一次dfs标记出所有的桥, 然后再做一次dfs找出边-双连通分量. 因为边-双连通分量是没有公共节点的, 所以只要在第二次dfs的时候保证不经过桥即可.

2.1.2 强连通分量

kosaraju算法.

void dfs(int v) {
  vis[v] = true;
  for (int i = 0; i < G[v].size(); i++) {
    if (!vis[G[v][i]])
      dfs(G[v][i]);
  }
  vs.push_back(v);
}
void rdfs(int v, int k) {
  vis[v] = true;
  cnt[v] = k;
  for (int i = 0; i < rG[v].size(); i++) {
    if (!vis[rG[v][i]])
      rdfs(rG[v][i], k);
  }
  vs.push_back(v);
  sc[k].push_back(v);
}
int scc() {
  memset(vis, 0, sizeof(vis));
  vs.clear();
  for (int v = 1; v <= n; v++) {
    if (!vis[v])
      dfs(v);
  }
  memset(vis, 0, sizeof(vis));
  int k = 0;
  for (int i = vs.size() - 1; i >= 0; i--) {
    if (!vis[vs[i]]) {
      rdfs(vs[i], k++);
    }
  }
  return k;
}

2.2 最短路与最小生成树

2.2.1 SPFA

虽然是NOIp(professional)知识, 但是由于在省选中非常常用, 还是写一下.

最短路算法也会在分层图中考察.

spfa也可以运用在DP中的转移.

void spfa() {
  memset(dist, 0x3f, sizeof(dist));
  dist[s][0] = 0;
  queue<state> q;
  q.push((state){s, 0});
  memset(inq, 0, sizeof(inq));
  inq[s][0] = 1;
  while (!q.empty()) {
    state u = q.front();
    q.pop();
    inq[u.pos][u.k] = 0;
    for (int i = 0; i < G[u.pos].size(); i++) {
      edge &e = G[u.pos][i];
      if (dist[e.to][u.k] > dist[u.pos][u.k] + e.value) {
        dist[e.to][u.k] = dist[u.pos][u.k] + e.value;
        if (!inq[e.to][u.k]) {
          q.push((state){e.to, u.k});
          inq[e.to][u.k] = 1;
        }
      }
      if (u.k < k && dist[e.to][u.k + 1] > dist[u.pos][u.k]) {
        dist[e.to][u.k + 1] = dist[u.pos][u.k];
        if (!inq[e.to][u.k + 1]) {
          q.push((state){e.to, u.k + 1});
          inq[e.to][u.k + 1] = 1;
        }
      }
    }
  }
}

spfa可以用来判负环. 所谓负环就是环上边权和为负的环. 一般使用dfs版本spfa判负环.

double dist[maxn];
inline void spfa(int x) {
  int i;
  vis[x] = false;
  for (i = 0; i < rg[x].size(); i++) {
    edge &e = rg[x][i];
    if (dist[e.to] > dist[x] + e.value)
      if (!vis[e.to]) {
        flag = true;
        break;
      } else {
        dist[e.to] = dist[x] + e.value;
        spfa(e.to);
      }
  }
  vis[x] = true;
}
bool check(double lambda) {
  for (int i = 1; i <= n; i++) {
    rg[i].clear();
    for (int j = 0; j < G[i].size(); j++) {
      rg[i].push_back((edge){G[i][j].to, (double)G[i][j].value - lambda});
    }
  }
  memset(vis, 1, sizeof(vis));
  memset(dist, 0, sizeof(dist));
  flag = false;
  for (int i = 1; i <= n; i++) {
    spfa(i);
    if (flag)
      return true;
  }
  return false;
}

2.2.2 动态最小生成树

最小生成树算是很常见的考点.

关于最小生成树, 我们有以下结论:

• 对于连通图中的任意一个环 C ：如果C中有边e的权值大于该环中任意一个其它的边的权值，那么这个边不会是最小生成树中的边.

• 在一幅连通加权无向图中，给定任意的切分，它的横切边中权值最小的边必然属于图的最小生成树。

• 如果图的具有最小权值的边只有一条，那么这条边包含在任意一个最小生成树中。

• 次小生成树: 树上倍增+lca

• 两个点之间的最大权最小路径一定在最小生成森林上(水管局长)

• 欧几里德最小生成树
  动态最小生成树: 使用Link-Cut Tree维护.

• 矩阵树定理(Matrix-Tree)

下面我们介绍一种新的方法——Matrix-Tree定理(Kirchhoff矩阵-树定理)。Matrix-Tree定理是解决生成树计数问题最有力的武器之一。它首先于1847年被Kirchhoff证明。在介绍定理之前，我们首先明确几个概念：
1、G的度数矩阵(D[G])是一个(n imes n)的矩阵，并且满足：当(i ot = j)时,(d_{ij}=0)；当(i=j)时，(d_{ij})等于(v_i)的度数。
2、G的邻接矩阵(A[G])也是一个(n imes n)的矩阵， 并且满足：如果(v_i)、(v_j)之间有边直接相连，则(a_{ij})=1，否则为0。
我们定义(G)的Kirchhoff矩阵(也称为拉普拉斯算子)C[G]为C[G]=D[G]-A[G]，则Matrix-Tree定理可以描述为：G的所有不同的生成树的个数等于其Kirchhoff矩阵C[G]任何一个n-1阶主子式的行列式的绝对值。所谓n-1阶主子式，就是对于r(1≤r≤n)，将C[G]的第r行、第r列同时去掉后得到的新矩阵，用Cr[G]表示。

• kruskal 算法: 贪心地选取每一条边

2.3网络流

2.3.1 预备知识

• 流网络(G=(V,E))是一个有向图, 其中每条边(<u, v> in E)均为有一非负容量(c(u, v) geqslant 0), 规定: 若(<u,v> ot in E), 则(c(u,v)=0). 网络中有两个特殊点(s)和(t).
• 网络的流是一个实值函数(f):(V imes V ightarrow R), 且满足三个性质: 容量限制, 反对称性, 流守恒性.
• 最大的流是指该网络中流值最大的流.
• 残留网络由可以容纳更多流的边构成.
• 增广路径(p)为残留网络上(s)到(t)的一条简单路径.
• 流网络(G=(V, E))的割([S, T])将点集划分为(S)和(T)两部分, 使得(s in S and t in T). 符号([S, T]={<u,v>|<u,v> in E, u in S, v in T}), 通过割的净流为(f(S,T)), 容量定义为(c(S,T)).
• 一个网络的最小割就是网络中容量最小的割.

2.3.2 最大流最小割定理与线性规划

首先我们假设读者已经有了线性规划的基本知识.

最大流问题的线性规划描述:

[egin{alignat}{2} maxquad &f_{ts} &{}& ag{LP1} label{eqn - lp}\ mbox{s.t.}quad &f_{u,v}leqslant c_{u,v}, &quad& (u,v)in E\ &sum_{v} f_{uv} = sum_v f_{vu}, &{}& u in V\ & f_{uv} geqslant 0, &{}& (u,v) in E cup{(t,s)} end{alignat} ]

最小割问题的线性规划描述:

[egin{alignat}{2} minquad &sum_{(u,v) in E}c_{uv}d_{uv} &{}& ag{LP2} \ mbox{s.t.}quad &d_{u,v}-p_u+p_v &geqslant 0, &quad& (u,v)in E\ &p_s-p_t &geqslant 1\ &p_u, d_{uv} in {0, 1} end{alignat} ]

令(p_u=[u in S]), (d_{uv}=max{p_u-p_v, 0}).

考虑最大流的对偶: 记由容量限制产生的变量为(d_{uv}), 由点(u)的流量守恒产生的变量为(p_u), 那么对偶问题就是:

[egin{alignat}{2} minquad &sum_{(u,v) in E}c_{uv}d_{uv} &{}& ag{LP3} \ mbox{s.t.}quad &d_{u,v}-p_u+p_v &geqslant 0, &quad& (u,v)in E\ &p_s-p_t &geqslant 1\ &d_{uv} &geqslant 0, &{}&(u,v)in E end{alignat} ]

我们得出结论: (最大流最小割定理)给定一个源为(s), 汇为(t)的网络, 则(s,t)的最大流等于(s,t)的最小割.

2.3.3 最大流算法

2.3.3.1 Dinic算法

int dist[maxn], iter[maxn];
inline void bfs(int s) {
  memset(dist, -1, sizeof(dist));
  dist[s] = 0;
  queue<int> q;
  q.push(s);
  while (!q.empty()) {
    int u = q.front();
    q.pop();
    for (int i = 0; i < G[u].size(); i++) {
      edge &e = edges[G[u][i]];
      if (e.cap > 0 && dist[e.to] == -1) {
        dist[e.to] = dist[u] + 1;
        q.push(e.to);
      }
    }
  }
}
inline int dfs(int s, int t, int flow) {
  if (s == t)
    return flow;
  for (int &i = iter[s]; i < G[s].size(); i++) {
    edge &e = edges[G[s][i]];
    if (e.cap > 0 && dist[e.to] > dist[s]) {
      int d = dfs(e.to, t, min(e.cap, flow));
      if (d > 0) {
        e.cap -= d;
        edges[G[s][i] ^ 1].cap += d;
        return d;
      }
    }
  }
  return 0;
}
inline int dinic(int s, int t) {
  int flow = 0;
  while (1) {
    bfs(s);
    if (dist[t] == -1)
      return flow;
    memset(iter, 0, sizeof(iter));
    int d;
    while (d = dfs(s, t, inf))
      flow += d;
  }
  return flow;
}

2.3.3.2 费用流

泛指一种与费用相关的流算法.EK算法比较常用

bool spfa(ll &flow, ll &cost) {
  for (int i = 0; i <= n + 1; i++) {
    dist[i] = -inf;
  }
  memset(inq, 0, sizeof(inq));
  dist[s] = 0, inq[s] = 1, pre[s] = 0, fi[s] = inf;
  queue<int> q;
  q.push(s);
  while (!q.empty()) {
    int u = q.front();
    q.pop();
    inq[u] = 0;
    for (int i = 0; i < G[u].size(); i++) {
      edge &e = E[G[u][i]];
      if (e.cap > e.flow && dist[e.to] < dist[u] + e.cost) {
        dist[e.to] = dist[u] + e.cost;
        pre[e.to] = G[u][i];
        fi[e.to] = min(fi[u], e.cap - e.flow);
        if (!inq[e.to]) {
          q.push(e.to);
          inq[e.to] = 1;
        }
      }
    }
  }
  if (dist[t] <= -inf)
    return false;
  if (cost + dist[t] * fi[t] < 0) { 
    ll temp = cost / (-dist[t]); //temp:还能够增加的流
    flow += temp;
    return false;
  }
  flow += fi[t];
  cost += dist[t] * fi[t];
  int u = t;
  while (u != s) {
    E[pre[u]].flow += fi[t];
    E[pre[u] ^ 1].flow -= fi[t];
    u = E[pre[u]].from;
  }
  return true;
}
ll mcmf(int s, int t) {
  ll flow = 0;
  ll cost = 0;
  while (spfa(flow, cost))
    ;
  return flow;
}

2.3.4 建模方法

2.3.4.1 基本建模

• 多个源点和汇点(超级源点, 超级汇点)
• 无向图: 拆成两条边
• 顶点容量限制: 拆点
• 不相交的两条路径: 拆点
• 上下界网络流:
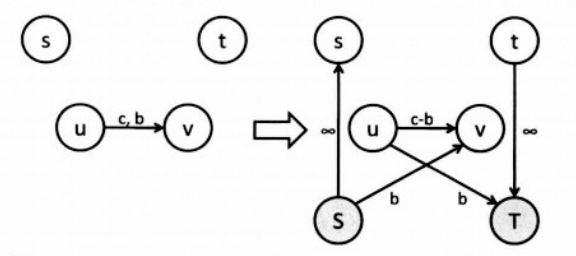
• 上下界费用流:
• 图部分发生变化: 重复利用之前的结果

1. 容量增加, 直接跑最大流
2. 容量减少, 如果(f(e) leq c(e)-1), 那么不用动, 否则退流

for (int i = 1; i <= n; i++) {
      int now = cc[i].id;
      int u = now, v = now + n;
      bfs(u);
      if (dist[v] != -1)
        continue;
      rec[tot++] = now;
      dinic(t, v);
      dinic(u, s);
      edges[(now - 1) * 2].cap = edges[(now - 1) * 2 + 1].cap = 0;
}

• 容量为负数: 适当变形
• 费用为负数的情况:

1. 消负圈
2. 通过适当的变形. 比如说, 如果每次增广所用的边数都是相同的(记做m), 那么把所有边的费用都加上常数(k), 然后从最短路减去(mk)就得到了原图最短路的长度
3. 

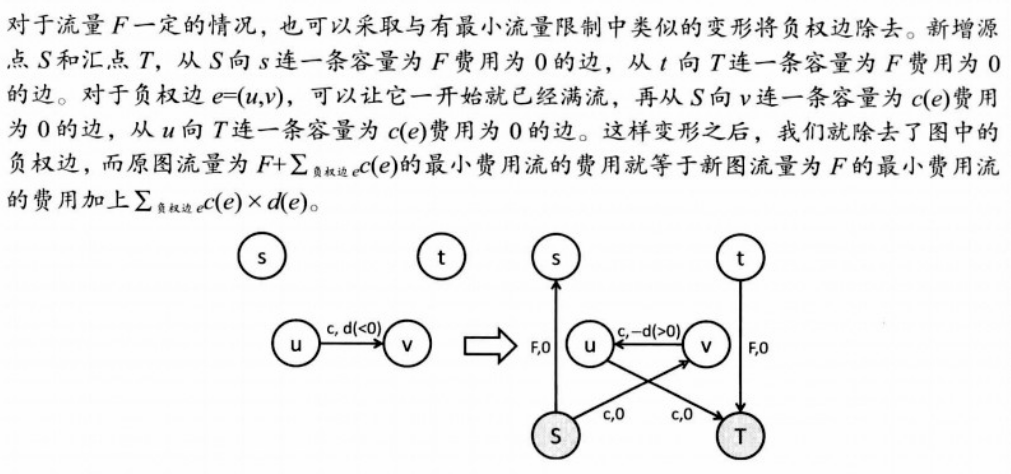
2.3.4.2 最大流建模

• 与棋盘有关的题目可以考虑最大流

2.3.4.3 最小割建模

• 用容量为(infty)的边表示冲突
• 从两点关系的角度进行最小割建模

2.3.4.4 费用流建模

2.3.4.5 流量平衡思想

2.4二分图

• 二分图, 指顶点可以分为两个不相交的几个(U)和(V)((U and V)皆为独立集), 使得在同一个集内的顶点不相邻的图.
• 无向图G为二分图(Leftrightarrow)G至少有两个顶点, 且所有回路的长度均为偶数(Leftrightarrow)没有奇圈
• 最大边独立集的基数等于最大独立集的基数
• 最大独立集的基数和最大匹配基数之和, 等于顶点数目.
• 对于连通的二分图: 最小顶点覆盖集的基数等于最大匹配的基数
• Hall定理是一个用于判定二分图是否具有最大匹配的定理。
  首先对于二分图G=(X∪Y,E)，点集被分为了XX和YY两部分。
  是否具有最大匹配，首先一个最基本的条件就是|X|=|Y||X|=|Y|。
  Hall定理则在此基础上给出了一个更强的条件。
  首先对于一个点集T⊆X，定义Γ(T)Γ(T)如下：
  Γ(T)={v∣u→v∈E,u∈T,v∈Y}
  Γ(T)={v∣u→v∈E,u∈T,v∈Y}
  即表示TT中所有点能够直接到达的YY中的点的集合。
  
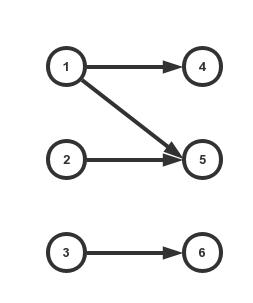
  上图中，Γ({1,3})={4,5,6}Γ({1,3})={4,5,6}。
  那么Hall条件则用于判断一个二分图是否存在最大匹配。Hall条件如下：
  对于任意的点集T⊆X，均存在：
  |T|≤|Γ(T)|
  |T|≤|Γ(T)|
  那么此二分图必定存在最大匹配。

2.5 其他常用结论

• 对于不存在孤立点的图，|最大匹配|+|最小边覆盖| = |V|

• 最大独立集合 + 最小顶点覆盖 = V

• 对于二分图：|最大匹配| = |最小顶点覆盖|

• 平面圖的頂點個數、邊數和面的個數之間有一個以歐拉命名的公式：

  其中，V是頂點的数目，E是邊的數目，F是面的數目，C是组成圖形的連通部分的數目。當圖是單連通圖的時候，公式簡化為：

• 任何一个平面图的对偶图仍然是平面图

MATHEMATICS

3.数学知识

3.1数论

3.1.1扩展欧几里德算法

首先我们有欧几里德算法：

[gcd(a, b) = gcd(a mod b, b) ]

扩展欧几里德算法解决了这样的问题：

[ax + by = gcd(a,b) ]

我们先考察一种特殊的情况：

当(b=0)时，我们直接可以有解：

[egin{eqnarray} left{ egin{array}{lll} x = 1 \ y = 0 end{array} ight. end{eqnarray} ]

一般地，我们令(c = a mod b)，递归地解下面的方程：

[bx^{'}+cy^{'}=gcd(b,c) ]

根据欧几里德算法，有

[bx^{'}+cy^{'}=gcd(a,b) ]

根据(mod)的定义我们可以有

[c = a - blfloorfrac{a}{b} floor ]

带入原式

[bx^{'}+(a - blfloorfrac{a}{b} floor)y^{'}=gcd(a,b) ]

为了体现与(a,b)的关系

[ay^{'}+b(x^{'}-lfloorfrac{a}{b} floor y^{'})=gcd(a,b) ]

所以这样就完成了回溯。

这个算法的思想体现在了下面的程序里。

void gcd(int a, int b, int &d, int &x, int &y) {
  if(!b) {d = a; x = 1; y = 0; }
  else { gcd(b, a%b, d, y, x); y -= x * (a/b); }
}

3.1.2线性筛与积性函数

3.1.2.1线性筛素数

首先给出线性筛素数的程序。

void get_su(int n) {
  tot = 0;
  for(int i = 2; i <= n; i++) {
    if(!check[i]) prime[tot++] = i;
    for(int j = 0; j < tot; j++) {
      if(i * prime[j] > n) break;
      check[i * prime[j]] = true;
      if(i % prime[j] == 0) break;
    }
  }
}

可以证明的是，每个合数都仅仅会被他的最小质因数筛去，这段代码的时间复杂度是(Theta (n))的，也就是所谓线性筛。

证明：设合数(n)最小的质因数为(p)，它的另一个大于(p)的质因数为(p^{'})，另(n = pm=p^{'}m^{'})。 观察上面的程序片段，可以发现(j)循环到质因数(p)时合数n第一次被标记（若循环到(p)之前已经跳出循环，说明(n)有更小的质因数），若也被(p^{'})标记，则是在这之前（因为(m^{'}<m)），考虑(i)循环到(m^{'})，注意到(n=pm=p^{'}m^{'})且(p,p^{'})为不同的质数，因此(p|m^{'})，所以当j循环到质数p后结束，不会循环到(p^{'})，这就说明(n)不会被(p^{'})筛去。

3.1.2.2积性函数

• 考虑一个定义域为(mathbb{N}^{+})的函数(f)（数论函数），对于任意两个互质的正整数(a,b)，均满足

[f(ab) = f(a)f(b)$$，则函数*f*被称为积性函数。 * 如果对于任意两个正整数$a,b$，都有$f(ab)=f(a)f(b)$，那么就被称作完全积性函数。 容易看出，对于任意积性函数，$f(1)=1$。 * 考虑一个大于1的正整数$N$，设$N = prod p_{i}^{a_i}$，那么 $$f(N)=f(prod p_i^{a_i})=prod f(p_i^{a_i})$$，如果$f$还满足完全积性，那么 $$f(N)=prod f(p_i)^{a_i}]

• 如果(f)是一个任意的函数，它使得和式(g(m) = sum_{d|m}f(d))为积性函数，那么(f)也一定是积性函数。
• 积性函数的Dirichlet前缀和也是积性函数。这个定理是上面定理的反命题。
• 两个积性函数的Dirichlet卷积也是积性函数。

3.1.2.3欧拉函数(varphi)

• (varphi(n))表示(1..n)中与(n)互质的整数个数。
• 我们有欧拉定理：

[n^{varphi(m)}equiv 1 pmod m nperp m ]

可以使用这个定理计算逆元。

• 如果(m)是一个素数幂，则容易计算(varphi(m))，因为有$n perp p^{k} Leftrightarrow p mid n $ 。在({0,1,...,p^k-1})中的(p)的倍数是({0, p, 2p, ..., p^k-p})，从而有(p^{k-1})个，剩下的计入(varphi(p^k))

[varphi(p^k) = p^k-p^{k-1}=(p-1)p^{k-1} ]

• 由上面的推导我们不难得出欧拉函数一般的表示：

[varphi(m) = prod_{p|m}(p^{m_p}-p^{m_p-1}) = m prod_{p|m}(1-frac{1}{p})=prod(p-1)p^{m_p-1} ]

• 运用Mobius反演，不难得出(sum_{d|n}varphi(d) = n)。
• 当(n>1)时，(1..n)中与(n)互质的整数和为(frac{nvarphi(n)}{2})
• 降幂大法$$A^B mod C=A^{B mod varphi(C)+varphi(C)} mod C$$

3.1.2.4线性筛法求解积性函数

• 积性函数的关键是如何求(f(p^k))。

• 观察线性筛法中的步骤，筛掉n的同时还得到了他的最小的质因数(p)，我们希望能够知道(p)在(n)中的次数，这样就能够利用(f(n)=f(p^k)f(frac{n}{p^k}))求出(f(n))。

• 令(n=pm)，由于(p)是(n)的最小质因数，若(p^2|n)，则(p|m)，并且(p)也是(m)的最小质因数。这样在筛法的同时，记录每个合数最小质因数的次数，就能算出新筛去合数最小质因数的次数。

• 但是这样还不够，我们还要能够快速求解(f(p^k))，这时一般就要结合(f)函数的性质来考虑。

• 例如欧拉函数(varphi)，(varphi(p^k)=(p-1)p^{k-1})，因此进行筛法求(varphi(p*m))时，如果(p|m)，那么(p*m)中(p)的次数不为1,所以我们可以从(m)中分解出(p)，那么(varphi(p*m) = varphi(m) * p)，否则(varphi(p * m) =varphi(m) * (p-1))。

• 再例如默比乌斯函数(mu)，只有当(k=1)时(mu(p^k)=-1)，否则(mu(p^k)=0)，和欧拉函数一样根据(m)是否被(p)整除判断。

void Linear_Shaker(int N) {
  phi[1] = mu[1] = 1;
  for (int i = 2; i <= N; i++) {
    if (!phi[i]) {
      phi[i] = i - 1;
      mu[i] = -1;
      prime[cnt++] = i;
    }
    for (int j = 0; j < cnt; j++) {
      if (prime[j] * i > N)
        break;
      if (i % prime[j] == 0) {
        phi[i * prime[j]] = phi[i] * prime[j];
        mu[i * prime[j]] = 0;
        break;
      } else {
        phi[i * prime[j]] = phi[i] * (prime[j] - 1);
        mu[i * prime[j]] = -mu[i];
      }
    }
  }
  for (int i = 2; i <= N; i++) {
    phi[i] += phi[i - 1];
    mu[i] += mu[i - 1];
  }
}

3.1.2.5线性筛逆元

令(f(i))为(i)在(mod p)意义下的逆元。显然这个函数是积性函数，我们可以使用线性筛求。但是其实没有那么麻烦。

我们设(p = ki+r)，那么(ki+r equiv 0 (mod p))，两边同时乘(i^{-1}r^{-1})，有(kr^{-1}+i^{-1}equiv 0)，那么(i^{-1} equiv -kr^{-1}=-lfloor frac {p}{i} floor * (p mod i)^{-1})，这样就可以递推了。

void getinv(int n) {
  inv[1] = 1;
  for(int i = 2; i <= x; i++)
    inv[i] = (long long)(p - p/i)*inv[p % i] % p;
}

有了逆元，我们就可以预处理阶乘的逆元

[n!^{-1} equiv prod_{k=1}^n k^{-1} mod p ]

3.1.3默比乌斯反演与狄利克雷卷积

3.1.3.1初等积性函数(mu)

(mu)就是容斥系数。

[mu(n) = egin{cases} 0, & ext{if $exists x^2|n$} \ (-1)^k&n=prod_limits{i=1}^{k}p_i \ end{cases} ]

(mu)函数也是一个积性函数。

下面的公式可以从容斥的角度理解。

[sum_{d|n}mu(d)=[n=1] ]

3.1.3.2默比乌斯反演

首先给出Mobius反演的公式：

[F(n)=sum_{d|n}f(d) Rightarrow f(n)=sum_{d|n}mu(frac{n}{d})F(d) ]

有两种常见的证明，一种是运用Dirichlet卷积，一种是使用初等方法。

证明：

[sum_{d|n}mu(d)F(frac{n}{d}) = sum_{d|n}mu(frac{n}{d})F(d)=sum_{d|n}mu(frac{n}{d})sum_{k|d}f(k)\=sum_{d|n}sum_{k|d}mu(frac{n}{d})f(k)=sum_{k|n}sum_{d|frac{n}{k}}mu(frac{n}{kd})f(k)\ =sum_{k|n}sum_{d|frac{n}{k}}mu(d)f(k)=sum_{k|n}[frac{n}{k} = 1]f(k)=f(n) ]

默比乌斯反演的另一种形式：

[F(n)=sum_{n|d}f(d)Rightarrow f(n)=sum_{n|d}mu(frac{d}{n})F(d) ]

这个式子的证明与上式大同小异，我在这里写一下关键步骤

[sum_{n|d}sum_{d|k}mu(frac{d}{n})f(k)=sum_{n|k}sum_{d|frac{k}{n}}mu(d)f(k)=f(n) ]

对于一些函数(f(n))，如果我们很难直接求出他的值，而容易求出倍数和或者因数和(F(n))，那么我们可以通过默比乌斯反演来求得(f(n))的值

3.1.3.3狄利克雷卷积

定义两个数论函数(f(x)),(g(x))的(Dirichlet)卷积

[(f*g)(n)=sum_{d|n}f(d)g(frac nd) ]

Dirichlet卷积满足交换律，结合律，分配律，单位元。

运用狄利克雷卷积不难证明默比乌斯反演。

3.1.4积性函数求和与杜教筛

3.1.4.1概述

如果能通过狄利克雷卷积构造一个更好计算前缀和的函数，且用于卷积的另一个函数也易计算，则可以简化计算过程。

设(f(n))为一个数论函数，需要计算(S(n)=sum_{i=1}^n f(i))。

根据函数(f(n))的性质，构造一个(S(n))关于(S(lfloor frac ni floor))的递推式，如下例：

找到一個合适的数论函数(g(x))

[sum_{i=1}^nsum_{d|i}f(d)g(frac id)=sum_{i=1}^ng(i)S(lfloorfrac ni floor) ]

可以得到递推式

[g(1)S(n)=sum_{i=1}^n(f*g)(i)-sum_{i=2}^ng(i)S(lfloor frac{n}{i} floor) ]

在递推计算(S(n))的过程中，需要被计算的(S(lfloor frac ni floor))只有(O(sqrt n))种。

3.1.4.1欧拉函数求前缀和

利用(varphi * I=id)的性质，可以有：

[S(n)=sum_{i=1}^ni-sum_{i=2}^nS(lfloor frac ni floor) ]

3.1.4.2默比乌斯函数前缀和

利用(mu * I = e)的性质，可以有：

[S(n)=1-sum_{i=2}^nS(lfloorfrac ni floor) ]

3.1.4.3模板

ll get_p(int x) { return (x <= m) ? phi[x] : p[n / x]; };
ll get_q(int x) { return (x <= m) ? mu[x] : q[n / x]; };
void solve(ll x) {
  if (x <= m)
    return;
  int i, last = 1, t = n / x;
  if (vis[t])
    return;
  vis[t] = 1;
  p[t] = ((x + 1) * x) >> 1;
  q[t] = 1;
  while (last < x) {
    i = last + 1;
    last = x / (x / i);
    solve(x / i);
    p[t] -= get_p(x / i) * (last - i + 1);
    q[t] -= get_q(x / i) * (last - i + 1);
  }
}
//注：本代码为了避免数组过大，p[]和q[]记录的是分母的值。

3.1.5中国剩余定理

中国剩余定理给出了以下的一元线性同余方程组有解的判定条件：

[left{ egin{array}{c} x equiv a_1 pmod {m_1}\ x equiv a_2 pmod {m_2}\ vdots \ x equiv a_n pmod {m_n} end{array} ight. ]

中国剩余定理指出，如果模数两两互质，那么方程组有解，并且通解可以构造得到：

1. 设(M = prod_{i=1}^n m_i)，并设(M_i=frac{M}{m_i})。
2. 设(t_i=M_i^{-1} pmod {m_i})。
3. 那么通解(x = sum_{i=1}^n a_it_iM_i)。

3.1.6高斯消元

Gauss消元法就是使用初等行列式变换把原矩阵转化为上三角矩阵然后回套求解。给定一个矩阵以后，我们考察每一个变量，找到它的系数最大的一行，然后根据这一行去消除其他的行。

double a[N][N]
void Gauss(){
    for(int i=1;i<=n;i++){
        int r=i;
        for(int j=i+1;j<=n;j++)
            if(abs(a[j][i])>abs(a[r][i])) r=j;
        if(r!=i) for(int j=1;j<=n+1;j++) swap(a[i][j],a[r][j]);

        for(int j=i+1;j<=n;j++){
            double t=a[j][i]/a[i][i];
            for(int k=i;k<=n+1;k++) a[j][k]-=a[i][k]*t;
        }
    }
    for(int i=n;i>=1;i--){
        for(int j=n;j>i;j--) a[i][n+1]-=a[j][n+1]*a[i][j];
        a[i][n+1]/=a[i][i];
    }
}

对于xor运算，我们可以使用同样的方法消元。

另外，xor的话可以使用bitset压位以加速求解。

3.1.7大步小步BSGS算法

大步小步算法用于解决：

已知(A,B,C)，求(x)使得, 其中(C is a prime).

[A^xequiv Bpmod C ]

我们令(x=i imes m-frac{j}{m}=lceil sqrt C ceil, i in [1,m], j in [0,m])

那么原式就变成了$$A^{im}=A^j imes B$$ .我们先枚举(j)，把(A^j imes B)加入哈希表，然后枚举(i)，在表中查找(A^{im})，如果找到了，就找到了一个解。时间复杂度为(Theta (sqrt n))。

ll BSGS(ll A, ll B, ll C) {
    mp.clear();
    if(A % C == 0) return -2;
    ll m = ceil(sqrt(C));
    ll ans;
    for(int i = 0; i <= m; i++) {
        if(i == 0) {
            ans = B % C;
            mp[ans] = i;
            continue;
        }
        ans = (ans * A) % C;
        mp[ans] = i;
    }
    ll t = pow(A, m, C); 
    ans = t;
    for(int i = 1; i <= m; i++) {
        if(i != 1)ans = ans * t % C;
        if(mp.count(ans)) {
            int ret = i * m % C - mp[ans] % C;
            return (ret % C + C)%C;
        }
    }
    return -2;
} 

3.2组合数学

3.2.1组合计数与二项式定理

3.2.1.1二项式定理

[（a+b)^n=sum_{i=0}^n C_n^i a^{i}b^{n-i} ]

其中(C_n^m)为二项式系数，满足几个结论：

[C_n^i=C_n^{n-i} ]

[C_{n+1}^m=C_n^m+C_n^{m-1} ]

[sum_{i=0}^nC_n^i=2^n ]

[C_n^k=frac{k}{n}C_{n-1}^{k-1} ]

3.2.1.2排列组合

• 隔板法与插空法

• n元素集合的循环r排列的数目是(frac{P_n^r}r)

• 多重集合全排列$$frac{n!}{prod_i n_i!}$$

• 多重集合的组合，无限重复数，设S是有k种类型对象的多重集合，r组合的个数为$$C_{r+k-1}^r=C_{r+k-1}^{k-1}$$。

• (Lucas)定理(p为素数) ：

  [C_n^m equiv C_{n / p}^{m/p} imes C_{n mod p}^{m mod p} pmod p ]

int C(int n, int m, int P) { 
    if (n < m) return 0;
    return (ll)fac[n] * inv(fac[n-m], P) % P * inv(fac[m], P)%P;
}
int lucas(int n, int m, int P) {
    if(!n && !m) return 1;
    return (ll)lucas(n/P, m/P, P) * C(n%P, m%P, P) % P;
}

3.2.2常见数列

• 错位排列 $$D_n = (n-1) * (D_{n-1} + D_{n-2})$$
• Catanlan数
  [C(n) = sum (C(n-I) * C(I)) ]
  计算公式：
  [C(n) = frac{C(2n,n)}{n+1} ]
  应用：
  满足递推关系的均可表示成catalan数，比如：
  出栈顺序，二叉树种类个数，门票问题，格子问题（不穿过对角线），括号配对问题等等。

3.2.3置换群与(Polya)定理

• (Burnside)引理((Z_k):(k)不动置换类,(c_1(a)):一阶循环的个数:
  [l=frac1{|G|}sum_{k=1}^n|Z_k|=frac1{|G|}sum_{j=1}^gc_1(a_j) ]

• 设置换群G作用于有限集合χ上，用k种颜色涂染集合χ中的元素，则χ在G作用下等价类的数目为((m(f))为置换(f)的循环节)：$$N=frac 1{|G|}sum_{f in G}k^{m(f)}$$

3.2.4容斥原理

[|cup_{i=1}^nA_i|=sum_{i=1}^nA_i-sum_{i,j:i ot=j}|A_i cap A_j|+sum_{i,j,k:i ot=j ot=k}|A_i cap A_j cap A_k|-cdots pm |A_1 cap cdots cap A_n| ]

void calc(){
    for(int i = 1; i < (1 << ct); i++) {
        //do sth
        for(int j = 0; j < ct; j++) {
            if(i & (1 << j)) {
                cnt++;
                //do sth 
            }
        }
        if(cnt & 1) ans += tmp;
        else ans -= tmp;
    }
}

3.3常见结论与技巧

3.3.1裴蜀定理

若a,b是整数,且（a,b)=d，那么对于任意的整数x,y,ax+by都一定是d的倍数，特别地，一定存在整数x,y，使ax+by=d成立。

它的一个重要推论是：a,b互质的充要条件是存在整数x,y使ax+by=1.

3.3.2底和顶

• 若连续且单调增的函数(f(x))满足当(f(x))为整数时可推出(x)为整数，则$$lfloor f(x) floor = lfloor f(lfloor x floor) floor$$和(lceil f(x) ceil = lceil f(lceil x ceil) ceil)

• [lfloor frac {lfloorfrac{x}{a} floor}{b} floor = lfloor frac{x}{ab} floor ]

• 对于(i)，(lfloor frac{n}{lfloor frac{n}{i} floor} floor)是与(i)被(n)除并下取整取值相同的一段区间的右端点

3.3.3和式

3.3.3.1三大定律

• 分配律 $$sum_{k in K} c a_k = c sum_{k in K} a_k$$
• 结合律$$sum_{k in K}(a_k + b_k)=sum_{k in K}a_k+sum_{k in K}b_k$$
• 交换律$$sum_{k in K}a_k=sum_{p(k) in K} a_{p(k)}$$其中p(k)是n的一个排列
• 松弛的交换律:若对于每一个整数(n)，都恰好存在一个整数(k)使得(p(k)=n)，那么交换律同样成立。

3.3.3.2求解技巧

• 扰动法，用于计算一个和式，其思想是从一个未知的和式开始，并记他为(S_n)：$$S_n=sum_{0 leqslant k leqslant n} a_k$$，然后，通过将他的最后一项和第一项分离出来，用两种方法重写(S_{n+1})，这样我们就得到了一个关于(S_n)的方程，就可以得到其封闭形式了。

• 一个常见的交换

  [sum_{d|n}f(d)=sum_{d|n}f(frac{n}{d}) ]

3.3.3.3多重和式

• 交换求和次序：

[sum_jsum_ka_{j,k}[P(j,k)]=sum_{P(j,k)}a_{j,k}=sum_ksum_ja_{j,k}[P(j,k)] ]

• 一般分配律：$$sum_{j in J, k in K}a_jb_k=(sum_{j in J}a_j)(sum_{k in K}b_k)$$

• (Rocky Road)

  [sum_{j in J}sum_{k in K(j)}a_{j,k}=sum_{k in K^{'}}sum_{j in J^{'}}a_{j,k} ]

[[j in J][k in K(j)]=[k in K^{'}][j in J^{'}(k)] ]

事实上，这样的因子分解总是可能的：我们可以设(J=K^{'})是所有整数的集合，而(K(j))和(J^{'}(K))是与操控二重和式的性质(P(j,k))相对应的集合。下面是一个特别有用的分解。

[[1leqslant j leqslant n][j leqslant k leqslant n] = [1 leqslant j leqslant k leqslant n] = [1 leqslant k leqslant n][1 leqslant j leqslant k] ]

• 一个常见的分解

  [sum_{d|n}sum_{k|d}=sum_{k|m}sum_{d|frac{m}{k}} ]

• 一个技巧

  如果我们有一个包含(k+f(j))的二重和式，用(k-f(j))替换(k)并对(j)求和比较好。

3.3.4数论问题的求解技巧

• ({lfloor frac{n}{i} floor|i in [1,n]})只有(O(sqrt n))种取值。所以可以使用这个结论降低复杂度。

例如，在bzoj2301中，我们最终解出了$$f(n, m)=sum_{1 leqslant d leqslant min(n, m)}mu(d)lfloor frac {n}{d} floor lfloor frac {m}{d} floor$$我们就可以使用杜教筛计算出默比乌斯函数的前缀和，计算出商与除以i相同的最多延伸到哪里，下一次直接跳过这一段就好了。下面是这个题的一段程序。

int calc(int n, int m) {
    int ret = 0, last;
    if(n > m) std::swap(n, m);
    for(int i = 1; i <= n; i = last + 1) { //i就相当于原式中的d
        last = min(n / (n/i), m / (m/i));  //last计算了商与除以i相同的最多延伸到哪里，不难证明这样计算的正确性
        ret += (n / i) * (m / i) * (sum[last] - sum[i-1]);
    }
    return ret;
}

3.3.5一些可能会用到的定理

3.3.5.1费马小定理

[a^{p-1}equiv1pmod p ]

条件：(p is prime and (a,p)=1)

3.3.5.2欧拉定理

[a^{varphi(p)}equiv 1pmod p ]

条件：(a,p in mathbb{Z^+}, (a, p)=1)

3.3.5.3威尔逊定理

[(p-1)!equiv-1pmod p Leftrightarrow p is prime ]

3.3.5.4皮克定理

[S=n+frac s2-1 ]

(其中(n)表示多边形内部的点数,(s)表示多边形边界上的点数,(S)表示多边形的面积)

3.4其他数学工具

3.4.1快速乘

inline ll mul(ll a, ll b) {
  ll x = 0;
  while (b) {
    if (b & 1)
      x = (x + a) % p;
    a = (a << 1) % p;
    b >>= 1;
  }
  return x;
}

3.4.2快速幂

inline ll pow(ll a, ll b, ll p) {
  ll x = 1;
  while (b) {
    if (b & 1)
      x = mul(x, a);
    a = mul(a, a);
    b >>= 1;
  }
  return x;
}

3.4.3更相减损术

第一步：任意给定两个正整数；判断它们是否都是偶数。若是，则用2约简；若不是则执行第二步。

第二步：以较大的数减较小的数，接着把所得的差与较小的数比较，并以大数减小数。继续这个操作，直到所得的减数和差相等为止。

则第一步中约掉的若干个2与第二步中等数的乘积就是所求的最大公约数。

3.4.4逆元

根据费马小定理(p是质数)，

int inv(int x, int P){return pow(x, P-2, P);}

或使用扩展欧几里德:

int inv(int x, int P) {
  int d, a, b;
  gcd(x, P, d, a, b);
  return d == 1 ? (a+P)%P : -1;
}

3.4.5博弈论

• Nim游戏
• SG函数

定义$$SG(x)=mex(S)$$，其中(S)是(x)的后继状态的(SG)函数集合，(mex(S))表示不在(S)内的最小非负整数。

• SG定理

组合游戏和的(SG)函数等于各子游戏(SG)函数的(Nim)和。

3.4.6概率与数学期望

• 全概率公式$$P(A)=P(A|B_1)P(B_1)+P(A|B_2)P(B_2)+cdots+P(A|B_n)*P(B_n)$$
• 数学期望

3.4.7快速傅立叶变换

3.4.7.1基本定义

快速傅立叶变换(FFT)用于求解多项式的卷积.

• 单位根:单位圆的(n)等分点为终点,作(n)个向量,所得的幅角为正且最小的向量对应的复数为(omega_n),称为(n)次单位根.
  [omega_n^k=coskfrac{2pi}{n}+isin kfrac{2pi}n ]

• 单位根的性质:$$omega_{2n}^{2k}=omega_n^k$$
• 单位根的性质:$$omega_{n}^{k+frac nk}=-omega _n^k$$

3.4.7.2快速傅立叶变换

考虑将多项式(A_1(x)=a_0+a_2x^2+a_4x^4+cdots+a_{n-2}x^{frac n2 -1})

[A_2(x)=a_1+a_3x+a_5x^2+cdots+a_{n-1}x^{frac n2 -1} ]

则有$$A(x)=A_1(x)+xA_2(x)$$

有$$A(omega_n^k)=A_1(omega_n^{2k})+omega_n^kA_2(omega_n^{2k})$$

有$$A(omega_n^{k+frac n2})=A_1{omega_frac n2^k-omega_n^kA_2(omega_frac n2 ^ k)}$$.

注意到,当(k)取遍([0,frac n2 -1])时,(k)和(k+frac n2)取遍了([0,n-1]),也就是说，如果已知(A_1(x))和(A_2(x))在(omega_{n/2}^0,omega_{n/2}^1,cdots,omega_{n/2}^{n/2-1})处的点值，就可以在(O(n))的时间内求得(A(x))在(omega_n^0,omega_n^1,cdots,omega_n^{n-1})处的取值。而关于 (A_1(x)) 和 (A_2(x)) 的问题都是相对于原问题规模缩小了一半的子问题，分治的边界为一个常数项(a_0).

该算法的复杂度为(O(nlogn)).

3.4.7.3傅立叶逆变换

设((y_0,y_1,cdots,y_{n-1}))为((a_0,cdots,a_{n-1}))的快速傅立叶变换. 考虑另一个向量((c_0,cdots,c_{n-1}))满足

[c_k=sum_{i=0}^{n-1}y_i(omega_n^{-k})^i$$. 即多项式$B(x)=y_0+y_1x+cdots+y_{n-1}x^{n-1}$在$omega_n^0,cdots,omega_n^{-(n-1)}$处的点值表示. 可以得到(证明略) $$a_i=frac 1n c_i$$. 所以，使用单位根的倒数代替单位根，做一次类似快速傅里叶变换的过程，再将结果每个数除以$n$，即为傅里叶逆变换的结果。 ##### 3.7.4.4代码实现 FFT有两种常见的代码实现: 递归版本和迭代版本,一般来讲递归效率很差,但由于我非常菜,一轮省选就先使用递归版本骗分.迭代版本以后会更新. ```c++ const double PI = acos(-1); bool inversed = false; inline std::complex<double> omega(const int n, const int k) { if (!inversed) return std::complex<double>(cos(2 * PI / n * k), sin(2 * PI / n * k)); else return std::conj( std::complex<double>(cos(2 * PI / n * k), sin(2 * PI / n * k))); } void fft(std::complex<double> *a, std::complex<double> *ans, int n) { if (n == 1) { ans[0] = a[0]; return; } std::complex<double> buf[maxn]; int m = n >> 1; for (int i = 0; i < m; i++) { buf[i] = a[i * 2]; buf[i + m] = a[i * 2 + 1]; } std::complex<double> tmp[maxn]; fft(buf, tmp, m); fft(buf + m, tmp + m, m); for (int i = 0; i < m; i++) { std::complex<double> x = omega(n, i); ans[i] = tmp[i] + x * tmp[i + m]; ans[i + m] = tmp[i] - x * tmp[i + m]; } } void solve() { //sth while (N < n + 1) N <<= 1; N <<= 1; fft(a, ans1, N); fft(b, ans2, N); std::complex<double> ans3[maxn]; for (int i = 0; i < N; i++) ans3[i] = ans1[i] * ans2[i]; std::complex<double> tmp[maxn]; inversed = true; fft(ans3, tmp, N); for (int i = 0; i < N; i++) c[i] = tmp[i].real() / N; //sth } ``` $mathtt{COPYRIGHT}© mathtt{2017,KONJAC,MIT LICENSE} $]