https://blog.csdn.net/u013709270/article/details/78275462
1. 统计学习方法都是由模型，策略，和算法构成的，即统计学习方法由三要素构成，可以简单表示为：
方法=模型+策略+算法
对于logistic回归来说，模型自然就是logistic回归，策略最常用的方法是用一个损失函数(loss function)或代价函数(cost function)来度量预测错误程度，算法则是求解过程，后期会详细描述相关的优化算法。
2.常见的损失函数
机器学习或者统计机器学习常见的损失函数如下：
1.0-1损失函数 （0-1 loss function）
2.感知损失（Perceptron Loss）
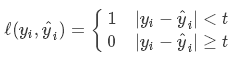
其中t是一个超参数阈值，如在PLA(Perceptron Learning Algorithm,感知机算法)中取t=0.5。
3.Hinge Loss
Hinge损失可以用来解决间隔最大化问题，如在SVM中解决几何间隔最大化问题，其定义如下：
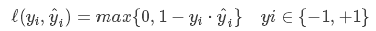
更多请参见：Hinge-loss。
4.平方损失函数（quadratic loss function)
L(Y,f(X))=(Y−f(x))2
5.绝对值损失函数(absolute loss function)
L(Y,f(x))=|Y−f(X)|
6.对数损失函数（logarithmic loss function) 或对数似然损失函数(log-likehood loss function)
L(Y,P(Y|X))=−logP(Y|X)
在使用似然函数最大化时，其形式是进行连乘，为了便于处理，一般会套上log，这样便可以将连乘转化为求和，由于log函数是单调递增函数，因此不会改变优化结果。因此log类型的损失函数也是一种常见的损失函数，如在LR(Logistic Regression, 逻辑回归)中使用交叉熵(Cross Entropy)作为其损失函数；损失函数越小，表示模型越好。即：
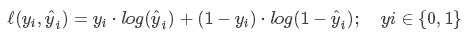（注：前面需要加个负号。这里log为自然对数ln）
规定： 0⋅log(0)=0
7.指数损失函数（Exponential Loss）
常用于boosting算法中，如AdaBoost。即：
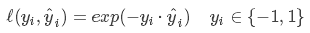
3.对过拟合和加入正则化项防止过拟合的直观理解：
1.过拟合从直观上理解便是，在对训练数据进行拟合时，需要照顾到每个点，从而使得拟合函数波动性非常大，即方差大。在某些小区间里，函数值的变化性很剧烈，意味着函数在某些小区间里的导数值的绝对值非常大，由于自变量的值在给定的训练数据集中的一定的，因此只有系数足够大，才能保证导数的绝对值足够大。如下图：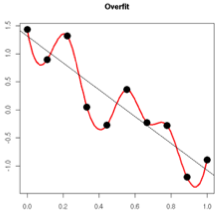
加入正则化项，通过限制系数不能过大，就可以使得函数值的变化不至于在小区间很剧烈；即增加了一部分偏差，但减少了方差，防止了或许因异常点和噪点造成的过拟合。
2.
另外一个解释，规则化项的引入，在训练（最小化cost）的过程中，当某一维的特征所对应的权重过大时，而此时模型的预测和真实数据之间距离很小，通过规则化项就可以使整体的cost取较大的值，从而，在训练的过程中避免了去选择那些某一维（或几维）特征的权重过大的情况，即避免过分依赖某一维（或几维）的特征。
4.L2与L1正则化的区别
L1正则是拉普拉斯先验，而L2正则则是高斯先验。它们都是服从均值为0，协方差为1λ。当λ=0时，即没有先验）没有正则项，则相当于先验分布具有无穷大的协方差，那么这个先验约束则会非常弱，模型为了拟合所有的训练集数据， 参数w可以变得任意大从而使得模型不稳定，即方差大而偏差小。λ越大，标明先验分布协方差越小，偏差越大，模型越稳定。即，加入正则项是在偏差bias与方差variance之间做平衡tradeoff。下图即为L2与L1正则的区别：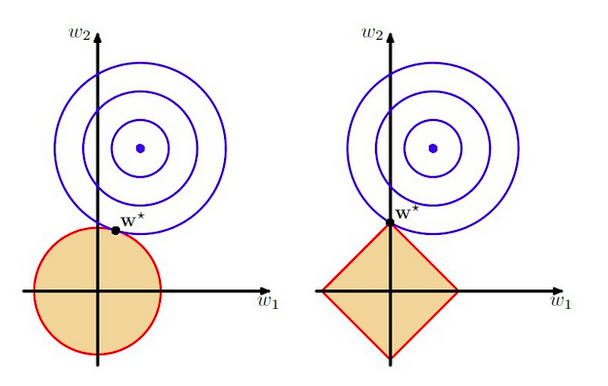
上图中的模型是线性回归，有两个特征，要优化的参数分别是w1和w2，左图的正则化是L2，右图是L1。蓝色线就是优化过程中遇到的等高线，一圈代表一个目标函数值，圆心就是样本观测值（假设一个样本），半径就是误差值，受限条件就是红色边界（就是正则化那部分），二者相交处，才是最优参数。可见右边的最优参数只可能在坐标轴上，所以就会出现0权重参数，使得模型稀疏。
一个疑问：L1正则化中，相切的地方，w1和w2也可以都不为0；比如当等高线的圆心位于y=x直线上时。的确如此，但圆心刚好在y=x直线上的情况非常少；或者说这些情况下对应的就是那些不会被缩减太多的重要参数。大多在其他地方，这样相交的点是坐标轴上的点；对应的就是那些不重要的被缩减或被删减的点。
5.Logistics回归采用“损失函数最小化求参数”与“极大似然估计联合概率最大化求参数”之间的关系
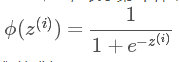ϕ(z)可以视为类1的后验估计，所以我们有：
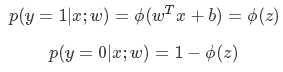
其中，p(y=1|x;w)表示给定w，那么x点y=1的概率大小。 于是上面两式可以写成一般形式：
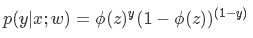
先用极大似然估计来根据给定的训练集估计出参数w：
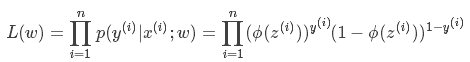
为了简化运算，我们对上面这个等式的两边都取一个对数：
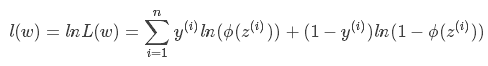
我们现在要求的是使得l(w)最大的w。而在l(w)前面加个负号就是求使得l(w)最小的w了，这就是Logistics回归的损失函数：
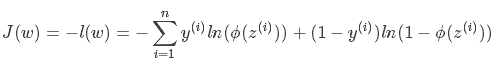
以上的过程说明：Logistics回归采用“损失函数最小化求参数”与“极大似然估计联合概率最大化求参数”是完全等价的！这就是为什么Logistics回归中激活函数使用sigmoid函数，损失函数使用-log损失函数的原因。Logistics回归的参数可以采用最大似然函数进行估计。
6.梯度下降中，为何梯度的负方向就是代价函数下降最快的方向（证明如下）
首先：
其中，f′(x)和δ为向量，那么这两者的内积就等于 :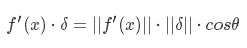 
当θ=π时，也就是δ在f′(x)的负方向上时，取得最小值，也就是下降的最快的方向了。
7.LR回归损失函数对各个参数θ的推导:https://blog.csdn.net/zrh_CSDN/article/details/80934278
Logistics回归与线性回归对各个参数的梯度值（求偏导）表达式完全相同
推导的结果发现：LR回归采用-log损失函数对各个参数θ的偏导值，和 线性回归采用均方误差损失函数对各个参数θ的偏导值，所得的偏导公式是完全一样的
所以采用梯度下降求解参数时，方法是一样的