tarjan陪伴强联通分量
生成树完成后思路才闪光
欧拉跑过的七桥古塘
让你 心驰神往”----《膜你抄》
自从听完这首歌,我就对tarjan开始心驰神往了,不过由于之前水平不足,一直没有时间学习。这两天好不容易学会了,写篇博客,也算记录一下。
一、tarjan求强连通分量
1、什么是强连通分量?
引用来自度娘的一句话:
“有向图强连通分量:在有向图G中,如果两个顶点vi,vj间(vi>vj)有一条从vi到vj的有向路径,同时还有一条从vj到vi的有向路径,则称两个顶点强连通(strongly connected)。如果有向图G的每两个顶点都强连通,称G是一个强连通图。有向图的极大强连通子图,称为强连通分量(strongly connected components)。”
一脸懵逼......不过倒也不难理解。
反正就是在图中找到一个最大的图,使这个图中每个两点都能够互相到达。这个最大的图称为强连通分量,同时一个点也属于强连通分量。
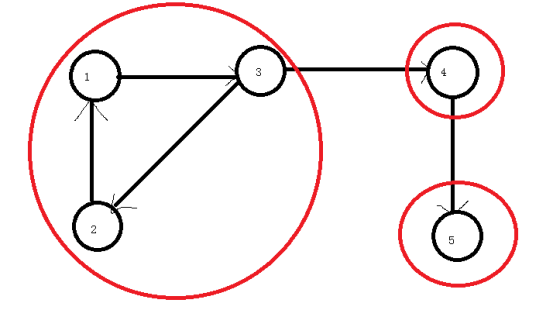
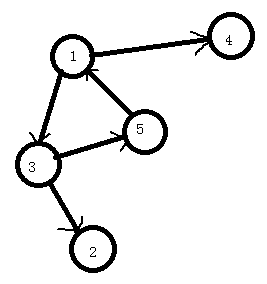
如图中强连通分量有三个:1-2-3,4,5
2、强连通分量怎么找?
噫......当然,通过肉眼可以很直观地看出1-2-3是一组强连通分量,但很遗憾,机器并没有眼睛,所以该怎么判断强连通分量呢?
如果仍是上面那张图,我们对它进行dfs遍历。
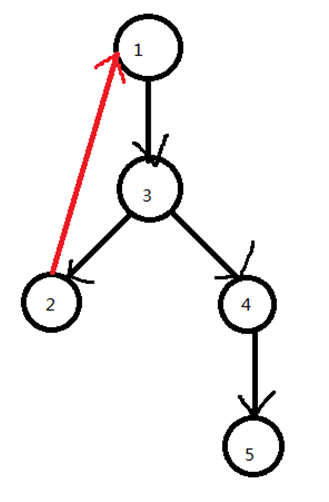
可以注意到红边非常特别,因为如果按照遍历时间来分类的话,其他边都指向在自己之后被遍历到的点,而红边指向的则是比自己先被遍历到的点。
如果存在这么一条边,那么我们可以yy一下,emmmm.......
从一个点出发,一直向下遍历,然后忽得找到一个点,那个点竟然有条指回这一个点的边!
那么想必这个点能够从自身出发再回到自身
想必这个点和其他向下遍历的该路径上的所有点构成了一个环,
想必这个环上的所有点都是强联通的。
但只是强联通啊,我们需要求的可是强连通分量啊......
那怎么办呢?
我们还是yy出那棵dfs树
不妨想一下,什么时候一个点和他的所有子孙节点中的一部分构成强连通分量?
他的子孙再也没有指向他的祖先的边,却有指向他自己的边
因为只要他的子孙节点有指向祖先的边,显然可以构成一个更大的强联通图。
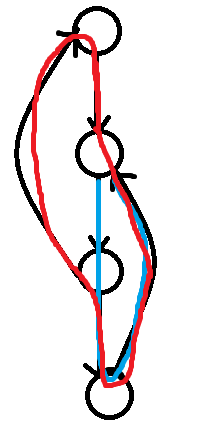
比如说图中红色为强连通分量,而蓝色只是强联通图
那么我们只需要知道这个点u下面的所有子节点有没有连着这个点的祖先就行了。
但似乎还有一个问题啊......
我们怎么知道这个点u它下面的所有子节点一定是都与他强联通的呢?
这似乎是不对的,这个点u之下的所有点不一定都强联通
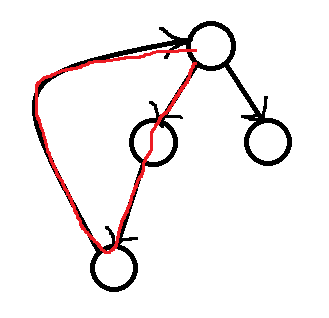
那么怎么在退回到这个点的时候,知道所有和这个点u构成强连通分量的点呢?
开个栈记录就行了
什么?!这么简单?
没错~就是这么简单~
如果在这个点之后被遍历到的点已经能与其下面的一部分点(也可能就只有他一个点)已经构成强连通分量,即它已经是最大的。
那么把它们一起从栈里弹出来就行了。
所以最后处理到点u时如果u的子孙没有指向其祖先的边,那么它之后的点肯定都已经处理好了,一个常见的思想,可以理解一下。
所以就可以保证栈里留下来u后的点都是能与它构成强连通分量的。
似乎做法已经明了了,用程序应该怎么实现呢?
所以为了实现上面的操作,我们需要一些辅助数组
(1)、dfn[ ],表示这个点在dfs时是第几个被搜到的。
(2)、low[ ],表示这个点以及其子孙节点连的所有点中dfn最小的值
(3)、stk[ ],表示当前所有可能能构成是强连通分量的点。
(4)、onstk[ ],表示一个点是否在stack[ ]数组中。
那么按照之上的思路,我们来考虑这几个数组的用处以及tarjan的过程。
假设现在开始遍历点u:
(1)、首先初始化dfn[u]=low[u]=第几个被dfs到
dfn可以理解,但为什么low也要这么做呢?
因为low的定义如上,也就是说如果没有子孙与u的祖先相连的话,dfn[u]一定是它和它的所有子孙中dfn最小的(因为它的所有子孙一定比他后搜到)。
(2)、将u存入stk[ ]中,并将onstk[u]设为true
stk[ ]有什么用?
如果u在stack中,u之后的所有点在u被回溯到时u和栈中所有在它之后的点都构成强连通分量。
(3)、遍历u的每一个能到的点,如果这个点dfn[ ]为0,即仍未访问过,那么就对点v进行dfs,然后low[u]=min{low[u],low[v]}
low[ ]有什么用?
应该能看出来吧,就是记录一个点它最大能连通到哪个祖先节点(当然包括自己)
如果遍历到的这个点已经被遍历到了,那么看它当前有没有在stack[ ]里,如果有那么low[u]=min{low[u],low[v]}
如果已经被弹掉了,说明无论如何这个点也不能与u构成强连通分量,因为它不能到达u
如果还在栈里,说明这个点肯定能到达u,同样u能到达他,他俩强联通。
(4)、假设我们已经dfs完了u的所有的子树那么之后无论我们再怎么dfs,u点的low值已经不会再变了。
那么如果dfn[u]=low[u]这说明了什么呢?
再结合一下dfn和low的定义来看看吧
dfn表示u点被dfs到的时间,low表示u和u所有的子树所能到达的点中dfn最小的。
这说明了u点及u点之下的所有子节点没有边是指向u的祖先的了,即我们之前说的u点与它的子孙节点构成了一个最大的强连通图即强连通分量
此时我们得到了一个强连通分量,把所有的u点以后压入栈中的点和u点一并弹出,将它们的vis[ ]置为false,如有需要也可以给它们打上相同标记(同一个数字)
二、tarjan缩点
其实这也是利用了tarjan求强连通分量的方法,对于一些贡献具有传导性,比如友情啊、路径上的权值啊等等。
思想就是因为强连通分量中的每两个点都是强连通的,可以将一个强连通分量当做一个超级点,而点权按题意来定。
我们来看一道题 受欢迎的牛
【代码实现】
1 #include<cstdio> 2 #include<algorithm> 3 #include<cctype> 4 #include<vector> 5 #include<stack> 6 using namespace std; 7 void read(int &x) 8 { 9 int f;char ch; 10 while(!isdigit(ch=getchar())&&ch!='-'); ch=='-'?(x=0,f=-1):(x=ch-'0',f=1); 11 while(isdigit(ch=getchar())) x=x*10+ch-'0'; 12 } 13 const int N=1e4+5; 14 const int M=5e4+5; 15 const int INF=1e9+7; 16 struct sd{ 17 int to,next; 18 }edge[M]; 19 int head[N],dfn[N],low[N],belong[N],fa[N],cnt,bccnt,n,m,ans; 20 bool onstk[N]; 21 vector<int> bcc[N]; 22 stack<int> stk; 23 int find(int v) {if(fa[v]!=v) return fa[v]=find(fa[v]);return fa[v];} 24 void add_edge(int from,int to) 25 { 26 edge[++cnt].next=head[from]; 27 edge[cnt].to=to; 28 head[from]=cnt; 29 } 30 void tarjan(int v) 31 { 32 dfn[v]=low[v]=++cnt,onstk[v]=1,stk.push(v); 33 for(int i=head[v];i;i=edge[i].next) 34 { 35 int to=edge[i].to; 36 if(!dfn[to]) 37 { 38 tarjan(to); 39 low[v]=min(low[to],low[v]); 40 } 41 else if(low[v]>dfn[to]&&onstk[to]) 42 low[v]=dfn[to]; 43 } 44 if(dfn[v]==low[v]) 45 { 46 ++bccnt; 47 while(1) 48 { 49 int node=stk.top();stk.pop(); 50 bcc[bccnt].push_back(node),onstk[node]=0,belong[node]=bccnt; 51 if(node==v) break; 52 } 53 } 54 } 55 int main() 56 { 57 int from,to; 58 read(n),read(m); 59 for(int i=1;i<=n;i++) fa[i]=i; 60 while(m--) 61 { 62 read(from),read(to),add_edge(from,to); 63 int ffa=find(from),ffb=find(to); 64 if(ffa!=ffb) fa[ffb]=ffa; 65 }cnt=0; 66 for(int i=1;i<n;i++) if(find(i)!=find(i+1)) {printf("0 ");return 0;} 67 for(int i=1;i<=n;i++) if(!dfn[i]) tarjan(i); cnt=0; 68 for(int i=1;i<=bccnt;i++) 69 { 70 int out=0; 71 for(int j=bcc[i].size()-1;j>=0;j--) 72 { 73 int gg=bcc[i][j]; 74 for(int k=head[bcc[i][j]];k;k=edge[k].next) 75 if(belong[edge[k].to]!=i) out++; 76 } 77 if(out==0) cnt++,ans=bcc[i].size(); 78 } 79 if(cnt>1) printf("0"); 80 else printf("%d",ans); 81 return 0; 82 }