Floyd算法
使用条件
可以求出多源最短路,可以处理负权边的情况,但是不能出现负环。
时间复杂度
O(n3)
讲解
Floyed算法使用的是动态规划的方法。
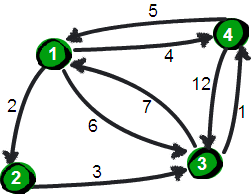
我们首先观察上图。
我们来想一想,根据我们以往的经验,如果要让任意两点(例如从顶点a点到顶点b)之间的路程变短,只能引入第三个点(顶点k),并通过这个顶点k中转即a->k->b,才可能缩短原来从顶点a点到顶点b的路程。那么这个中转的顶点k是1~n中的哪个点呢?甚至有时候不只通过一个点,而是经过两个点或者更多点中转会更短,即a->k1->k2b->或者a->k1->k2…->k->i…->b。比如上图中从4号城市到3号城市(4->3)的路程e[4][3]原本是12。如果只通过1号城市中转(4->1->3),路程将缩短为11(e[4][1]+e[1][3]=5+6=11)。其实1号城市到3号城市也可以通过2号城市中转,使得1号到3号城市的路程缩短为5(e[1][2]+e[2][3]=2+3=5)。所以如果同时经过1号和2号两个城市中转的话,从4号城市到3号城市的路程会进一步缩短为10。通过这个的例子,我们发现每个顶点都有可能使得另外两个顶点之间的路程变短。好,下面我们将这个问题一般化。
当任意两点之间不允许经过第三个点时,这些城市之间最短路程就是初始路程,如下。
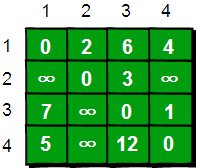
我们如果在每两个点之间设置一个中转点,看看是使用这个中转点之前路程更短还是使用之后路程更短,而两个点到中转点的距离都已经是最短路程,这样最后计算出来的就一定是最短路程了。
只需要使用最简单粗暴的做法,将出发点、结束点、中转点都枚举一遍就可以了。
状态转移方程:
d[i][j]=min(d[i][k]+d[k][j],d[i][j])
这样,再写出Floyd算法的核心代码就很容易了。
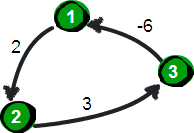
另外需要注意的是:Floyd算法不能解决带有“负权回路”(或者叫“负权环”)的图,因为带有“负权回路”的图没有最短路。例如下面这个图就不存在1号顶点到3号顶点的最短路径。因为1->2->3->1->2->3->…->1->2->3这样路径中,每绕一次1->-2>3这样的环,最短路就会减少1,永远找不到最短路。其实如果一个图中带有“负权回路”那么这个图则没有最短路。
核心代码
for(k=1;k<=n;k++) //枚举中转点 for(i=1;i<=n;i++) //枚举起点 for(j=1;j<=n;j++) //枚举终点 d[i][j]=min(d[i][k]+d[k][j],d[i][j]);
Dijkstra算法
使用条件
求单源最短路径,不能处理负权。
时间复杂度
O(n2)
讲解
Dijkstra算法使用的是贪心方法,d[i]表示起点s0到i的最短距离。
从起点s0开始,选择未访问过的离s0最近的一个点i,也就是最小的d[i],因为所以边权为正,不会存在更短的路径到达i,保证了贪心的正确性。然后将i作为中间点,更新经过i可到达的点的最短路距离,继续贪心寻找未访问过的最近的一个点,经过n次贪心,算法结束。
看图:

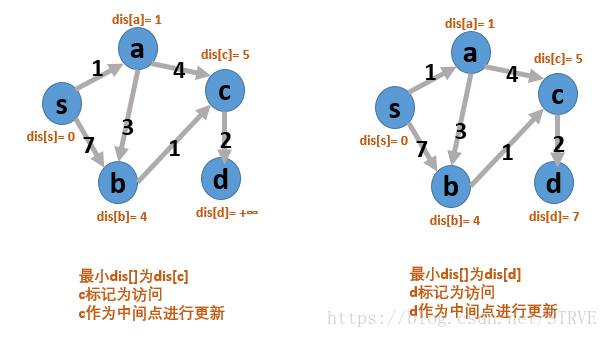
根据这个图,Dijkstra算法应该就很好理解了。
核心代码
for (i = 1; k <= n; k++) { maxn = 0x7fffffff; for (j = 1; j <= n; j++) //找出未访问最小的d[j] { if (!vis[j] && d[j] < maxn) { maxn = d[j]; k = i; } } vis[k] = 1; for (j = 1; j <= n; j++) //k作为中间点,更新起点经过k到达其他点的d[j] if (w[k][j]) { d[j] = min{ d[k] + w[k][j],d[j] }; } }
SPFA算法
使用条件
求单源最短路,可以处理负权边
时间复杂度
对于稀疏图,为O(km),k为较小的常数,而对于稠密图或者构造的网格图,会提高到O(n*m)
讲解
建立一个队列,初始时队列里只有起始点,在建立一个表格记录起始点到所有点的最短路径(该表格的初始值要赋为极大值,该点到他本身的路径赋为0)。然后执行松弛操作,用队列里有的点去刷新起始点到所有点的最短路,如果刷新成功且被刷新点不在队列中则把该点加入到队列最后。重复执行直到队列为空。
图:
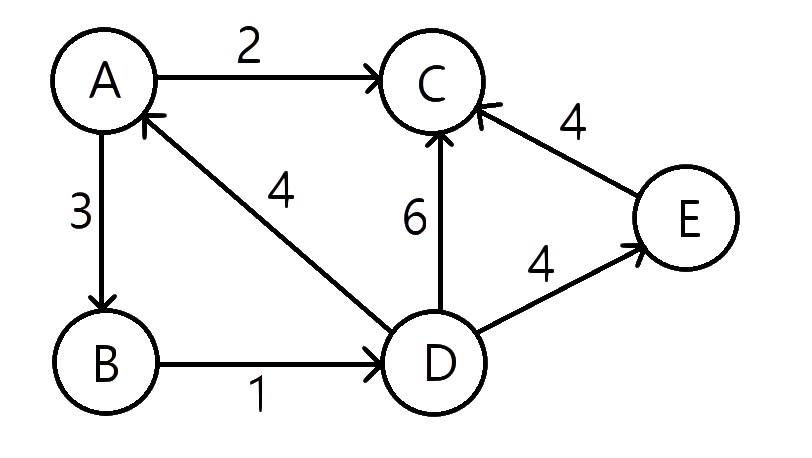
源点A首先入队,并且AB松弛
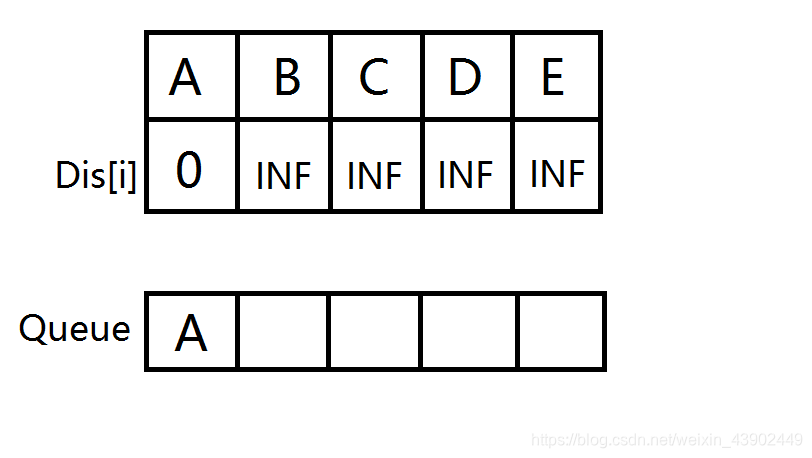
扩展与A相连的边,B,C 入队并松弛。
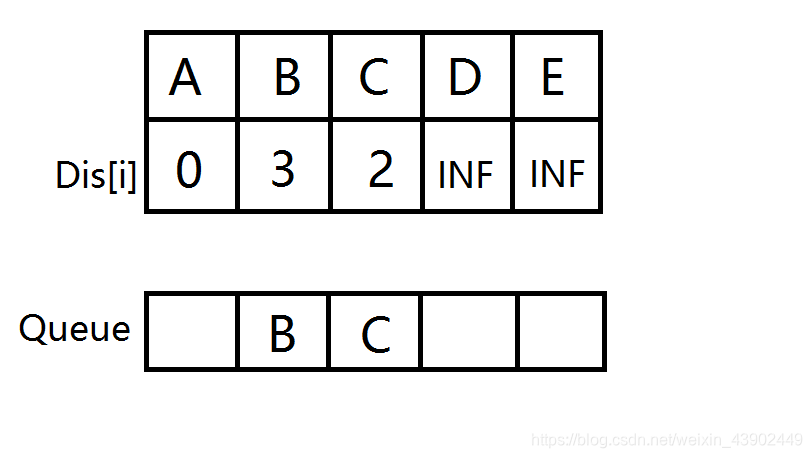
B,C分别开始扩展,D入队并松弛
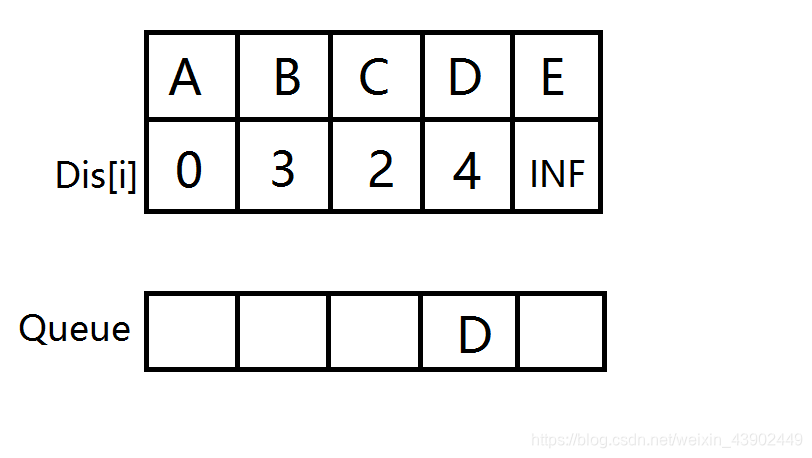
D出队,E入队并松弛。
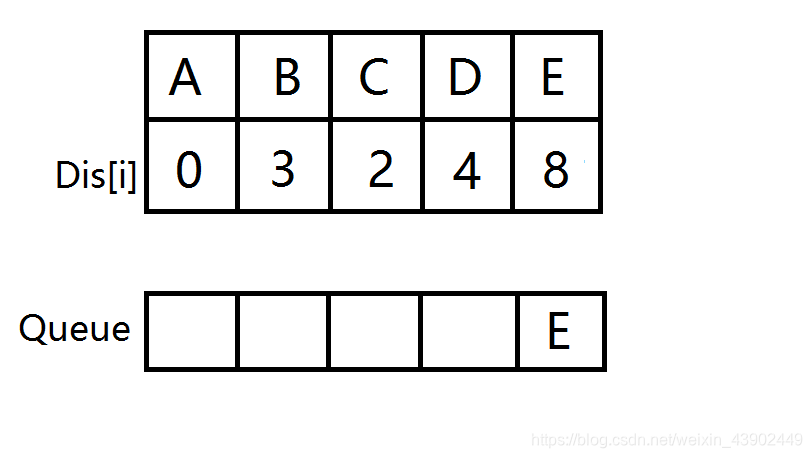
E出队,此时队列为空,源点到所有点的最短路已被找到,A->E的最短路即为8
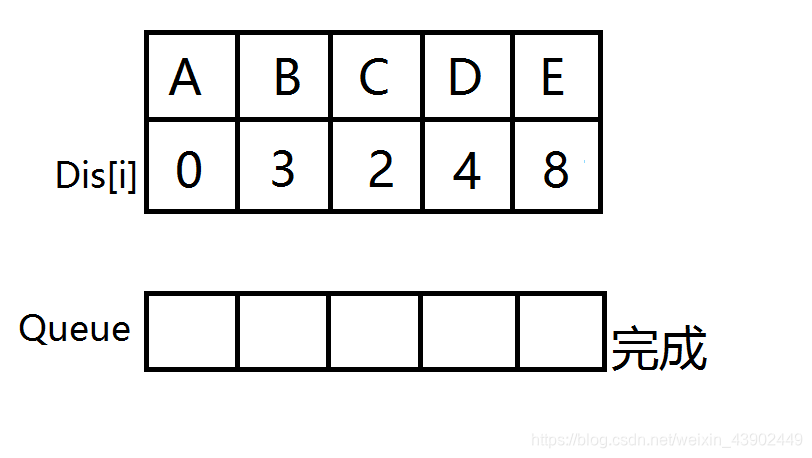
以上就是SPFA算法的过程。
核心代码
q.push(s); vis[s]=1; //源点s入队,标记入队 while(q.size()) { u=q.front();q.pop();vis[u]=0; //取出队头,标记未入队 for(i=head[u];i;i=next[i]) { v=ver[i]; w=edge[i]; if(dis[u]+w<dis[v]) { dis[v]=dis[u]+w; if(!vis[v]) {q.push(v);vis[v]=1;} //如果没有在队列,入队,标记已入队 } } }