题目描述
策策同学特别喜欢逛公园。公园可以看成一张N个点M条边构成的有向图,且没有 自环和重边。其中1号点是公园的入口,N号点是公园的出口,每条边有一个非负权值, 代表策策经过这条边所要花的时间。
策策每天都会去逛公园,他总是从1号点进去,从N号点出来。
策策喜欢新鲜的事物,它不希望有两天逛公园的路线完全一样,同时策策还是一个 特别热爱学习的好孩子,它不希望每天在逛公园这件事上花费太多的时间。如果1号点 到N号点的最短路长为d,那么策策只会喜欢长度不超过d+K的路线。
策策同学想知道总共有多少条满足条件的路线,你能帮帮它吗?
为避免输出过大,答案对P取模。
如果有无穷多条合法的路线,请输出−1。
输入格式
第一行包含一个整数 T, 代表数据组数。
接下来T组数据,对于每组数据: 第一行包含四个整数 N,M,K,,每两个整数之间用一个空格隔开。
接下来M行,每行三个整数\(a_i,b_i,c_i\),代表编号为\(a_i,b_i\)的点之间有一条权值为 \(c_i\)的有向边,每两个整数之间用一个空格隔开。
输出格式
输出文件包含 T行,每行一个整数代表答案。
输入输出样例
输入 #1
2
5 7 2 10
1 2 1
2 4 0
4 5 2
2 3 2
3 4 1
3 5 2
1 5 3
2 2 0 10
1 2 0
2 1 0
输出 #1
3
-1
说明/提示
【样例解释1】
对于第一组数据,最短路为 3。 1–5,1–2–4–5,1–2–3–5为 3 条合法路径。
【测试数据与约定】
对于不同的测试点,我们约定各种参数的规模不会超过如下
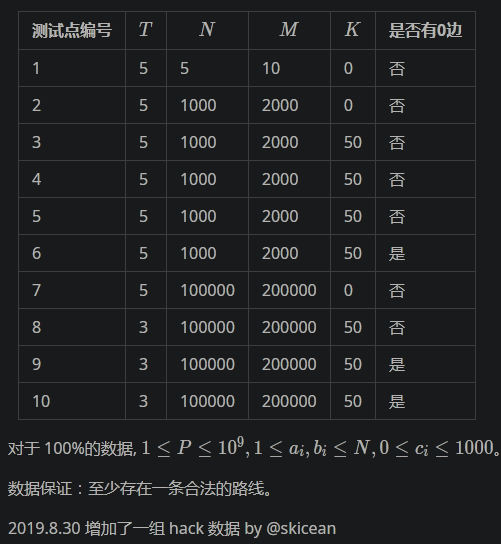
这个题,我们可能会想到求一遍最短路,然后直接暴力统计合法的路线数(当然了这特定会TLE啊)。
那我们考虑怎么优化。
一开始肯定要求一遍最短路,但我们需要的是处理出从n到所有点的路径。
也就是建反向边跑最短路(至于为什么呢,下面会提到的)。
我们首先考虑无解的情况。
当存在一个零环的时候,就说明无解了。
那有解的情况呢?
我们可以对暴力搜索优化一下,变为记忆化搜索。
我们用rest表示当前还能比最短路多走多少
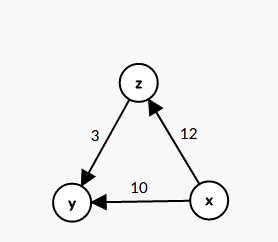
如上图所示,y点为n号点,x为1号点
那么从x-z-y比从x-y的最短路多走了 dis[y]+e[i].w - dis[x]的距离(这也是我们为什么要建反边跑最短路)
那么我们就可以得出经过每条边时多走的距离。
接着往下搜就可以了,如果当前多走的距离要比rest大,说明此条方案不行
若到n点之后,rest >0说明我们找到一条合法的路线,这时候直接往回推就可以了
设 f[i][j] 为比 dis[i] 正好多 j 为长度的方案总数
假设有一条从 p 到 now 长度为 w 的一条边
目标:将 f[now][k] 转移到 f[p][x] ( k 为比最短路多出的长度)
可以发现只有 x 是不知道的量。
可以得出 x−k=dis[p]−dis[now]+w
再将 k 移过去
x=dis[p]+w-dis[now]+k
dp方程就是
f[p][x]=(f[p][x]+f[now][k]) mod p
记忆化搜索就完事了
不懂得同学下面有带注释的代码QAQ
代码
#include<iostream>
#include<cstdio>
#include<algorithm>
#include<cstring>
#include<queue>
using namespace std;
const int N = 1e5+10;
int n,m,T,k,p,tot = 0,u,v,w,sum = 0;
int head[N],dis[N],f[N][59],hed[N];
bool vis[N][59],in[N];
struct node{int to,net,w;}e[200010],edge[200010];
priority_queue<pair<int,int>, vector<pair<int,int> >, greater< pair<int,int> > >q;
inline int read()
{
int s = 0,w = 1; char ch = getchar();
while(ch < '0' || ch > '9'){if(ch == '-') w = -1; ch = getchar();}
while(ch >= '0' && ch <= '9'){s = s * 10+ch -'0'; ch = getchar();}
return s * w;
}
void add(int x,int y,int w)
{
e[++tot].w = w;
e[tot].to = y;
e[tot].net = head[x];
head[x] = tot;
edge[++sum].w = w;
edge[sum].to = x;
edge[sum].net = hed[y];
hed[y] = sum;
}
void chushihua()
{
tot = 0, sum = 0;
memset(head,0,sizeof(head));
memset(vis,0,sizeof(vis));
memset(f,0,sizeof(f));
memset(hed,0,sizeof(hed));
memset(dis,0x3f3f,sizeof(dis));
memset(in,0,sizeof(in));
}
void dij()//在反向图上跑最短路
{
q.push(make_pair(0,n)); dis[n] = 0;
while(!q.empty())
{
int t = q.top().second; q.pop();
if(in[t]) continue;
in[t] = 1;
for(int i = hed[t]; i; i = edge[i].net)
{
int to = edge[i].to;
if(dis[to] > dis[t] + edge[i].w)
{
dis[to] = dis[t] + edge[i].w;
q.push(make_pair(dis[to],to));
}
}
}
}
int dfs(int x,int rest)//记忆化搜索,rest表示当前还能比最短路多走的距离
{
if(vis[x][rest]) return -1; //判0环
if(f[x][rest]) return f[x][rest];//记忆化搜索
if(x == n) f[x][rest] = 1;//到达n点,说明找到一条可行的方案数
vis[x][rest] = 1;//打个标记
for(int i = head[x]; i; i = e[i].net)
{
int to = e[i].to;
int tmp = dis[to] + e[i].w - dis[x];//计算走这条边要比走最短路多经过的距离
if(rest - tmp >= 0)//后面还能再接上
{
int now = dfs(to,rest-tmp);//往下搜
if(now == -1)
{
return f[x][rest] = -1;
}
f[x][rest] =(f[x][rest] + now) % p;//f[x][rest]表示从x到n还能比最短路多走rest的方案数
}
}
vis[x][rest] = 0;
return f[x][rest]%p;
}
int main()
{
T = read();
while(T--)
{
chushihua();
n = read(); m = read(); k = read(); p = read();
for(int i = 1; i <= m; i++)
{
u = read(); v = read(); w = read();
add(u,v,w);//建双向边
}
dij();
printf("%d\n",dfs(1,k));
}
return 0;
}